Math in Focus Grade 5 Chapter 13 Answer Key Properties of Triangles and Four-sided Figures

by

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 13 Properties of Triangles and Four-sided Figures provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 13 Answer Key Properties of Triangles and Four-sided Figures

Put On Your Thinking Cap!

Challenging Practice

This figure is a rhombus and ∠ADO = ∠CDO. Find the measure of ∠DOC.
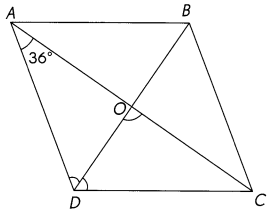
Math in Focus Grade 5 Chapter 13 Answer Key Properties of Triangles and Four-sided Figures 1
Answer:
∠DOC = 90°
Explanation:
The diagonals of a rhombus bisect each other at right angles (90°)
∠DOC = 90°

Put on Your Thinking cap!

Problem Solving

Question 1.
ABCD is a trapezoid in which \(\overline{A D}\) || \(\overline{B C}\). Find the measure of ∠CED.
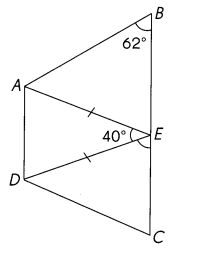
Math in Focus Grade 5 Chapter 13 Answer Key Properties of Triangles and Four-sided Figures 2
Answer:

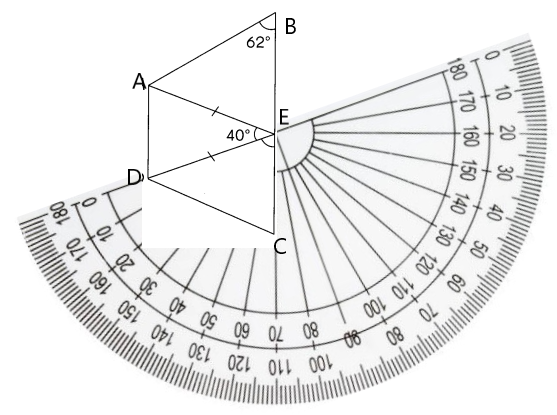
Explanation:
With the help of protractor we find the Measure of ∠CED.
∠CED. = 70°

Question 2.
ABCD is a parallelogram and CDEF is a rhombus. Find the measure of ∠ADE.
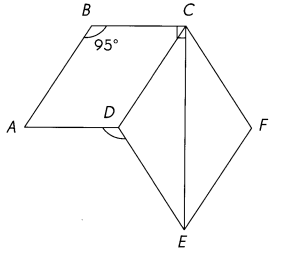
Math in Focus Grade 5 Chapter 13 Answer Key Properties of Triangles and Four-sided Figures 3
Answer:


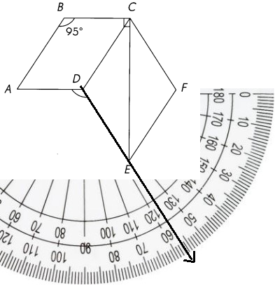
Explanation:
By using the protractor we can find the Angle of ADE
∠ADE. = 137°

Math Journal

Question 1.
A teacher asked her students to sketch and label the angles of a triangle. These are the angle measures that three students chose to draw.
Wayne: 120°, 80°, 10° Ashley: 70°, 28°, 72° Frank: 51 °, 37°, 92°
Will each student be able to draw his or her triangle? Explain your answer.
Wayne: _______
Ashley: ________
Frank: ______
Answer:
Wayne: 120°, 80°, 10° = 210°
Ashley: 70°, 28°, 72° = 170°
Frank: 51 °, 37°, 92° =  180°
Explanation:
The sum of all the angles of an triangle is equal to 180 degrees
Only Frank can draw the triangle.

Question 2.
What are two ways to identify an isosceles triangle?
Answer:
Isosceles. An isosceles triangle can be drawn in many different ways. It can be drawn to have two equal sides and two equal angles or with two acute angles and one obtuse angle.

Question 3.
Jordan is measuring the angles of a triangle. He finds out that m∠A = m∠B = 60°. Without measuring ∠C, he says that triangle ABC is an equilateral triangle. Is he correct? Explain why.
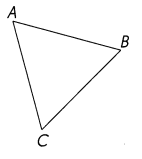
Math in Focus Grade 5 Chapter 13 Practice 1 Answer Key Right, Isosceles, and Equilateral Triangles 26
Explanation:
Yes.
The sum of all the angles of an equilateral triangle is equal to 180 degrees. As all the angles are equal to 60 degrees, the sum is equal to 60°+ 60°+ 60° =180 degrees
m∠C = 60°

Leave a Comment