This handy Math in Focus Grade 4 Workbook Answer Key Chapter 12 Practice 5 Using Formulas for Area and Perimeter detailed solutions for the textbook questions.
Math in Focus Grade 4 Chapter 12 Practice 5 Answer Key Using Formulas for Area and Perimeter
Solve. Show your work.
Example
The floor of a patio measuring 8 feet by 7 feet is tiled with 1 -foot square tiles. The shaded area in the figure is tiled in black, and the unshaded area is tiled in white. What is the area tiled in white?
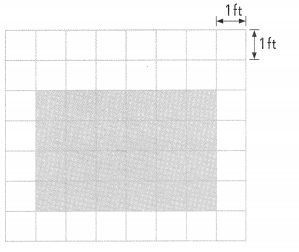
Area of patio = 8 × 7
= 56 ft2
Shaded area = 6 × 4
= 24 ft2
Area of patio – shaded area
= 56 – 24
= 32 ft2
The area tiled in white is 32 square feet.
Question 1.
The floor of Mr. Jones’ living room is in the shape shown below.
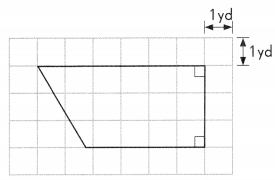
a. Estimate, in square yards, the area of his living room.
Answer:
We can calculate the living rom by making the room into two shapes where area of them can be easily find.
Area of the living room = area of the triangle + area of the rectangle
= 1/2 × 3 × 2 + 4 × 3
= 3 + 12
= 15
The estimated area of Mr. Jones’ living room is 15 square yards.
b. Mr. Jones wants to carpet his living room. If a roll of carpet is 3 yards wide, what is the smallest length of carpet Mr. Jones should buy?
Answer:
Area of the carpet required is 15 square yards.
As carpet will be in rectangular shape, so length x width = 15
As given, width is 3 yards. So 3 × 5 = 15
The smallest length of carpet Mr. Jones should buy is 5 yards.
Solve. Show your work.
Question 2.
The figure shows a small rectangle and a large rectangle. Find the area of the shaded part of the figure.
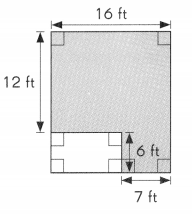
Area of large rectangle = ___________ × ___________
= ______________ ft2
Area of small rectangle = ___________ × ___________
= ________ ft2
Area of shaded part area of large rectangle – area of small rectangle
= ________ ft2
The area of the shaded part is __________ square feet.
Answer:
Area of large rectangle = 18ft × 16ft
= 288 ft2
Area of small rectangle = 9ft × 6ft
= 54 ft2
Area of shaded part area of large rectangle – area of small rectangle
= 288 ft2 – 54 ft2
= 234 ft2
The area of the shaded part is 234 square feet.
Solve. Show your work.
Question 3.
The figure shows a small rectangle and a large rectangle. Find the area of the shaded part of the figure.
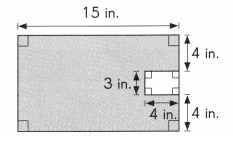
Area of large rectangle = ___________ × ___________
= ______________ in.2
Area of small rectangle = ___________ × ___________
= ________ in.2
Area of shaded part area of large rectangle – area of small rectangle
= ________ in.2
The area of the shaded part is __________ square inches.
Answer:
Area of large rectangle = 15 in × 11 in
= 165 in.2
Area of small rectangle = 4 in × 3 in
= 12 in.2
Area of shaded part area of large rectangle – area of small rectangle
= 165 – 12
=153 in.2
The area of the shaded part is 153 square inches.
Example
A rug is centered on a rectangular floor as shown in the diagram. Find the area of the rug.
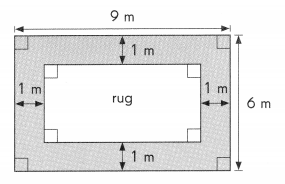
Length of rug = 9 – 1 – 1
= 7 m
Width of rug = 6 – 1 – 1
= 4 m
Area of rug = 7 × 4
= 28 m2
The area of the rug is 28 square meters.
Solve. Show your work.
Question 4.
A rectangular pool is surrounded by a 2-yard-wide deck as shown in the diagram. Find the area of the deck.
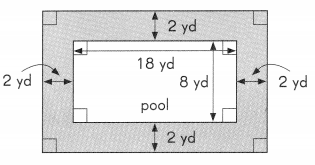
Answer:
Total area = 22yd × 12yd
= 264 yd2
Area of the pool = 18yd × 8yd
= 144 yd2
Area of the deck = Total area – area of the pool
= 264 – 144
= 120 yd2
The area of the deck is 120 square yards.
Question 5.
A rectangular picture frame measures 25 centimeters by 1 5 centimeters. It has a wooden border 3 centimeters wide. To fit the picture frame, how large should a picture be?
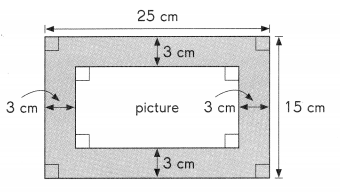
Answer:
Length of picture = 25 – 3 – 3
= 19 cm
Width of picture = 15 – 3 – 3
= 9 m
Area of picture = 19 × 9
= 171 cm2
The area of the picture is 171 square centimeters.
Solve. Show your work.
Question 6.
Renee has a piece of rectangular cardboard measuring 90 centimeters by 80 centimeters. She cuts out a small rectangular piece measuring 15 centimeters by 20 centimeters.
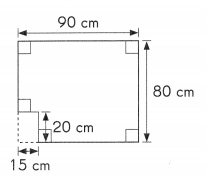
a. Find the area of the remaining piece of cardboard.
Answer:
Area of larger rectangular cardboard = 90 cm × 80 cm = 7,200 cm2
Area of smaller rectangular cardboard = 20 cm × 15 cm = 300 cm2
Area of the remaining piece of cardboard = Area of larger rectangular cardboard – area of smaller rectangular cardboard
= 7,200 – 300
= 6,900 cm2
Area of remaining piece of cardboard is 6,900 square centimeters.
b. Find the perimeter of the remaining piece of cardboard.
Answer:
Even if we remove a rectangular piece of cardboard at the edge of larger cardboard, the perimeter remains same.
Perimeter of larger rectangular cardboard = 90 cm + 80 cm + 90 cm+ 80 cm = 340 cm
Perimeter of remaining piece of cardboard is 340 centimeters.
c. Compare the perimeter of the remaining piece of cardboard with that of the original piece of cardboard. Which one is greater?
Answer:
Perimeter of remaining piece of cardboard is 340 centimeters.
Perimeter of original piece of cardboard is 340 centimeters.
Perimeter of original piece of cardboard is equal to perimeter of remaining piece of cardboard.
Solve. Show your work.
Question 7.
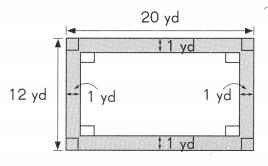
Melanie makes a path 1 yard wide around her rectangular patch of land as shown in the diagram. Find the perimeter and area of the patch of land.
Answer:
Length of patch of land = 20 – 1 – 1
= 18 yards
Width of patch of land = 12 – 1 – 1
= 10 yards
Area of patch of land = 18 × 10
= 180 yd2
The area of the patch of land is 180 square yards.
Perimeter of the patch of land = 18 + 10 + 18 + 10
= 56 yards
Question 8.
A rectangular piece of paper measuring 15 centimeters by 7 centimeters is folded along the dotted lines to form the figure shown.
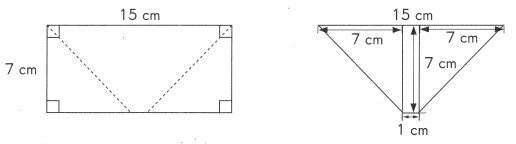
Find the area of the figure formed.
Answer:
Area of the triangle = 1/2 × b × h
= 1/2 × 7 × 7
= 49/2 square centimeters
Area of the rectangle = length × width
= 7 cm × 1 cm
= 7 square centimeters
Area of the triangle = 1/2 × b × h
= 1/2 × 7 × 7
= 49/2 square centimeters
Area of the figure = Area of the triangle + Area of the rectangle + Area of the triangle
= 49/2 + 7 + 49/2
= 56 square centimeters
Area of the figure formed is 56 square centimeters