This handy Math in Focus Grade 4 Workbook Answer Key Chapter 12 Area and Perimeter detailed solutions for the textbook questions.
Math in Focus Grade 4 Chapter 12 Answer Key Area and Perimeter
Math Journal
Look at John’s answers for the area and perimeter of the figures.
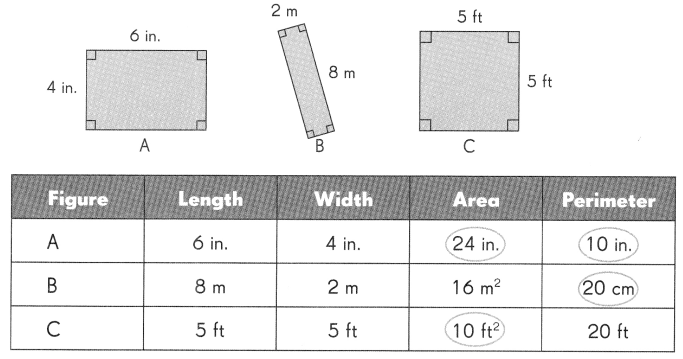
John’s mistakes are circled.
Explain why these answers are wrong. Write the correct answers.
Example
Area of figure A: The unit for the area of figure A should be ‘in.2‘.
Question 1.
Perimeter of figure A: _____________
Answer:
Length = 6 in
width = 4 in
Perimeter of figure A = 2 (l + w)
= 2(6 + 4)
= 2 (10)
= 20 in
Perimeter of figure A should be 20 inches.
Question 2.
Perimeter of figure B: _____________
Answer:
Length = 8 m
width = 2 m
Perimeter of figure B = 2 (l + w)
= 2(8 + 2)
= 2 (10)
= 20 m
The unit for the perimeter of the figure B should be ‘m’.
Question 3.
Area of figure C: ________________
Answer:
Length = 5 feet
width = 5 feet
Area of figure C = l x w
= 5 feet x 5 feet
= 20 square feet
Area of figure C should be 25 square feet.
Put On Your Thinking Cap!
Challenging Practice
Question 1.
Using the gridlines, draw as many different rectangles as you can that have an area of 12 square centimeters. Do the same for rectangles with an area of 9 square centimeters. How many rectangles can you draw for each area?

Answer:
Solve. Show your work.
Question 2.
The length of a painting is 3 times its width, Its perimeter is 64 inches. Find the length.
Answer:
The length of a painting is 3 times its width
l = 3w
Its perimeter is 64 inches.
perimeter of a painting = 2 (l + w)
64 inches = 2(3w + w)
64 inches = 8w
8 inches = w
length = 3 x w
= 3 x 8 inches
length = 24 inches
Question 3.
The length of a dog run is twice its width. Its area is 50 square yards. Find the length and width of the dog run.
Answer:
The length of a dog run is twice its width.
l = 2w
Its area is 50 square yards.
Area = length x width
50 square yards = 2w × w
25 yd2 =w2
5 yards = w
Width of the dog run is 5 yards.
Length = 2 × w
length = 2 × 5
length = 10 yards
length of the dog run is 10 yards.
Solve. Show your work.
Question 4.
A rectangular garden measuring 15 meters by 8 meters is bordered by a house on one side as shown. How much fencing material is needed for the garden?
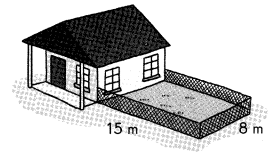
Answer:
A rectangular garden measuring 15 meters by 8 meters is bordered by a house on one side as we can observe in the above figure.
Fencing material needed for the garden = 15 m + 8 m + 15 m = 38 m
The fencing material needed for the garden is 38 m.
Question 5.
Mrs. Evan covered the rectangular floor of her living room with a parallelogram-shaped carpet as shown. The floor measures 5 feet by 7 feet. How much of the floor is covered with carpet?
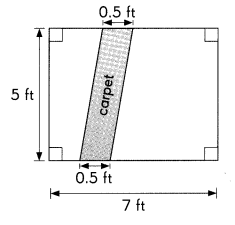
Answer:
Estimate the area.
Question 6.
Peter wanted to make a collage of a park. How much paper would he need to make this pond?
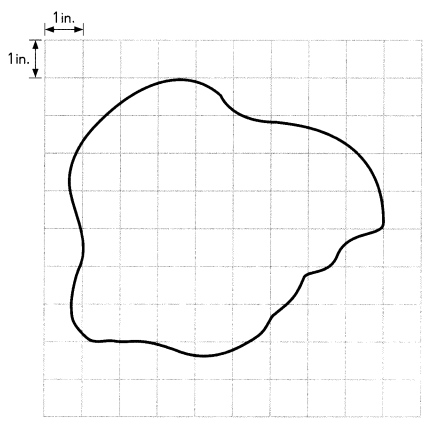
Answer:
He need 40 inches to make the above pond.
Put On Your Thinking Cap!
Problem Solving
Question 1.
Shawn has a piece of cardboard as shown in the diagram. He wants to cut out as many squares as possible from the cardboard. How many squares can he cut if each side of a square is
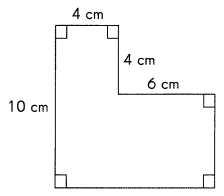
(a) 2 centimeters long?
(b) 3 centimeters long?
(c) 4 centimeters long?
Answer:
a.
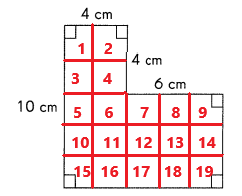
If each side of a square is 2 centimeters long he can cut 19 squares.
b.
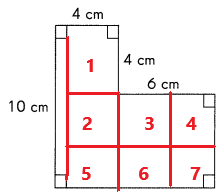
If each side of a square is 3 centimeters long he can cut 7 squares.
c.
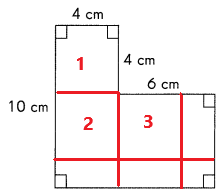
If each side of a square is 4 centimeters long he can cut 4 squares.
Question 2.
Figure A shows a piece of paper folded to form a square with 8-inch sides as shown in the diagram. Figure B shows one of the flaps opened. Find the area of figure B.
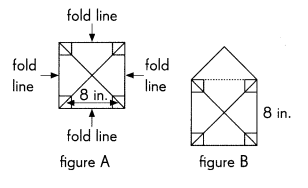
Answer:
Area of the square = side × side
= 8 in × 8 in
= 64 square inches
Area of the triangle = 1/2 × b × h
= 1/2 × 8 in × 4 in
= 16 square inches
Area of figure B = Area of a square + Area of triangle
= 64 in2+ 16 in2
= 80 in2
Area of figure B is 80 square inches.
Solve. Show your work.
Question 3.
The figure shows two squares. The area of the unshaded part of the figure is 9 square feet. If the sides of both the squares are whole numbers, find the perimeter of the unshaded part.

Answer: