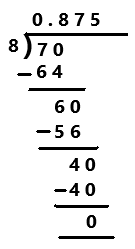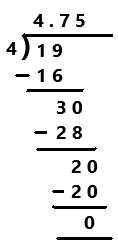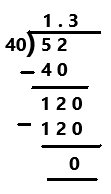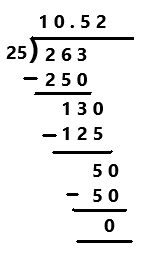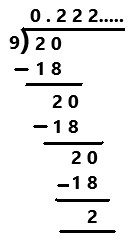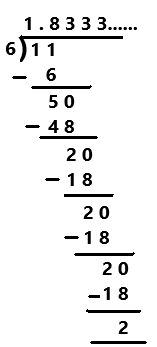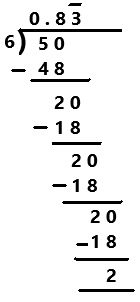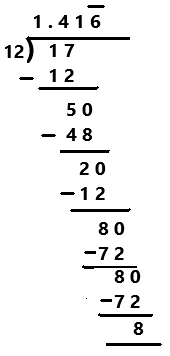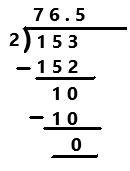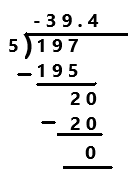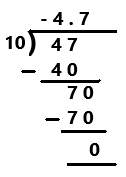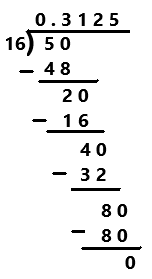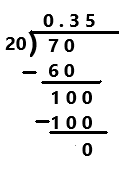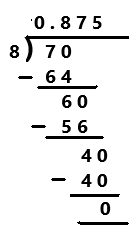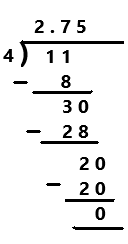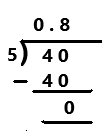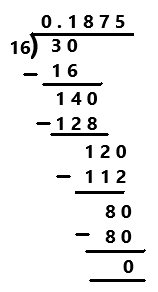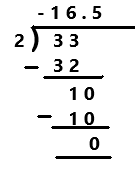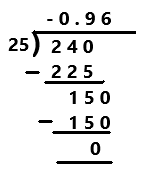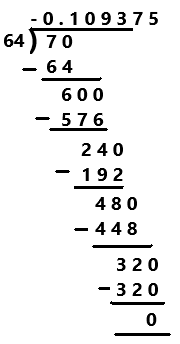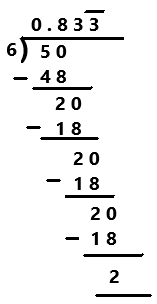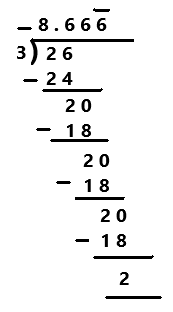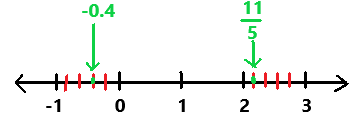Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.2 Writing Rational Numbers as Decimals to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.2 Answer Key Writing Rational Numbers as Decimals
Math in Focus Grade 7 Chapter 1 Lesson 1.2 Guided Practice Answer Key
Using long division, write each rational number as a terminating decimal.
Question 1.
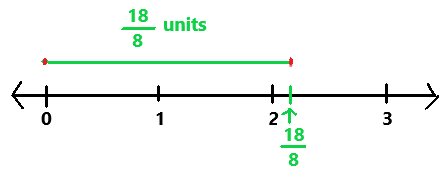
\(\frac{7}{8}\)
Answer:
7/8
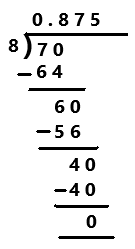
Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. By using long division divide 7 by 8 the quotient is 0.875 which is a terminating decimal.
Question 2.
\(\frac{19}{4}\)
Answer:
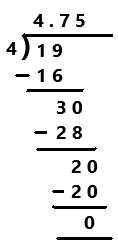
Explanation:
Perform division operation on given rational number. By using long division divide 19 by 4 the quotient is 4.75 which is a terminating decimal.
Question 3.
\(\frac{52}{40}\)
Answer:
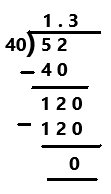
Explanation:
Perform division operation on given rational number. By using long division divide 52 by 40 the quotient is 1.3 which is a terminating decimal.
Question 4.
10\(\frac{13}{25}\)
Answer:
10(13/25)
= (250 + 13)/25
= 263/25
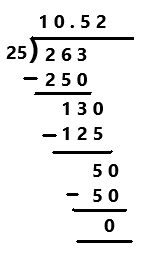
Explanation:
Perform division operation on given rational number. The mixed fraction 10(13/25) in fraction form as 263/25. By using long division divide 263 by 25 the quotient is 10.52 which is a terminating decimal.
Using long division, write each rational number as a repeating decimal.
Question 5.
\(\frac{2}{9}\)
Answer:
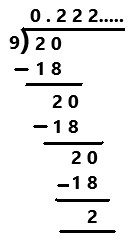
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero. Perform division operation on given rational number. By using long division divide 2 by 9 the quotient is 0.222… which is a repeating decimal.
Question 6.
\(\frac{11}{6}\)
Answer:
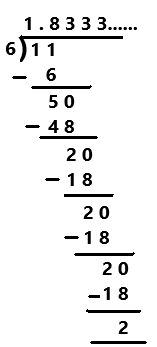
Explanation:
A repeating decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero. Perform division operation on given rational number. By using long division divide 11 by 6 the quotient is 1.8333… which is a repeating decimal.
Using a calculator, write each rational number as a repeating decimal.
Question 7.
\(\frac{23}{24}\)
Answer:
23/24
= 0.958333…
Explanation:
Perform division operation on given rational number. By using calculator divide 23 by 24 the quotient is 0.958333… which is a repeating decimal.
Question 8.
\(\frac{78}{37}\)
Answer:
78/37
= 2.108108….
Explanation:
Perform division operation on given rational number. By using calculator divide 78 by 37 the quotient is 2.108108… which is a repeating decimal.
Using long division, write each rational number as a repeating decimal. Use bar notation to indicate the repeating digits.
Question 9.
\(\frac{5}{6}\)
Answer:
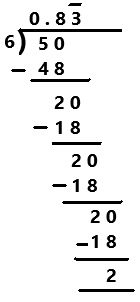
Explanation:
Perform division operation on given rational number. By using long division divide 5 by 6 the quotient is 0.8333… which is a repeating decimal. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above image.
Question 10.
\(\frac{17}{12}\)
Answer:
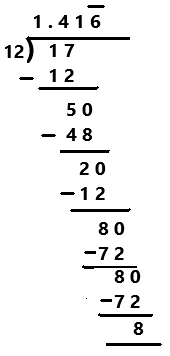
Explanation:
Perform division operation on given rational number. By using long division divide 17 by 12 the quotient is 1.41666… which is a repeating decimal. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above image.
Technology Activity
Materials:
Classify rational numbers in decimal form
Work in pairs.
Step 1.
On a spreadsheet, label four columns with the following column heads.

Step 2.
Enter each rational number below in the first column, labeled “Rational Numbers in Decimal Form”. Make sure that the cells in this column are formatted to display decimals up to 8 decimal places.
\(\frac{5}{16}\), \(\frac{141}{25}\), –\(\frac{40}{111}\), –\(\frac{15}{16}\), \(\frac{14}{5}\), \(\frac{1}{8}\), –\(\frac{9}{44}\), \(\frac{2}{11}\), \(\frac{5}{4}\) and –\(\frac{40}{9}\).
For example, if you enter into the spreadsheet, the entry will show the decimal form of this fraction.
Step 3.
Determine whether the decimal ¡s terminating, repeating, or neither. Enter either “Terminating”, “Repeating”, or “Neither” in the second column.
Step 4.
If the decimal terminates, record the number of decimal digits in the third column. If the decimal repeats, record the repeating digits in the fourth column.
Example:

Math Journal
Did you find any decimals that neither terminated nor repeated? What can you conclude about the decimal form of a rational number?
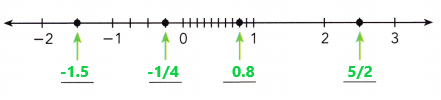
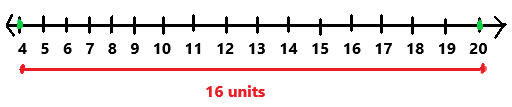
Compare the positive rational numbers using the symbols < or >. Use a number line to help you.
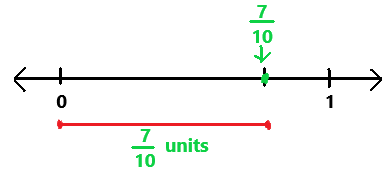
Question 11.
\(\frac{7}{10}\) ? \(\frac{13}{16}\)
Answer:
7/10 < 13/16
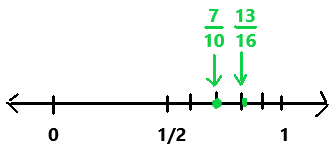
Explanation:
In the above number line we can observe the given positive rational numbers. The positive rational number 7/10 is less than 13/16.
Question 12.
\(\frac{24}{7}\) ? \(\frac{10}{3}\)
Answer:
24/7 > 10/3
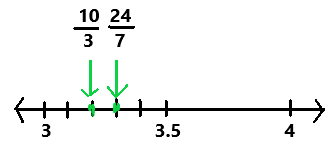
Explanation:
In the above number line we can observe the given positive rational numbers 24/7 and 10/3. The positive rational number 24/7 is greater than 10/3.
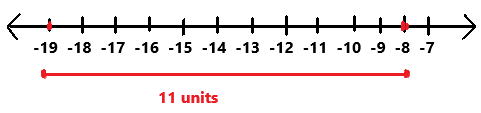
Compare the negative rational numbers using the symbols < or >. Use a number line to help you.
Question 13.
–\(\frac{3}{5}\) ? –\(\frac{4}{5}\)
Answer:
-3/5 > -4/5
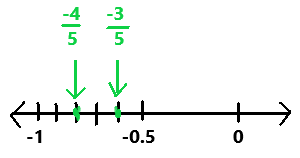
Explanation:
In the above number line we can observe the given negative rational numbers -3/5 and -4/5. The negative rational number -3/5 is greater than -4/5.
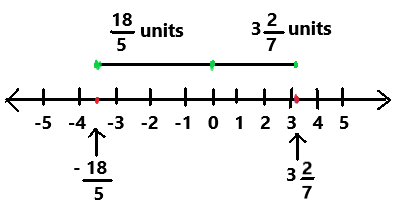
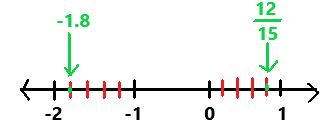
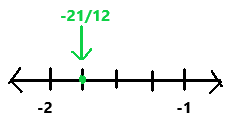
Question 14.
-10\(\frac{3}{4}\) ? –\(\frac{41}{5}\)
Answer:
-10(3/4)
= -(40 + 3)/4
= -43/4
-10(3/4) < – 41/5
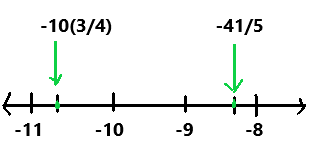
Explanation:
In the above number line we can observe the given negative rational numbers -10(3/4) and -41/5. The negative rational number -10(3/4) is less than -41/5.
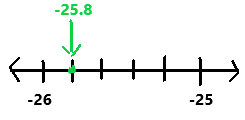
Question 15.
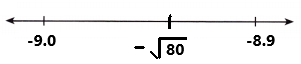
-4.063 ? -4\(\frac{1}{6}\)
Answer:
-4(1/6)
= – (24 + 1)/6
= -25/6
-4.063 > -4(1/6)
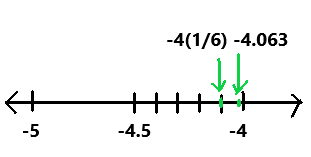
In the above number line we can observe the given negative rational numbers -4.063 and -4(1/6). The negative rational number -4.063 is greater than -4(1/6).
Math in Focus Course 2A Practice 1.2 Answer Key
Using long division, write each rational number as a terminating decimal.
Question 1.
76\(\frac{1}{2}\)
Answer:
76(1/2)
= 153/2
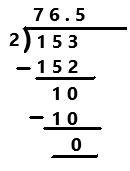
Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. The mixed fraction 76(1/2) in fraction form is 153/2. By using long division divide 153 by 2 the quotient is 76.5 which is a terminating decimal.
Question 2.
-39\(\frac{2}{5}\)
Answer:
-39(2/5)
= -(195 + 2)/5
= -197/5
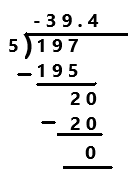
Explanation:
Perform division operation on given rational number. The mixed fraction -39(2/5) in fraction form is -197/5. By using long division divide -197 by 5 the quotient is -39.4 which is a terminating decimal.
Question 3.
–\(\frac{47}{10}\)
Answer:
-47/10
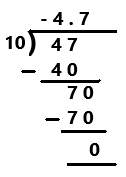
Explanation:
Perform division operation on given rational number. By using long division divide -47 by 10 the quotient is -4.7 which is a terminating decimal.
Question 4.
\(\frac{5}{16}\)
Answer:
5/16
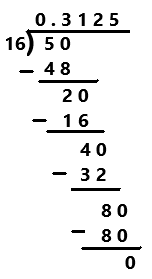
Explanation:
Perform division operation on given rational number. By using long division divide 5 by 16 the quotient is 0.3125 which is a terminating decimal.
Question 5.
\(\frac{7}{20}\)
Answer:
7/20
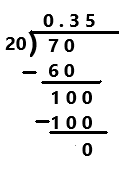
Explanation:
Perform division operation on given rational number. By using long division divide 7 by 20 the quotient is 0.35 which is a terminating decimal.
Question 6.
\(\frac{7}{8}\)
Answer:
7/8
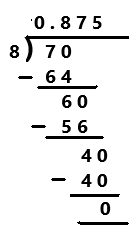
Explanation:
Perform division operation on given rational number. By using long division divide 7 by 8 the quotient is 0.875 which is a terminating decimal.
Simplify each rational number. Then use long division to write each rational number as a terminating decimal.
Question 7.
\(\frac{99}{36}\)
Answer:
99/36
= 11/4
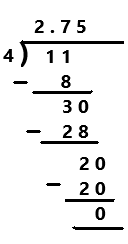
Explanation:
The given ration number is 99/36. The simplified form of a given rational number is 11/4. Perform division operation on simplified rational number. By using long division divide 11 by 4 the quotient is 2.75 which is a terminating decimal.
Question 8.
\(\frac{12}{15}\)
Answer:
12/15
= 4/5
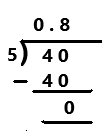
Explanation:
The given ration number is 12/15. The simplified form of a given rational number is 4/5. Perform division operation on simplified rational number. By using long division divide 4 by 5 the quotient is 0.8 which is a terminating decimal.
Question 9.
\(\frac{9}{48}\)
Answer:
9/48
= 3/16
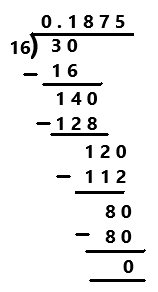
Explanation:
The given ration number is 9/48. The simplified form of a given rational number is 3/16. Perform division operation on simplified rational number. By using long division divide 3 by 16 the quotient is 0.1875 which is a terminating decimal.
Question 10.
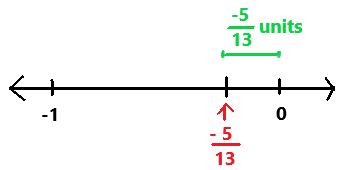
–\(\frac{132}{8}\)
Answer:
-132/8
= -33/2
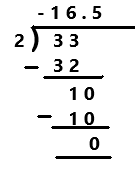
Explanation:
The given ration number is -132/8. The simplified form of a given rational number is -33/2. Perform division operation on simplified rational number. By using long division divide -33 by 2 the quotient is -16.5 which is a terminating decimal.
Question 11.
–\(\frac{48}{50}\)
Answer:
-48/50
= -24/25
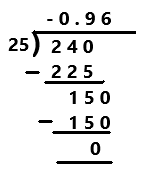
Explanation:
The given ration number is -48/50. The simplified form of a given rational number is -24/25. Perform division operation on simplified rational number. By using long division divide -24 by 25 the quotient is -0.96 which is a terminating decimal.
Question 12.
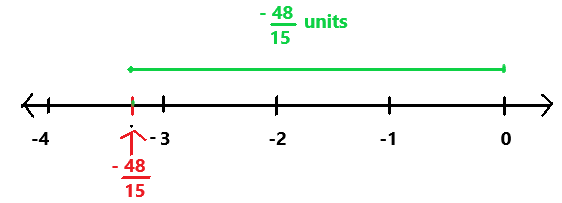
–\(\frac{14}{128}\)
Answer:
-14/128
= -7/64
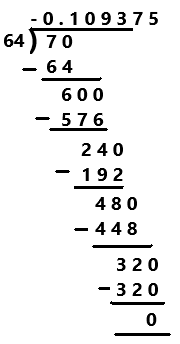
Explanation:
The given ration number is -14/128. The simplified form of a given rational number is -7/64. Perform division operation on simplified rational number. By using long division divide -7 by 64 the quotient is -0.109375 which is a terminating decimal.
Using long division, write each rational number as a repeating decimal with 3 decimal places. Identify the pattern of repeating digits using bar notation.
Question 13.
\(\frac{5}{6}\)
Answer:
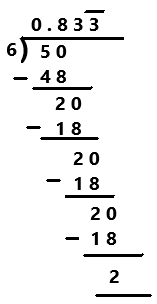
Explanation:
Perform division operation on given rational number. By using long division divide 5 by 6 the quotient is 0.83333… which is a repeating decimal. The repeating decimal with 3 decimal places is denoted as 0.833 bar for the number 3 on last. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above image.
Question 14.
-8\(\frac{2}{3}\)
Answer:
-8(2/3)
= -(24+2)/3
= -26/3
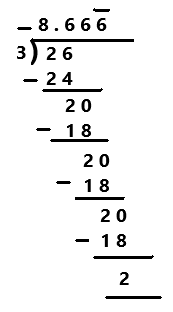
Explanation:
The mixed fraction -8(2/3) in fraction form is -26/3. Perform division operation on fraction. By using long division divide -26 by 3 the quotient is -8.66666… which is a repeating decimal. The repeating decimal with 3 decimal places is denoted as -8.666 bar for the number 6 on last. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above image.
Write each rational number as a repeating decimal using bar notation. You may use a calculator.
Question 15.
\(\frac{8}{55}\)
Answer:
8/55
= 0.1454545…
= 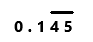
Explanation:
Perform division operation on given rational number. By using calculator divide 8 by 55 the quotient is 0.1454545… which is a repeating decimal. The repeating decimal 45 is represented by bar notation as we can observe in the answer.
Question 16.
\(\frac{456}{123}\)
Answer:
456/123
= 3.7073170731….
= 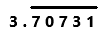
Explanation:
Perform division operation on given rational number. By using calculator divide 456 by 123 the quotient is 3.7073170731… which is a repeating decimal. The repeating decimal 70731 is represented by bar notation as we can observe in the answer.
Question 17.
–\(\frac{987}{110}\)
Answer:
-987/110
= -8.9727272….
= 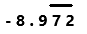
Explanation:
Perform division operation on given rational number. By using calculator divide -987 by 110 the quotient is -8.9727272… which is a repeating decimal. The repeating decimal 72 is represented by bar notation as we can observe in the answer.
Question 18.
\(\frac{11}{14}\)
Answer:
11/14
= 0. 7857142857142….
= 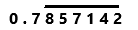
Explanation:
Perform division operation on given rational number. By using calculator divide 11 by 14 the quotient is 0.7857142857142… which is a repeating decimal. The repeating decimal 857142 is represented by bar notation as we can observe in the answer.
Question 19.
–\(\frac{10}{13}\)
Answer:
-10/ 13
= – 0. 769230769230….
= 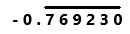
Explanation:
Perform division operation on given rational number. By using calculator divide -10 by 13 the quotient is -0.769230769230… which is a repeating decimal. The repeating decimal 769230 is represented by bar notation as we can observe in the answer.
Question 20.
\(\frac{4,005}{101}\)
Answer:
4,005/101
= 39.65346534….
= 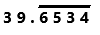
Explanation:
Perform division operation on given rational number. By using calculator divide 4,005 by 101 the quotient is 39.65346534… which is a repeating decimal. The repeating decimal 6534 is represented by bar notation as we can observe in the answer.
Refer to the list of rational numbers below for questions 21 to 23, You may use a calculator.
–\(\frac{23}{32}\), \(\frac{7}{15}\), –\(\frac{368}{501}\), –\(\frac{19}{26}\), \(\frac{37}{44}\)
Question 21.
Write each rational number as a decimal with at most 6 decimal places.
Answer:
Given rational numbers are -23/32, 7/15, -368/501, -19/26, 37/44.
The given rational numbers in a decimal form with at most 6 decimal places.
-0.71875, 0.466667, -0.734531, -0.730769, 0.840909
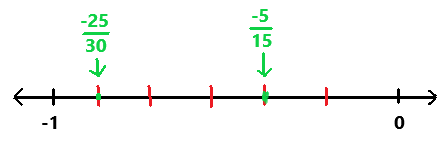
Question 22.
Using your answers in 21 list the numbers from least to greatest using the symbol <. Graph a number line between —1 and 1 with 0 in the middle. Then, place each rational number on the number line.
Answer:
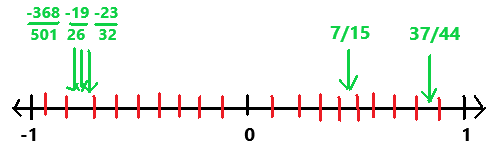
Explanation:
From the answer 21 the numbers from least to greatest are -368/501, -19/26, -23/32, 7/15, 37/44. In the above image we can observe the above given rational numbers on the number line.
Question 23.
Math Journal Margo tries to compare –\(\frac{2}{3}\) and –\(\frac{5}{8}\) using absolute values. She finds their decimal equivalents to be –\(0 . \overline{6}\) and —0.625, and she knows |-\(0 . \overline{6}\)| |-0.625|. Explain why she must reverse the inequality in her final answer, –\(\frac{2}{3}\) < –\(\frac{5}{8}\)
Answer:
The greater the absolute value of a number the farther that number is from 0.
So, -2/3 is farther to the left of 0 than -5/8.
A number that is to the left of another number on the number line is less than that number. So, -2/3 < -5/8.


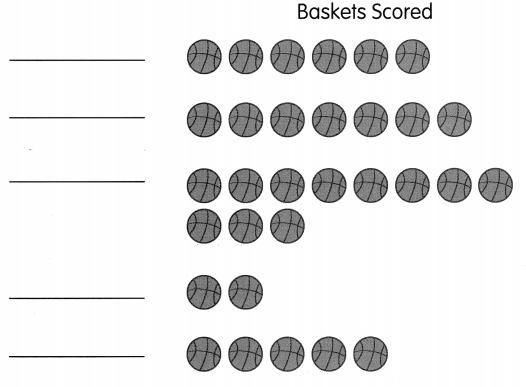
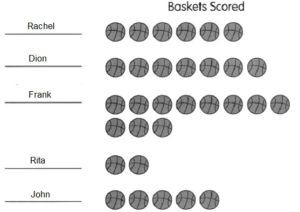


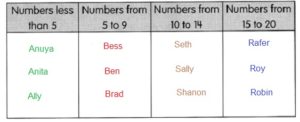


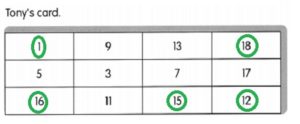





![]()






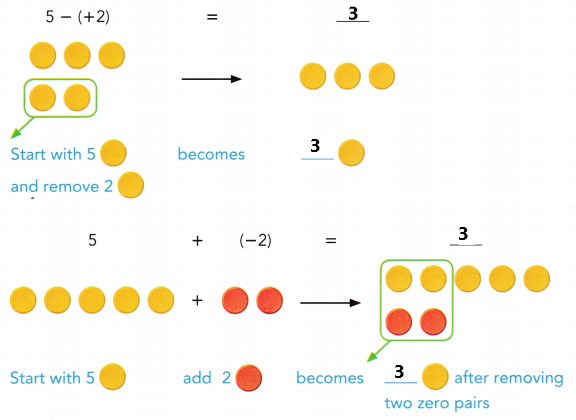
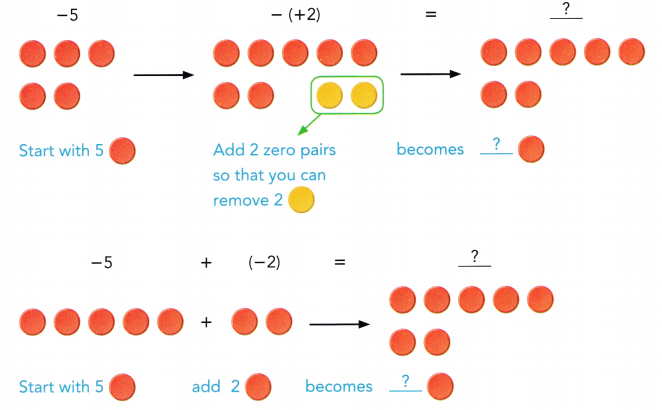
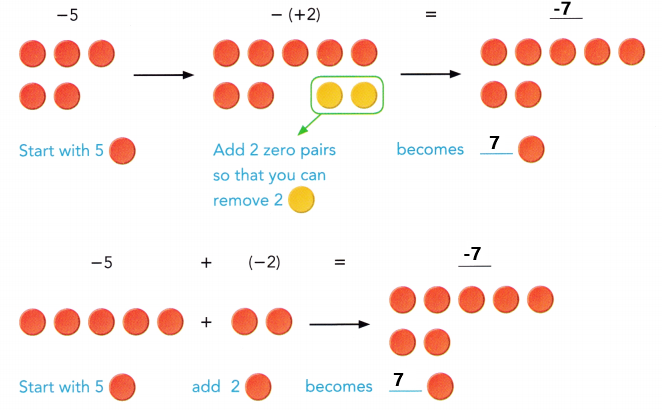
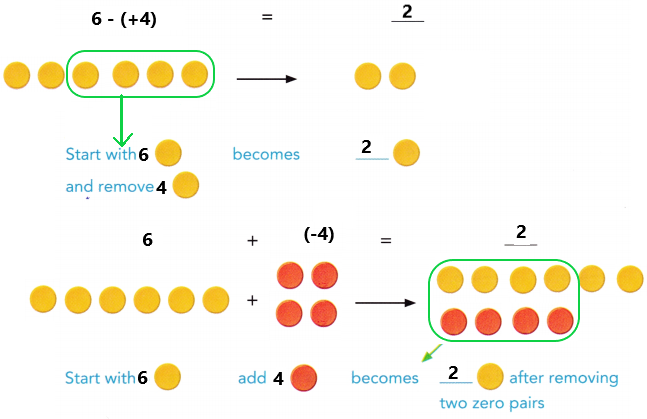
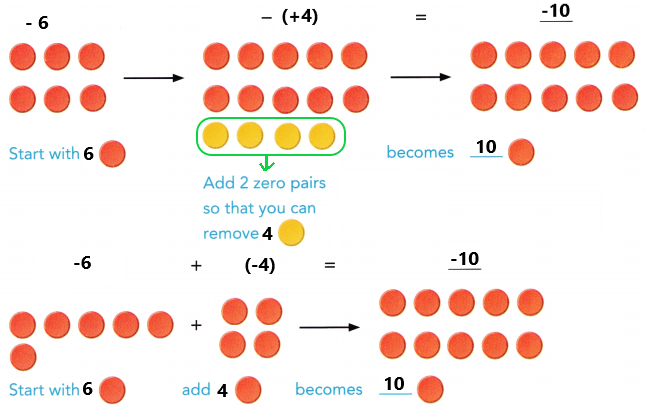
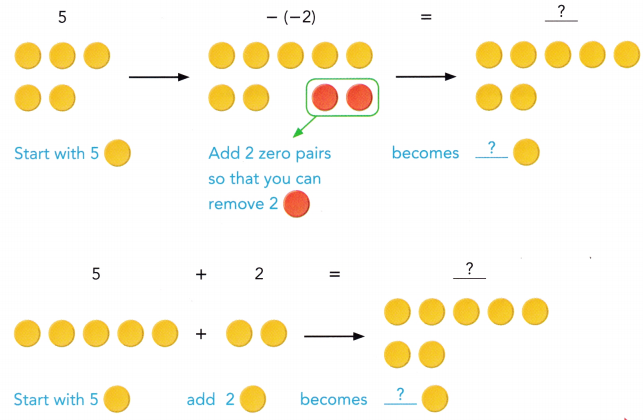
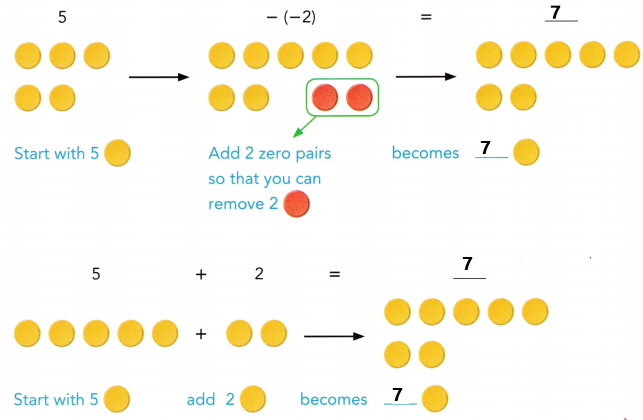
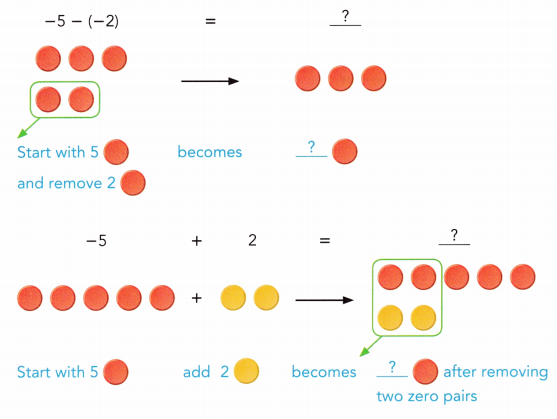
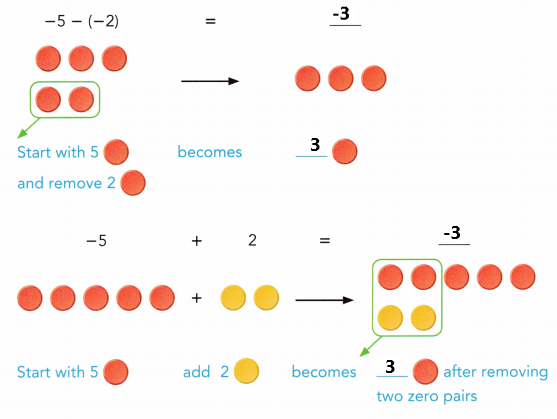
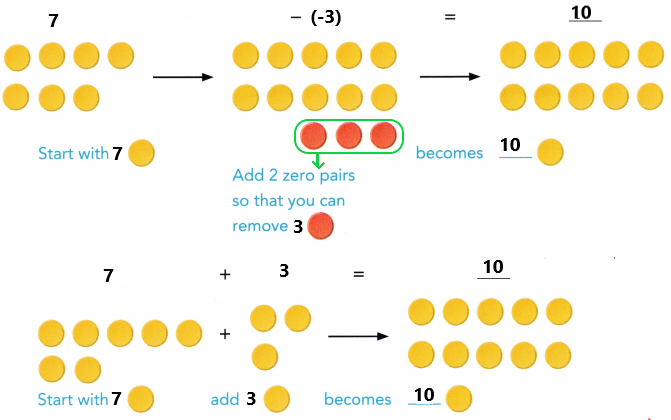
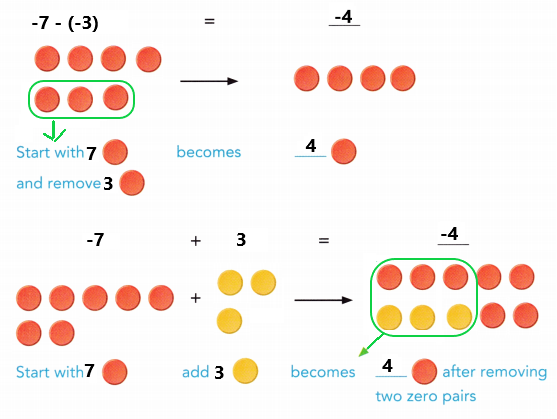







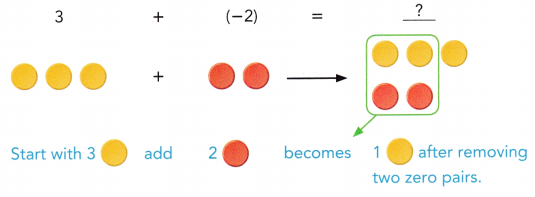
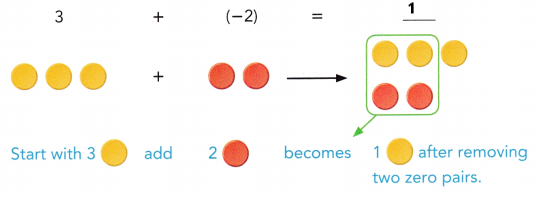
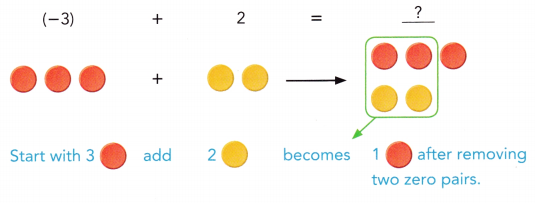
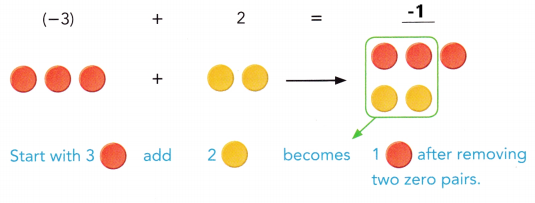
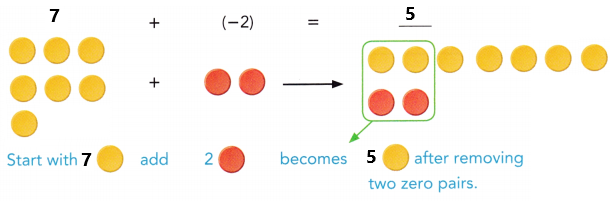
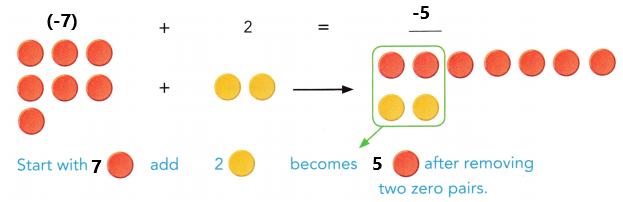
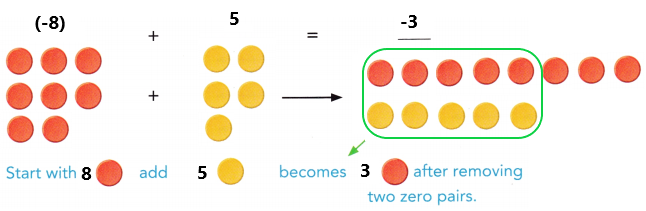
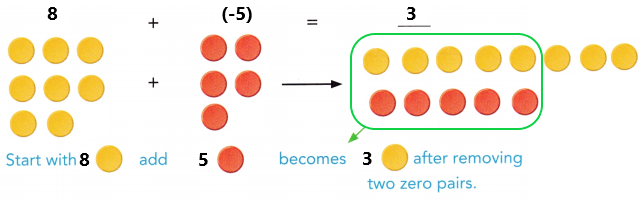

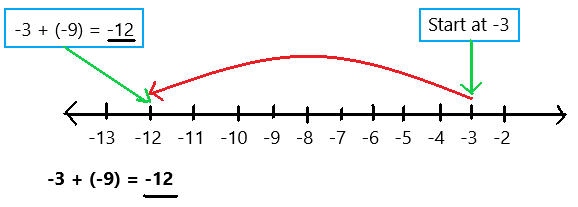
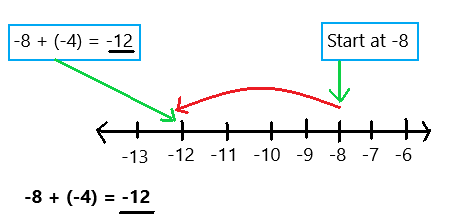
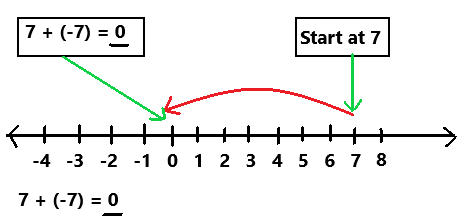
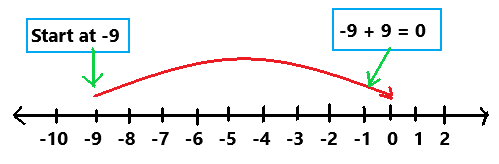
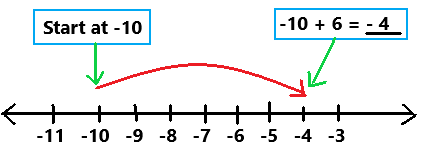
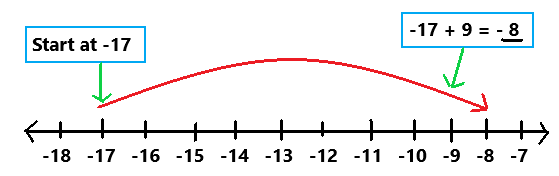
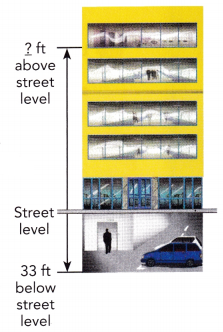
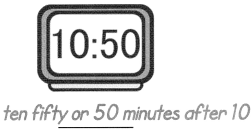








 are examples of _____________.
are examples of _____________.