Hillary

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 2 Practice 5 Addition with Regrouping in Tens to finish your assignments.

Math in Focus Grade 2 Chapter 2 Practice 5 Answer Key Addition with Regrouping in Tens

Add and regroup the tens.

Question 1.
534 + 283 = ?
Add the ones.
4 ones + 3 ones = ones
Add and regroup the tens.
3 tens + 8 tens = ___ tens

= ___ hundred ___ ten
Add the hundreds.
1 hundred + 5 hundreds + 2 hundreds = ___ hundreds
534 + 283 = ____
Answer:
534 + 283 = 817
Explanation:
4 ones + 3 ones = 7 ones
Add and regroup the tens.
3 tens + 8 tens = 11 tens
= 1 hundred 1 ten
Add the hundreds.
1 hundred + 5 hundreds + 2 hundreds = 8 hundreds

Question 2.

Answer:

Explanation:
2  ones + 5 ones = 7 ones
Add and regroup the tens.
6 tens + 7 tens = 13 tens
= 1 hundred 3 ten
Add the hundreds.
1 hundred + 4 hundreds + 1 hundreds = 6 hundreds

Question 3.

Answer:

Explanation:
8 ones + 1 ones = 9 ones
Add and regroup the tens.
4  tens + 6 tens = 10 tens
= 1 hundred 0 ten
Add the hundreds.
1 hundred + 6 hundreds + 1 hundreds = 8 hundreds

Question 4.
295 + 633 = ___

Answer:

Explanation:
5 ones + 3 ones = 8 ones
Add and regroup the tens.
9 tens + 3  tens = 12 tens
= 1 hundred 2 ten
Add the hundreds.
1 hundred + 2 hundreds + 6 hundreds = 9 hundreds

Question 5.
462 + 456 = ___

Answer:

Explanation:
2 ones + 6 ones = 8 ones
Add and regroup the tens.
6 tens + 5 tens = 11 tens
= 1 hundred 1 ten
Add the hundreds.
1 hundred + 4 hundreds + 4 hundreds = 9 hundreds

Add.

Question 6.

Answer:

Kim lost her robots.
Her robots have the same answer.
To help her find her robots, color the robots with the same answer.
Explanation:
no matches were found
for Kim’s lost robots.

This handy Math in Focus Grade 1 Workbook Answer Key Cumulative Review Chapters 3 and 4 detailed solutions for the textbook questions.

Math in Focus Grade 1 Cumulative Review Chapters 3 and 4 Answer Key

Concepts and Skills

Look at the pictures. Complete the number sentences.

Question 1.

Answer:

Explanation:
8 breads are colored and baked 2 breads are not colored and baked
so, total number of breads baked are = 8 + 2 = 10

Question 2.

Answer:

Explanation:
In a ten frame there are 9 dots in that 4 are crossed
so, 9 – 4 = 5

Complete the number bonds. Fill in the blanks.

Question 3.
___ + 5 = 10

Answer:

Explanation:
The sum of 5 and 5 is 10
that is stated by number bond

Question 4.
8 – 3 = ___

Answer:

Explanation:
The difference of 8 and 3 is 4
that is stated by number bond

Fill in the blanks.

Question 5.
2 more than 8 is ____
Answer:
10
Explanation:
2 more than 8 is number 10
2 + 8 = 10

Question 6.
3 less than 7 is ___.
Answer:
4
Explanation:
3 less than 7 is number 4
7 – 3 = 4

Question 7.
_______ is 2 more than 5.
Answer:
7
Explanation:
2 + 5 = 7
number 7 is 2 more than 5.

Question 8.
________ is 5 less than 10.
Answer:
5
Explanation:
10 – 5 = 5
number 5 is 5 less than 10.

Find the missing number.
Use related facts to help you.

Question 9.
2 + ______ = 8
Answer:
6
Explanation:
The sum of 2 and 6 is 8
2 + 6 = 8

Question 10.
______ – 6 = 0
Answer:
6
Explanation:
6 – 6 = 0
The difference of 6 and 6 is 0

Pick three numbers and make a fact family.

Question 11.

Answer:

Explanation:

Problem Solving
Look at the pictures.
Write an addition or subtraction story.

Question 12.

Answer:

Explanation:
There are different shapes of buttons
in them 5 are colored and 4 are non colored
so, total number of buttons are 9
5 + 4 = 9

Question 13.

Answer:

Explanation:
Jamel is catching 9 balloons
3 flew away
so, 9 – 3 = 6
6 are left.

Solve.

Write addition or subtraction sentences.

Question 14.
Ellen has 3 spoons. Her sister gives her 5 spoons. How many spoons does Ellen have now?

Ellen has ___ spoons now.
Answer:

Explanation:
Ellen has 3 spoons. Her sister gives her 5 spoons.
Ellen has 8 spoons now.
3 + 5 = 8

Question 15.
There are 8 fish in a fish tank. 6 are angelfish and the rest are goldfish. How many goldfish are there?

There are ___ goldfish.
Answer:

Explanation:
There are 8 fish in a fish tank. 6 are angelfish and the rest are goldfish.
8 – 6 = 2
There are 2 goldfish.

Go through the Math in Focus Grade 1 Workbook Answer Key Chapter 16 Practice 3 Comparing, Ordering, and Patterns to finish your assignments.

Math in Focus Grade 1 Chapter 16 Practice 3 Answer Key Comparing, Ordering, and Patterns

Find the missing numbers.

Example

2 more than 50 is 52.
2 less than 66 is 64.

Question 1.
2 more than 54 is ____________.
Answer:
2 more than 54 is 56.

Explanation:
Given that 2 more than 54 which is 54+2 = 56.

Question 2.
______________ is 2 more than 66.
Answer:
68 is 2 more than 66.

Explanation:
Given that 2 more than 66 which is 66+2 = 68.

Question 3.
2 less than 78 is ______________.
Answer:
2 less than 78 is 76.

Explanation:
Given that 2 less than 78 which is 78-2 = 76.

Question 4.
____________ is 2 less than 74.
Answer:
72 is 2 less than 74.

Explanation:
Given that 2 less than 74 which is 74-2 = 72.

Question 5.
5 more than 50 is ______________.
Answer:
5 more than 50 is 55.

Explanation:
Given that 5 more than 50 which is 50+5 = 55.

Question 6.
10 more than 85 is ______________.
Answer:
10 more than 85 is 95.

Explanation:
Given that 10 more than 85 which is 95.

Question 7.
5 less than 65 is ______________.
Answer:
5 less than 65 is 60.

Explanation:
Given that 5 less than 65 which is 65-5 = 60.

Question 8.
____________ is 10 less than 100.
Answer:
10 less than 100 is 90.

Explanation:
Given that 10 less than 100 which is 100-10 = 90.

Question 9.
____________ is 5 more than 75.
Answer:
5 more than 75 is 80.

Explanation:
Given that 5 more than 75 which is 80.

Question 10.
____________ is 5 less than 75.
Answer:
5 less than 75 is 70.

Explanation:
Given that 5 is less than 75 which is 70.

Circle the greatest number.

Question 11.
72 or 87
Answer:
87.

Explanation:
Given numbers are 72 and 87. So the greatest number is 87.

Question 12.
92 or 69
Answer:
92.

Explanation:
Given numbers are 92 and 69. So the greatest number is 92.

Question 13.
54 or 45
Answer:
54.

Explanation:
Given numbers are 54 and 45. So the greatest number is 54.

Question 14.
67 or 76
Answer:
76.

Explanation:
Given numbers are 67 and 76. So the greatest number is 76.

Question 15.
86 or 83
Answer:
86.

Explanation:
Given numbers are 86 and 83. So the greatest number is 86.

Question 16.
94 or 98
Answer:
98.

Explanation:
Given numbers are 94 and 98. So the greatest number is 98.

Color the number that is less.

Question 17.

Answer:
59 is less than 71.

Explanation:
Given numbers are 59 and 71. The number 59 is less than 71.

Question 18.

Answer:
68 is less than 93.

Explanation:
Given numbers are 68 and 93. The number 68 is less than 93.

Question 19.

Answer:
79 is less than 97.

Explanation:
Given numbers are 79 and 97. The number 79 is less than 97.

Question 20.

Answer:
48 is less than 48.

Explanation:
Given numbers are 84 and 48. The number 48 is less than 84.

Question 21.

Answer:
62 is less than 67.

Explanation:
Given numbers are 62 and 67. The number 62 is less than 67.

Question 22.

Answer:

Explanation:
Given numbers are 96 and 91. The number 91 is less than 96.

Compare the numbers. Then fill in the blanks.

Question 23.

The least number is ___________.
The greatest number is __________.
Answer:
The least number is 49.
The greatest number is 72.

Explanation:
In the above image, the least number is 49 and the greatest number is 72.

Question 24.

The least number is ___________.
The greatest number is __________.
Answer:
The least number is 69.
The greatest number is 90.

Explanation:
In the above image, the least number is 69 and the greatest number is 90.

Question 25.
Order the numbers from greatest to least.

Answer:
99,89,54,45.

Explanation:
The numbers from greatest to least is 99,89,54,45.

Use the numbers to fill in the blanks.

Question 26.
The greatest number is __________.
Answer:
100.

Explanation:
The greatest number is 100.

Question 27.
The least number is __________.
Answer:
46.

Explanation:
The least number is 46.

Question 28.
__________, __________, and ________ are less than 84.
Answer:
46,67 and 73.

Explanation:
46,63 and 73 are less than 84.

Question 29.
____________ and __________ are greater than 84.
Answer:
92,100.

Explanation:
92 and 100 are greater than 84.

Question 30.
67 is greater than ___________ but less than 100.
Answer:
46.

Explanation:
67 is greater than 46 but less than 100.

Question 31.
92 is less than ___________ but greater than 84.
Answer:
100.

Explanation:
92 is less than 100 but greater than 84.

Complete each number pattern.

Question 32.
50, 51, 52, __________, 54, 55, __________, __________, 58
Answer:
50,51,52,53,54,55,56,57,58.

Explanation:
The complete pattern is 50,51,52,53,54,55,56,57,58.

Question 33.
73, 72, 71, __________, __________, 68, __________
Answer:
73,72,71,70,69,68,67.

Explanation:
The complete pattern is 73,72,71,70,69,68,67.

Question 34.
__________, 87, 89, __________, 93, __________
Answer:
85,87,89,91,93,95.

Explanation:
The complete pattern is 85,87,89,91,93,95.

Question 35.
99, __________, 95, 93, __________, __________
Answer:

Question 36.
50, 60, __________, 80, __________, __________
Answer:
50,60,70,80,90,100.

Explanation:
The complete pattern is 50,60,70,80,90,100.

Question 37.
93, 83, 73, __________, __________, 43, __________
Answer:
93,83,73,63,53,43,33.

Explanation:
The complete pattern is 93,83,73,63,53,43,33.

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 8 Addition and Subtraction Facts to 20 to score better marks in the exam.

Math in Focus Grade 1 Chapter 8 Answer Key Addition and Subtraction Facts to 20

Put On Your Thinking Cap!

Challenging Practice

Question 1.
10 6 = 4
Answer: 10 – 6 = 4

Question 2.
7 5 = 12
Answer: 7 + 5 = 12

Question 3.
16 9 = 7
Answer: 16 – 9 = 7

Question 4.
9 7 = 16
Answer: 9 + 7 = 16

Question 5.
11 3 = 14
Answer: 11 + 3 = 14

Question 6.
14 6 = 20
Answer: 14 + 6 = 20

Question 7.
17 2 = 15
Answer: 17 – 2 = 15

Question 8.
12 8 = 20
Answer: 12 + 8 = 20

Fill in the blanks.

Question 9.
18 – ______ = 10
Answer: 18 – 8 = 10

Question 10.
______ – 9 = 11
Answer: 20 – 9 = 11

Question 11.
20 – ______ = 20
Answer: 20 – 0 = 20

Question 12.
______ – 6 = 6
Answer: 12 – 6 = 6

Question 13.
______ + 3 = 12
Answer: 9 + 3 = 12

Question 14.
______ + 5 = 13
Answer: 8 + 5 = 13

Solve.

Question 15.
Dane gets 2 baskets in a computer game. His total score is 16.

a. Color 2 baskets that he gets.

Answer:

b. Which are the 2 baskets that he got? Write an addition sentence for them.
_____ + _____ = 16
Answer: 11 + 5 = 16

c. Look for other answers. Write them here.
___ + ___ = 16
___ + ___ = 16
Answer:
12 + 4 = 16
9 + 7 = 16

Put On Your Thinking Cap!

Problem Solving

Solve.

Ed did 6 more cartwheels than Lila. How many cartwheels did Ed and Lila each do?

Write four possible pairs of numbers. The total number of cartwheels cannot be more than 20.

Question 1.
If Lila did ________ cartwheels, then Ed did ________ cartwheels.
Answer: If Lila did 7 cartwheels, then Ed did 13 cartwheels.
7 + 13 = 20

Question 2.
If Lila did ________ cartwheels, then Ed did ________ cartwheels.
Answer: If Lila did 8 cartwheels, then Ed did 12 cartwheels.
8 + 12 = 20

Question 3.
If Ed did ________ cartwheels, then Lila did ________ cartwheels.
Answer: If Ed did 14 cartwheels, then Lila did 6 cartwheels.
14 + 6 = 20

Question 4.
If Ed did ________ cartwheels, then Lila did ________ cartwheels.
Answer:
If Ed did 10 cartwheels, then Lila did 10 cartwheels.
10 + 10 = 20

Fill the with any of these numbers. Use each number once.

Question 5.

Answer:

Chapter Review/Test

Vocabulary

Circle the correct answers.

Question 1.
Which numbers are the same?
4 9 6 0 4
Answer: 4 and 4 are the same numbers

Question 2.
Which fact is a doubles fact?
9 + 1 = 10 4 + 8 = 12 9 + 9 = 18
Answer: 9 + 9 = 18 is a doubles fact.

Question 3.
Which fact is a doubles plus one fact?
1 + 2 = 3 3 + 3 = 6 9 + 2 = 11
Answer: 1 + 2 = 3 is a doubles plus one fact.

Concepts and Skills
Fill in the blanks.

Question 4.
6 + 5 = ____
Answer: 11

Question 5.
9 + 6 = ___
Answer: 15

Complete the number bonds. Then fill in the blanks.

Question 6.

Answer:

Question 7.

Answer:

Question 8.

Answer:

Question 9.

Answer:

Fill in the blanks.

Question 10.
11 + 9 = ____
Answer: 20

Question 11.
12 – 5 = ____
Answer: 7

Problem Solving

Solve.

Question 12.
Andy has 9 stickers. His sister gives him 5 more. How many stickers does Andy have in all?

Andy has ________ stickers in all.
Answer:
Given,
Andy has 9 stickers,
His sister gave 5 more stickers,
By adding 9 with 5 we get 14,
Therefore, Andy has 14 stickers in all.

Question 13.
Tia has 14 hair clips. She gives 7 hair clips to her sister. How many hair clips does Tia have left?
Tia has ________ hair clips left.

Answer:
Given,
Tia has 14 hair clips,
She gives away 7 hair clips to her sister,
By subtracting 7 from 14 we get 7,
Therefore, Tia has 7 hair clips left.

Question 14.
I am double 6 plus 1 more. What number am I? I am the number ____
Answer:
I am the number 13.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 14 Practice 1 Prisms and Pyramids provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 14 Practice 1 Answer Key Prisms and Pyramids

Identify the type of pyramid and the shapes of the faces

Question 1.
This is a ___ prism.
Answer:
This is a triangular prism,

Explanation:
A triangular prism is a prism composed of two triangular bases and
three rectangular sides.

Question 2.
Two of its faces are ____
Answer:
Two of its faces are triangle,

Explanation:
A triangular prism is a prism composed of two triangular bases.

Question 3.
Three of its faces are ____
Answer:
A triangular prism is a prism composed of three rectangular sides.

Question 4.
This is a ____ prism.
Answer:
This is a rectangular prism,

Explanation:
As a rectangular prism is a three-dimensional shape, having six faces,
where all the faces (top, bottom, and lateral faces) are rectangle of the prism.
So given solid is rectangular prism.

Question 5.
All its faces are _______________________
Answer:
All its faces are rectangle,

Explanation:
As a rectangular prism is a three-dimensional shape, having six faces,
where all the faces (top, bottom, and lateral faces) are rectangle of the prism.

Complete the table.

Question 6.

Answer:

Explanation:
Given type of prism is triangular as the prism is composed of two triangular bases and
three rectangular sides with number of faces – 5, number of edges – 9 & number of vertices – 6.

Question 7.

Answer:

Explanation:
Given type of prism is triangular as the prism is composed of two triangular bases and
three rectangular sides with number of faces – 5, number of edges – 9 & number of vertices – 6.

Question 8.

Answer:

Explanation:
Given a pentagonal prism is a three-dimensional solid that has two
pentagonal bases on the bottom and top of the shape.
All the other sides of a pentagonal prism have the shape of a rectangle.
There are types of pentagonal prism – regular pentagonal prism and
rectangular pentagonal prism.
A pentagonal prism has 7 faces, 15 edges and 10 vertices.

Identify the type of pyramid and the shape of the faces.

Question 9.
This is a ___ pyramid.
Answer:

Explanation:
Given pyramid is Tetragonal or Dipyramid with 4 prisms.

Question 10.
All its faces are __.
Answer:

All its faces are 8,

Explanation:
Given Tetragonal or Dipyramid has 8-faced form about a 4-fold rotation axis.

Identify the type of pyramid and the shapes of the faces.

Question 11.
This is a ___ pyramid.
Answer:

Answer:
This is a _tetragonal- dipyramid__ pyramid.

Explanation:
Given pyramid is Tetragonal or Dipyramid with 4 prisms.

Question 12.
One of its faces is a ____
Answer:

One of its faces is a rectangular base,

Explanation:
Given pyramid has base of a rectangle as shown above.

Question 13.
Four of its faces are ____
Answer:
Four of its faces are triangular prisms,

Explanation:
As given pyramid has four of its faces are triangular prisms.

Complete the table.

Question 14.

Answer:

Explanation:
Given type of pyramid is pentagonal pyramid number of faces 6, number of edges 10 and
number of vertices 6.

Question 15.

Answer:

Explanation:
Given the type of pyramid is a pentagonal pyramid number of faces 7,
a number of edges 12 and number of vertices 7.

Name the solid formed by each net.

Question 16.

Answer:

Explanation:
Given net is Cube as as it has 6 square faces as shown above.

Question 17.

Answer:

Explanation:
Given net is tetragonal prism as as it has 4 triangular faces and one square face as shown above.

Question 18.

Answer:

Explanation:
Given net is triangular pyramid as as it has 4 triangular faces as shown above.

Question 19.

Answer:

Explanation:
Given prism is rectangular as it has 2 tiangular faces and
3 rectangular faces as shown above.

Question 20.

Answer:

Explanation:
Given net is Cuboid as it has 6 rectangular faces as shown above.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 14 Three-Dimensional Shapes provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 14 Answer Key Three-Dimensional Shapes

Put On Your Thinking Cap!

Challenging Practice

Find the number of cubes in each prism.

Question 1.

Answer:

Explanation:
Given solid cube has 3 cms X 2 cms X 2 cms each.
So the volume of given cube is  (3 cms X 2 cms X 2 cms)  =
12 cubes with 1 cm X 1 cm X 1 cm each.

Question 2.

Answer:

Explanation:
Given cube is divided in center so we get 2 triangular prisms.

Each solid is cut vertically along the line shown. Identify the solid shapes that result.

Question 3.

Answer:

Explanation:
Given solid shape has 3 triangular prisms again 3 have been divided from center
giving 6 solid shape prisms.
Question 4.

Answer:

Explanation:
Given solid shape has 3 irregular triangular prisms again 3 prisms have been
divided from center giving 6 solid shape small prisms.

Put On Your Thinking Cap!

Problem Solving

Which of these are nets of a cube? Check the boxes.

Question 1.

Answer:

Explanation:
Given nets form a cube so checked and ticked in the checkbox.

Question 2.

Answer:

Explanation:
Given nets form a cube so checked and ticked in the checkbox.

Question 3.

Answer:

Explanation:
Given nets form a cube so checked and ticked in the checkbox.

Question 4.

Answer:

Explanation:
Given nets form a cube so checked and ticked in the checkbox.

Question 5.

Answer:

Explanation:
Given nets form a cube so checked and ticked in the checkbox.

Question 6.

Answer:

Explanation:
Given nets cannot form a cube so checked and ticked cross in the checkbox.

Question 7.

Answer:

Explanation:
Given nets cannot form a cube so checked and ticked cross in the checkbox.

Question 8.

Answer:

Explanation:
Given nets cannot form a cube so checked and ticked cross in the checkbox.

Practice the problems of Math in Focus Grade 2 Workbook Answer Key Chapter 7 Practice 4 Comparing Lengths in Centimeters to score better marks in the exam.

Math in Focus Grade 2 Chapter 7 Practice 4 Answer Key Comparing Lengths in Centimeters

Look at each drawing. Then fill in the blanks.

Question 1.
Which is longer? Drawing ___

Answer: Drawing A is longer than Drawing B

Question 2.

Drawing ___ is the shortest.
Drawing ___ is the longest.
Explain your answers.
Answer: Drawing B is the shortest.
Drawing C is the longest.

Find each length.

Question 3.

The straw is about ___ centimeters long.
Answer: The straw is about 8 centimeters long.

Question 4.

The wallet is about ____ centimeters long.
Answer: The wallet is about 6 centimeters long.

Question 5.

The key is about __ centimeters long.

Answer: The key is about 2 centimeters long.

Find each length.

Question 6.

The pen is about _________ centimeters long.
Answer: The pen is about 12 centimeters long

These rulers are smaller than in real life.

Question 7.

The bracelet is about _________ centimeters wide.
Answer: The bracelet is about 5 centimeters wide.

Use your answers for Exercises 3 to 6. Fill in the blanks with longer or shorter.

Question 8.
The pen is _________ than the straw.
Answer: The pen is longer than the straw.

Question 9.
The key is _________ than the pen.
Answer: The key is shorter than the pen.

Question 10.
The wallet ¡s _________ than the straw.
Answer: The wallet is shorter than the straw.

Use your answers for Exercises 3 to 7. Fill in the blanks.

Question 11.
The straw is ___ centimeters longer than the key.
Answer:
The straw is 4 centimeters longer than the key
Explanation:
Given,
Straw is 8 cm,
Key is 4 cm,
By subtracting 4 from 8 we get 4,
Therefore, the straw is 4 centimeters longer than the key.

Question 12.
The straw is ___ centimeters shorter than the pen.
Answer: The straw is 4 centimeters shorter than the pen.
Explanation:
Given,
Straw is 8 cm,
Pen is 12 cm,
By subtracting 8 from 12 we get 4,
Therefore, the straw is 4 centimeters shorter than the Pen

Question 13.
The pen is ____ centimeters longer than the key.
Answer: The pen is 10 centimeters longer than the key.
Explanation:
Given,
Pen is 12 cm,
Key is 2 cm,
By subtracting 2 from 12 we get 10,
Therefore, the Pen is 10 centimeters longer than the key

Question 14.
The bracelet is ___ centimeter shorter than the wallet.
Answer: The bracelet is 1 centimeter shorter than the wallet.
Explanation:
Given,
Bracelet is 5 cm,
Wallet is 6 cm,
By subtracting 5 from 6 we get 1,
Therefore, the bracelet is 1 centimeter shorter than the wallet

Question 15.
The longest object is the _____
Answer: The longest object is the pen with 12 cm long.

Question 16.
The shortest object is the ____
Answer: The shortest object is the key with 2 cm.

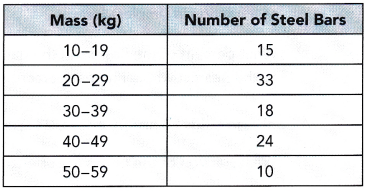
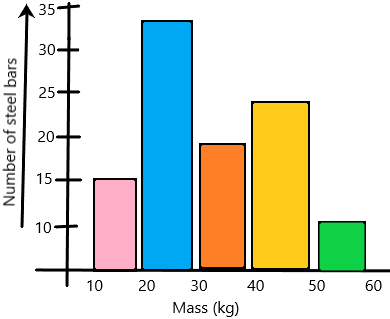
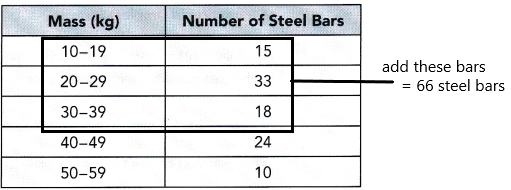
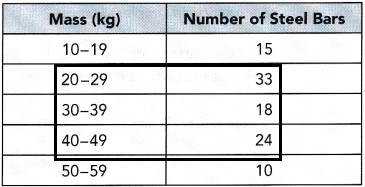
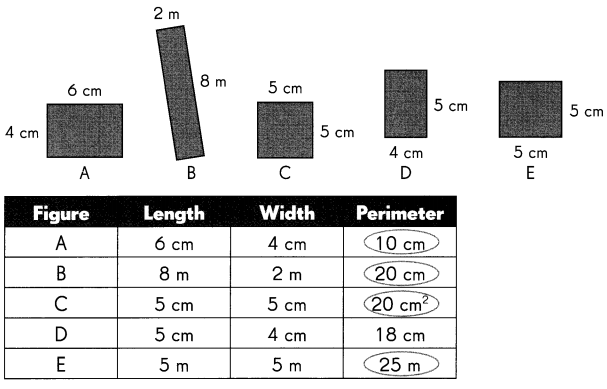
Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 9 Practice 2 Multiplying by Tens, Hundreds, and Thousands to score better marks in the exam.

Math in Focus Grade 5 Chapter 9 Practice 2 Answer Key Multiplying by Tens, Hundreds, and Thousands

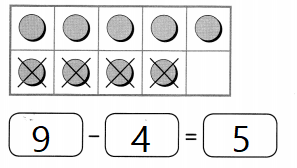
Complete. Draw chips and use arrows to show how the chips move. Then fill in the blanks.

Question 1.

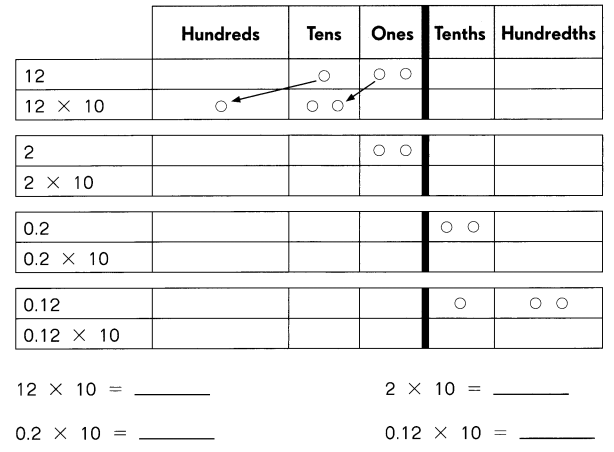
Answer:
12 x 10 = 120
2 x 10 = 20
0.2 x 10 = 2
0.12 x 10 = 1.2
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Multiply.
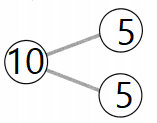
Question 2.

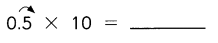
Answer: 5

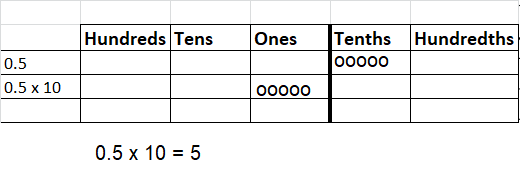
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

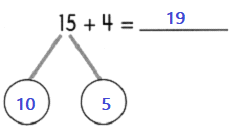
Question 3.

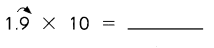
Answer: 19

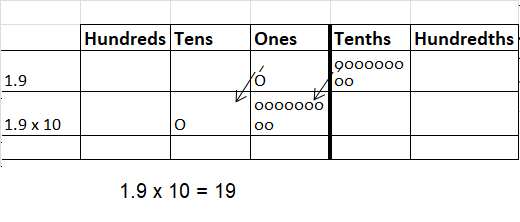
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 4.

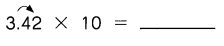
Answer: 34.2

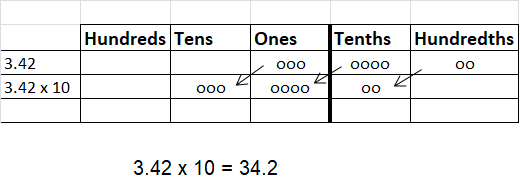
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 5.

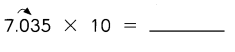
Answer: 70.35

Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 6.
10 × 7.9 = ___
Answer:79

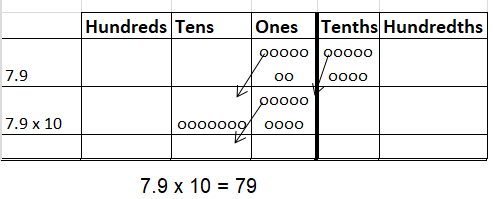
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 7.
10 × 4.8 = ___
Answer: 48

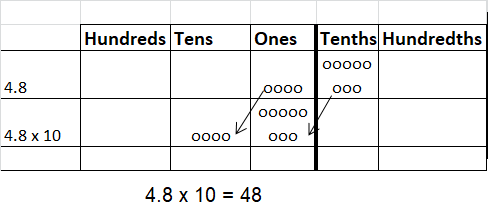
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 8.
10 × 27.54 = ___
Answer: 275.4

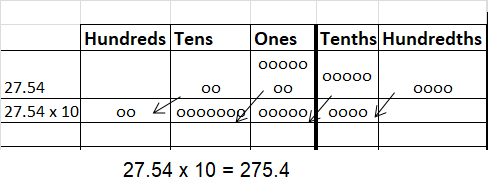
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 9.
10 × 12.009 = ____
Answer: 120.09

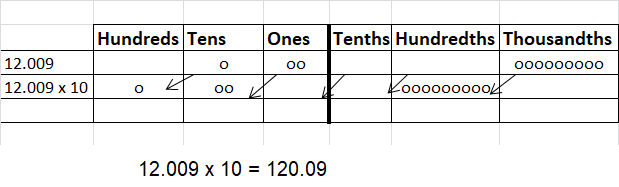
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 10.
0.7 × ___ = 7
Answer: 10
0.7 x 10 = 7

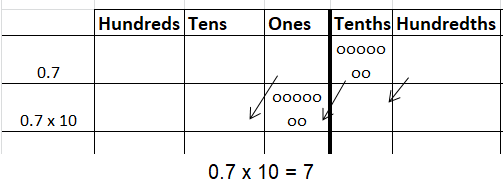
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

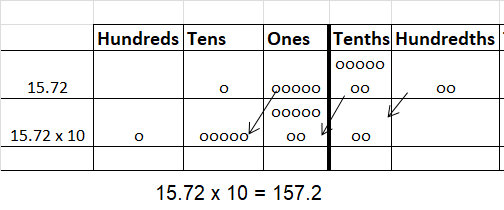
Question 11.
15.72 × ___ = 157.2
Answer: 10
15.72 x 10 = 157.2

Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

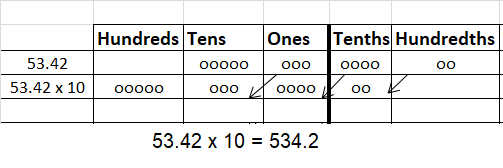
Question 12.
10 × ___ = 534.2
Answer: 534.2

10 x 53.42

Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

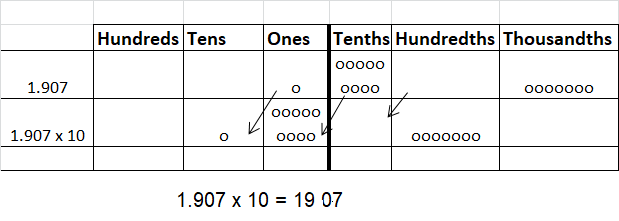
Question 13.
___ × 10 = 19.07
Answer: 1.907
1.907 x 10 = 190.7

Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Complete

Example
8 × 50 = (8 × 5) × 10
= 40 × 10
= 400
So, 8 × 50 = 400

Question 14.
0.8 × 50 = (0.8 × 5) × ___
= ___ × 10
= ____
So, 0.8 × 50 = ___
Answer:
0.8 × 50 = (0.8 × 5) × 10
= 4.0 × 10
= 40
So, 0.8 × 50 = 40
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 15.
0.88 × 50 = (0.88 × ___) × 10
= ___ × 10
= ____
So, 0.88 × 50 = ___
Answer:
0.88 × 50 = (0.88 × 5) × 10
= 4.4 × 10
= 44
So, 0.88 × 50 = 44
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Find each product.

Question 16.
0.9 × 40 = ____
Answer:
0.9 × 40 = (0.9 × 4) × 10
= 3.6 × 10
= 36
So, 0.9 × 40 = 36
Explanation:
Separate 40 as 4 ones and 1 tenths,
then multiply with ones first and later tens.

Question 17.
1.5 × 60 = ___
Answer:
1.5 × 60 = (1.5 × 6) × 10
= 9.0 × 10
= 90
So, 1.5 × 60 = 90

Explanation:
Separate 60 as 6 ones and 1 tenths,
then multiply with ones first and later tens.

Question 18.
0.05 × 80 = ____
Answer:
0.05 × 80 = (0.05 × 8) × 10
= 0.4 × 10
= 4
So, 0.05 × 80 = 4
Explanation:
Separate 80 as 8 ones and 1 tenths,
then multiply with ones first and later tens.

Question 19.
9.17 × 70 = ___
Answer:
9.17 x 70 = (9.17 x 7) x 10
=64.19 x 10
=641.9
So, 9.17 x 70 = 641.9
Explanation:
Separate 70 as 7 ones and 1 tenths,
then multiply with ones first and later tens.

Question 20.
6.358 × 30 = ___
Answer:
6.358 x 30 = (6.358 x 3) x 10
=19.074 x 10
=190.74
So,6.358x 30 = 190.74
Explanation:
Separate 30 as 3 ones and 1 tenths,
then multiply with ones first and later tens.

Question 21.
34.6 × 50 = ____
Answer:
34.6 x 50 = (34.6 x 5) x 10
= 173 x 10
= 1730
So, 34.6 x 50 =1730
Explanation:
Separate 50 as 5 ones and 1 tenths,
then multiply with ones first and later tens.

Question 22.
41.32 × 60 = ___
Answer:
41.32 x 60 = (41.32 x 6) x 10
= 247.92 x 10
= 2479.2
So, 41.32 x 60= 2479.2
Explanation:
Separate 60 as 6 ones and 1 tenths,
then multiply with ones first and later tens.

Question 23.
23.05 × 40 = ___
Answer:
23.05 x 40 = (23.05 x 4) x 10
=92.2 x 10
=922
So, 23.05 x 40 = 92.2
Explanation:
Separate 40 as 4 ones and 1 tenths,
then multiply with ones first and later tens.

Question 24.

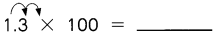
Answer: 130
Explanation:
1.3 x 100 = (1.3 x10) x 10
=13 x 10
=130
So, 1.3 x 100 = 130
Question 25.

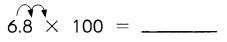
Answer: 680
Explanation:
6.8 x 100 = (6.8 x 10) x 10
= 68 x 10
= 680
So, 6.8 x 100 = 680

Question 26.

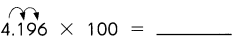
Answer: 419.6
Explanation:
4.196 x 100 = (4.196 x 10) x 10
= 41.96 x 10
= 419.6
So, 4.196 x 100 = 419.6

Question 27.

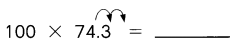
Answer: 7430
Explanation:
74.3 x 100 = (74.3 x 10) x 10
= 743 x 10
= 7430
So, 74.3 x 100 = 7430

Question 28.
46.8 × 1oo = ______
Answer: 4680
Explanation:
46.8 x 100 = (46.8 x 10) x 10
=468 x 10
= 4680

Question 29.
4.68 × 100 = ___
Answer: 468
Explanation:
4.68 x 100 = (4.68 x 10) x 10
=46.8 x 10
= 468
So, 4.68 x 100 = 468

Question 30.
5.095 × 100 = ______
Answer: 509.5
Explanation:
5.095 x 100 = (5.095 x 10 )x 10
= 50.95 x 10
= 509.5
So, 5.095 x 100 = 509.5

Question 31.
100 × 50.95 = ____
Answer: 5095
Explanation:
50.95 x 100 = (50.95 x 10) x 10
= 509.5 x 10
= 5095
So, 50.95 x 100 = 5095

Multiply.

Question 32.

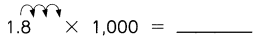
Answer: 1800
Explanation:
1.8 x 1000 = (1.8 x 10) x 10 x 10
= 18 x 10 x 10
=180 x 10
=1800
So, 1.8 x 1000 = 1800
Question 33.

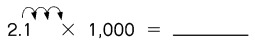
Answer: 2100
Explanation:
2.1 x 1000 = (2.1 x 10) x 10 x 10
=21 x 10 x 10
= 210 x 10
= 2100
So, 2.1 x 1000 = 2100

Question 34.

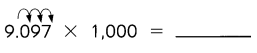
Answer: 9097
Explanation:
9.097 x 1000 = (9.097 x 10) x 10 x 10
=90.97 x 10 x 10
= 909.7 x 10
=9097
So, 9.097 x 1000 = 9097

Question 35.

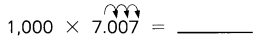
Answer: 7007
Explanation:
7.007 x 1000 = (7.007 x 10) x 10 x 10
= 70.07 x 10 x 10
= 700.7 x 10
= 7007
So, 7.007 x 1000 = 7007

Question 36.
2.74 × 1,000 = ______
Answer: 2740
Explanation:
2.74 x 1000=  (2.74  x 10) x 10 x 10
=27.4 x 10 x 10
=274 x 10
= 2740

Question 37.
27.4 × 1,000 = ____
Answer: 27400
Explanation:
27.4 x 1000 = (27.4 x 10) x 10 x 10
=274 x 10 x10
=2740 x 10
27400

Question 38.
1,000 × 10.81 = ______
Answer: 10810
Explanation:
10.81 x 1000 =(10.81 x 10) x 10 x 10
= 108.1 x10 x 10
= 1081 x 10
= 10810
So, 10.81 x 1000 = 10810

Question 39.
108.1 × 1,000 = ____
Answer: 108100
Explanation:
108.1 x1000 =(108.1 x 10) x 10 x 10
= 1081 x 10 x 10
= 10810 x 10
= 108100
So, 108.1 x 1000 = 108100

Complete.

Example
1.2 = 0.12 × 10
= 0.012 × 100

Question 40.
360 = 36 × ____
= 3.6 × ____
= 0.36 × _____
Answer:
360 = 36 × 10
= 3.6 × 100
= 0.36 × 1000
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 41.
438 = __ × 10
= ___ × 100
= ___ × 1,000
Answer:
438 = 43.8 × 10
= 4.38 × 100
=0.438 × 1,000
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Question 42.
7,256 = ______ × 10
= ____ × 100
= ____ × 1,000
Answer:
7,256 = 725.6 × 10
= 72.56 × 100
= 7.256 × 1,000
Explanation:
To multiply decimals, first multiply as if there is no decimal.
Next, count the number of digits after the decimal in each factor.
Finally, put the same number of digits behind the decimal in the product.

Multiply.

Example
0.3 × 700 = (0.3 × 7) × 1oo
= 2.1 × 1oo = 210
So, 0.3 × 700 = 210

Question 43.
0.003 × 700 = (0.003 × __) × 100
= ____ × 1oo = ____
So, 0.003 × 700 = ___.
Answer:
0.003 × 700 = (0.003 × 7) × 100
= 0.021 × 1oo = 2.1
So, 0.003 × 700 = 2.1.
Explanation:
The place value of a number is the value represented by a digit in a number based on its position in the number.
While a place value is the value a digit holds to be at the place in the number, on the other hand.
First separate the hundredth place value,
and multiply the given numbers with the number .

Question 44.
0.03 × 2,000 = (0.03 × __) × 1,000
= ______ × 1,000 = ______
So, 0.03 × 2,000 = ____.
Answer:
0.03 × 2,000 = (0.03 × 2) × 1,000
= 0.06 × 1,000 = 60
So, 0.03 × 2,000 = 60.
Explanation:
The place value of a number is the value represented by a digit in a number based on its position in the number.
While a place value is the value a digit holds to be at the place in the number, on the other hand.
First separate the place value,
and multiply the given numbers with the number .

Question 45.
0.003 × 2,000 = (0.003 × __________) × 1,000
= __________× 1,000 = _______.
So, 0.003 × 2000 = __________.
Answer:
0.003 × 2,000 = (0.003 × 2) × 1,000
= 0.006× 1,000 = 6
So, 0.003 × 2000 = 6.
Explanation:
The place value of a number is the value represented by a digit in a number based on its position in the number.
While a place value is the value a digit holds to be at the place in the number, on the other hand.
First separate the place value,
and multiply the given numbers with the number .

Find each product.

Question 46.
4.5 × 200 = _______
Answer: 900
Explanation:
(4.5 x 2) x 10 x 10
= 9 x 10 x 10
= 90 x 10
= 900
So, 4.5 x 200 = 900

Question 47.
0.49 × 300 = ___
Answer: 147
Explanation:
0.49 x 300 = (0.49 x 3) x 10 x 10
= 1.47 x 10 x 10
= 14.7 x 10
= 147
So, 0.49 x  300 = 147

Question 48.
3.148 × 500 = ______
Answer: 1,574
Explanation:
3.148 x 500 = (3.148 x 5) x 10 x 10
= 15.74 x 10 x 10
= 157.4 x 10
= 1574
So, 3.147 x 500 = 1574

Question 49.
2.27 × 700 = ___
Answer: 1,589
Explanation:
2.27 x 700 = (2.27 x 7) x 10 x 10
= 15.89 x10 x10
= 158.9 x 10
= 1589
So , 2.27 x 700 = 1589

Question 50.
900 × 3.18 ______
Answer: 2,862
Explanation:
3.18 x 900 = (3.18 x 9) x 10 x 10
= 28.62 x 10 x 10
= 286.2 x 10
= 2862
So, 3.18 x 900 = 2862

Question 51.
1.8 × 2,000 = ___
Answer: 36,00
Explanation:
1.8 x 2000 = (1.8 x 20) x 10 x 10
= 36 x 10 x 10
=360 x 10
=3600
So, 1.8 x 2000 = 3600

Question 52.
4,000 × 2.5 = _______
Answer: 10,000
Explanation:
2.5 x 4000 = (2.5 x 40) x 10 x 10
= 100 x10 x10
= 1000 x 10
= 10000
So, 2.5 x 4000 = 10000

Question 53.
72.5 × 6,000 = ___
Answer: 435,000
Explanation:
72.5 x 6000 = ( 72.5 x 60) x 10 x 10
= 4350 x10 x10
= 43500 x 10
= 435000
So, 72.5 x 6000 = 435000

Question 54.
1.75 × 8,000 = ______
Answer: 14,000
Explanation:
1.75 x 8000 = (1.75 x 80) x 10 x 10
= 140 x10 x10
= 1400 x10
= 14000
So 1.75 x 8000 = 14000

Question 55.
4.19 × 9,000 = ___
Answer: 37,710
Explanation:
4.19 x 9000 = (4.19 x90) x 10 x 10
= 377.1 x10 x10
= 3771 x 10
= 37710
So, 4.19 x 9000 = 37710

శివ అష్టోత్తర శతనామావళిః

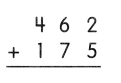
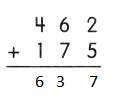
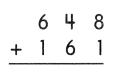
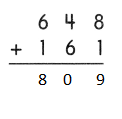
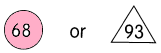
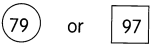
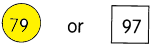
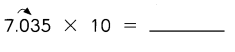
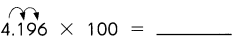
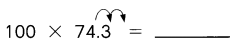
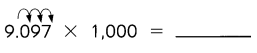
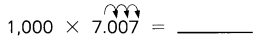
This handy Math in Focus Grade 7 Workbook Answer Key Chapter 10 Probability detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 10 Answer Key Probability

Math in Focus Grade 7 Chapter 10 Quick Check Answer Key

Solve.

Question 1.
Express 10 ounces out of 25 ounces of baking flour as a fraction in the simplest form.
Answer:
Explanation:
In mathematics, a fraction is a number that represents a part of a whole. It consists of a numerator and a denominator. The numerator represents the number of equal parts of a whole, while the denominator is the total number of parts that make up said whole.

This can be written as 10/25
– In the fraction 10/25, the numerator is 10 and the denominator is 25.
– A more illustrative example could involve a box with 25 ounces of baking flour. 1 of those 10 ounces would constitute the numerator of a fraction, while the total of 25 ounces that comprises the whole box would be the denominator.
– Note that the denominator of a fraction cannot be 0, as it would make the fraction undefined.

Question 2.
12 out of 40 pieces of fruit in a basket are lemons. What fraction of the pieces of fruit are lemons? Write your answer in the simplest form.
Answer: 12/40
Explanation:
The total number of fruits in a basket=40
The number of lemons is there=12
We need to write the fraction of the pieces of fruit are lemons=X

– In the fraction 12/40, the numerator is 12 and the denominator is 40.
– A more illustrative example could involve a box with 40 pieces of fruits. 12 of those are lemons would constitute the numerator of a fraction, while the total of 40 pieces of fruits that comprises the whole box would be the denominator.
– Note that the denominator of a fraction cannot be 0, as it would make the fraction undefined.
X=12/40

Question 3.
If there are 36 boys in a group of 50 students, what percent of the students are girls?
Answer:28% are girls.
Explanation:

The total number of students=50
Number of boys $=36$$\therefore$ Number of girls =50−36=14
∴ Percentage of girls =14/50​×100=28%

Write each fraction as a percent. Round your answer to 2 decimal places when you can.

Question 4.
\(\frac{5}{8}\)
Answer: 62.5%
This can be written in a fraction like 5/8.
When it converted into percentage then it becomes 62.5%.
Calculation:
= (5/8) × 100%
= 62.5%
Therefore, 62.5 rounded to 2 decimal places is 62.50.

Question 5.
\(\frac{2}{5}\)
Answer: 40%
This can be written in a fraction like 2/5.
When it is converted into percentage then it becomes 40%.
Calculation:
= (2/5) × 100%
= 40%
Therefore, 40 rounded to 2 decimal places is 40.00.

Question 6.
\(\frac{24}{9}\)
Answer: 266.66666667%
Explanation:
This can be written in a fraction like 24/9.
When it is converted into a percentage then it becomes 266.66666667%
Calculation:
= (24/9) × 100%
= 266.66666667%
Therefore, 266.6666 rounded to 2 decimal places is 266.67

Write each percent as a fraction or a mixed number in simplest form.

Question 7.
54%
Answer: 27/50
Explanation:
To convert percentages to fractions:
Step 1: Write down the percent divided by 100 like this: percent/100.
Step 2: If the percent is not a whole number, then multiply both top and bottom by 10 for every number after the decimal point. (For example, if there is one number after the decimal, then use 10, if there are two then use 100, etc.)
Therefore, 54/100=0.54
This can be simplified as:

The mixed number can be written as:
since 27/50 is a proper fraction, it cannot be written as a mixed number.
If the numerator is greater than or equal to the denominator of a fraction, then it is called an improper fraction. In that case, you could convert it into a whole number or mixed number fraction.
Therefore, 27/50 = Proper Fraction.

Question 8.
19.5%
Answer:39/200
To convert percentages to fractions:
Step 1: Write down the percent divided by 100 like this: percent/100.
Step 2: If the percent is not a whole number, then multiply both top and bottom by 10 for every number after the decimal point. (For example, if there is one number after the decimal, then use 10, if there are two then use 100, etc.)
Therefore, 19.5/100=0.195
This can be simplified as:

The mixed number can be written as:
since 39/200 is a proper fraction, it cannot be written as a mixed number.
If the numerator is greater than or equal to the denominator of a fraction, then it is called an improper fraction. In that case, you could convert it into a whole number or mixed number fraction.
Therefore, 39/200 = Proper Fraction.
The fraction is already in mixed form.

Question 9.
1.4%
Answer: 7/500
To convert percentages to fractions:
Step 1: Write down the percent divided by 100 like this: percent/100.
Step 2: If the percent is not a whole number, then multiply both top and bottom by 10 for every number after the decimal point. (For example, if there is one number after the decimal, then use 10, if there are two then use 100, etc.)
Therefore, 1.4/100=0.014
This can be simplified as:

The mixed number can be written as:
since 7/500 is a proper fraction, it cannot be written as a mixed number.
If the numerator is greater than or equal to the denominator of a fraction, then it is called an improper fraction. In that case, you could convert it into a whole number or mixed number fraction.
Therefore, 7/500 = Proper Fraction.
The fraction is already in mixed form.

Question 10.
115%
Answer: 23/20
Explanation:
To convert percentages to fractions:
Step 1: Write down the percent divided by 100 like this: percent/100.
Step 2: If the percent is not a whole number, then multiply both top and bottom by 10 for every number after the decimal point. (For example, if there is one number after the decimal, then use 10, if there are two then use 100, etc.)
Therefore, 115/100=1.15
This can be simplified as:

The mixed number can be written as:
– Convert the fraction to a mixed number by using long division to find the quotient and remainder.
23÷20=1R3
– The quotient will be the whole number in the fraction, and the remainder will be the numerator in the mixed fraction.
23/20=1  3/20

Write each percent as a decimal.

Question 11.
28%
Answer: 0.28
Explanation:
Percent” means “per 100” or “over 100”. To convert 28% to a decimal rewrite 28 percent in terms of per 100 or over 100.
28% = 28 over 100 or,
28%= 28/100
28 over 100 is the same as 28 divided by 100. Completing the division we get:
28 ÷ 100 = 0.28
Therefore, we have shown that:
28% = 0.28
Simplified conversion:
Remove the percent sign % and divide by 100.
28 ÷ 100 = 0.28
Shortcut conversion:
Move the decimal point 2 places to the left and remove the percent sign %
28% becomes 0.28.

Question 12.
9%
Answer: 0.09
Explanation:
“Percent” means “per 100” or “over 100”. To convert 9% to a decimal rewrite 9 percent in terms of per 100 or over 100.
9% = 9 over 100 or,
9%=9/100.
9 over 100 is the same as 9 divided by 100. Completing the division we get:
9 ÷ 100 = 0.09
Therefore, we have shown that
9% = 0.09
Simplified conversion:
Remove the percent sign % and divide by 100.
9 ÷ 100 = 0.09
Shortcut conversion:
Move the decimal point 2 places to the left and remove the percent sign %
9% becomes 0.09

Question 13.
34.5%
Answer: 0.345
Explanation:
“Percent” means “per 100” or “over 100”. To convert 34.5% to a decimal rewrite 34.5 percent in terms of per 100 or over 100.
34.5% = 34.5 over 100 or,
34.5%=34.5/100
34.5 over 100 is the same as 34.5 divided by 100. Completing the division we get:
34.5 ÷ 100 = 0.345
Therefore, we have shown that
34.5% = 0.345
Simplified conversion:
Remove the percent sign % and divide by 100.
34.5 ÷ 100 = 0.345
Shortcut conversion:
Move the decimal point 2 places to the left and remove the percent sign %
34.5% becomes 0.345

Question 14.
256%
Answer: 2.56
Explanation:
“Percent” means “per 100” or “over 100”. To convert 256% to a decimal rewrite 256 percent in terms of per 100 or over 100.
256% = 256 over 100 or,
256%=256/100
256 over 100 is the same as 256 divided by 100. Completing the division we get:
256 ÷ 100 = 2.56
Therefore, we have shown that
256% = 2.56
Simplified conversion:
Remove the percent sign % and divide by 100.
256 ÷ 100 = 2.56
Shortcut conversion:
Move the decimal point 2 places to the left and remove the percent sign %
256% becomes 2.56

Solve.

Question 15.
A flower bed contains marigolds and zinnias. The ratio of marigolds to zinnias is 7 to 11.
a) What fraction of the flowers in the garden are marigolds? Write your answer a? a fraction in simplest form.
Answer:
Explanation:
The total number of flower beds= 7+11=18
The number of marigolds=7
The number of zinnias=11
The ratio of marigolds to zinnias=7:11
In the above-given question, we need to write the fraction of the flowers in the garden are marigolds.
Already we know that the marigolds are 7.
– In fraction 7/18, the numerator is 7 and the denominator is 18.

– A more illustrative example could involve a box with 18. 7 of those are marigolds would constitute the numerator of a fraction, while the total of 18 flower beds that comprises the whole box would be the denominator.
– Note that the denominator of a fraction cannot be 0, as it would make the fraction undefined.

b) What percent of the flowers in the garden are marigolds? Round your answer to the nearest whole number percent.
Answer: 39%
The fraction of flowers in the garden are marigods=7/18   (check in the above question (a))
When it is converted into percentages then it becomes 38.888888889%
Calculation:
(7/18) × 100%
= 38.888888889%
= 0.38888888889
The nearest whole number percentage of 38.888888889% is 39%.
Note:
– When rounding percentages, we rounded up or down to the nearest number of decimals you wanted.
– We rounded up if the next decimal was five or above, and down if it was four or less.

Question 16.
A bookcase holds 20 history books, 23 science fiction books, and 49 mystery books.
a) What fraction of the books are science fiction books?
Answer:
Explanation:
The total number of books a bookcase holds=20+23+49=92
The number of history books=20
The number of science fiction books=23
The number of mystery books=49
In mathematics, a fraction is a number that represents a part of a whole. It consists of a numerator and a denominator. The numerator represents the number of equal parts of a whole, while the denominator is the total number of parts that make up said whole.
This can be written as 23/92
– In the fraction 23/92, the numerator is 23 and the denominator is 92.
.
– A more illustrative example could involve a box with 92 books. 23 of those are science fiction books would constitute the numerator of a fraction, while the total of 92 books that comprises the whole box would be the denominator.
– Note that the denominator of a fraction cannot be 0, as it would make the fraction undefined.

b) What percent of the books are science fiction books?
Answer: 25%
Explanation:
The fraction of science fiction books=23/92   (check in the above question (a))
When it is converted into percentages then it becomes 25%
Calculation:
(23/92) × 100%
= 25%

Solve.

Question 17.
The table shows the mass of 100 steel bars rounded to the nearest kilogram.

a) Draw a histogram to display this information.
Answer:
A histogram is the graphical representation of data where data is grouped into continuous number ranges and each range corresponds to a vertical bar.
– The horizontal axis displays the number range.
– The vertical axis (frequency) represents the amount of data that is present in each range.
– The number ranges depend upon the data that is being used.
Histogram graph:
A histogram graph is a bar graph representation of data. It is a representation of a range of outcomes into columns formation along the x-axis. in the same histogram, the number count or multiple occurrences in the data for each column is represented by the y-axis. It is the easiest manner that can be used to visualize data distributions. Let us understand the histogram graphby plotting one for the given below example.

b) How many steel bars have a mass from 10 to 39 kilograms?
Answer: 66 steel bars.
Explanation:
The number of steel bars of mass from 10-19=15
The number of steel bars of mass from 20-29=33
The number of steel bars of mass from 30-39=18
Add all the number of steel bars=15+33+18
therefore, the number of steel bars of the mass 10-39 kgs=66

c) What percent of the steel bars have a mass of at least 20 kilograms, but less than 50 kilograms?
Answer: 75%
Explanation:

The number of steel bars of the mass 20-29 kgs=33
The number of steel bars of the mass 30-39 kgs=18
The number of steel bars of the mass 40-49 kgs=24
The total number of steel bars have a mass of at least 20 kgs, but less than 50 kgs=75
The total number of steel bars=15+33+18+24+10=100
Now first write the fraction.
Fraction=75/100
When it is converted into percentages then it becomes 75%
Calculation:
(75/100) × 100%
= 75%
= 0.75

పార్వతీవల్లభ నీలకంఠాష్టకమ్

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 19 Area and Perimeter provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 19 Answer Key Area and Perimeter

Math Journal

Look at John’s answers for the perimeter of the squares and rectangles.

John’s mistakes are circled. Explain why his answers are not correct.
Answer:
John added only two sides to find perimeter,
the perimeter formulas for rectangles and  square.
The perimeter of a rectangle is the total distance of its outer boundary.
It is twice the sum of its length and width and it is calculated with the help of the formula:
Perimeter = 2(length + width).
Explanation:
The perimeter of a square is defined as the total length that its boundary covers
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side

Write the correct answers.

Example The unit for the perimeter of Figure B should be meter (m).

Question 1.
Perimeter of Figure A: _____________________
Answer: 20 cm
Explanation:
The perimeter of a rectangle is the total distance of its outer boundary.
It is twice the sum of its length and width and it is calculated with the help of the formula.
Perimeter = 2(length + width).
P=2(6 + 4) = 2 x 10 = 20cm

Question 2.
Perimeter of Figure C: _____________________
Answer: 20 cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
P = 4 x s
= 4 x 5 = 20 cm

Question 3.
Perimeter of Figure E: _____________________
Answer: 20cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers.
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side

Put On Your Thinking Cap!

Challenging Practice

Complete.

Question 1.
Draw different rectangles with an area of 12 square centimeters. Then draw different rectangles with an area of 9 square centimeters. How many rectangles can you draw for each area?

Answer:
2 rectangles can be drawn for area of  area 12 square centimeters and,
1 rectangle can be drawn for area of 9 square centimeters.

Explanation:
The area of rectangle (A) is the product of its length ‘a’ and width or breadth ‘b’.
So, Area of Rectangle = (a × b) square units.
The square is a shape with four equal sides.
The area of a square is defined as the number of square units that make a complete square.
It is calculated by using the formula Area = s × s = s² in square units.
So, area = 9 square centimeters.

Solve.

Question 2.
Karl bends a piece of wire into a square as shown.

Answer: 32cm
Explanation:
The perimeter of a square is defined as the total length that its boundary covers,
The formula to calculate the perimeter of a square is as, mathematically expressed as;
Perimeter of square, (P) = 4 × Side
P = 4 x 8 = 32 cm

Which of these rectangles can he make using the same piece of wire?

Answer:
Rectangle B and C perimeter is 32cm.
Explanation:
Perimeter of rectangle A
Perimeter = 2(length + width).
P=2(8 + 4) = 2 x 12 = 24cm

Perimeter of rectangle B
Perimeter = 2(length + width).
P=2(10 + 6) = 2 x 16 = 32cm

Perimeter of rectangle C
Perimeter = 2(length + width).
P=2(11 + 5) = 2 x 16 = 32cm

Perimeter of rectangle D
Perimeter = 2(length + width).
P=2(9 + 8) = 2 x 17 = 34cm

Question 3.
Ally wants to build an exercise pen for her pet rabbit. She has 36 feet of fencing to build a rectangular enclosure in her yard. She wants to carefully plan the length and width of the pen, measuring in units of whole feet.
Find all the possible ways that Ally could build her pen and have a perimeter of 36 feet. Fill in the table below.

Answer:

Explanation:
Ally wants to build an exercise pen for her pet rabbit.
So, Perimeter = 2(length + width)
Perimeter = 2(1 + 17) = 36 ft
Perimeter = 2(2 + 16) = 36 ft
Perimeter = 2(3 + 15) = 36 ft
Perimeter = 2(4 + 14) = 36 ft
Perimeter = 2(5 + 13) = 36 ft
Perimeter = 2(6 + 12) = 36 ft
Perimeter = 2(7 + 11) = 36 ft
Perimeter = 2(8 + 10) = 36 ft
Perimeter = 2(9 + 9) = 36 ft

Question 4.
What are some of the concerns that Ally needs to think of in planning for the exercise pen?
Answer:
Perimeter and area of exercise pen.
length and width of exercise pen.
Explanation:
The above are some of the concerns that Ally needs to think of in planning for the exercise pen.

Put On Your Thinking Cap!

Problem Solving

Solve. Look at this pattern.

What is the area of each figure?

Answer:

Explanation:
In the above picture each area of the square is measured as 1 square centimeter.
In figure A there is only 1 square box.
In figure B there are 3 square boxes.
In figure C there are 5 square boxes.
If the pattern continues, what will the area of Figure E be? Draw Figure E below.
Answer:

the area of Figure D & E

Explanation:
In the above picture each area of the square is measured as 1 square centimeter.
In figure D there are 7 square units.
In figure E there are 9 square units.

Must Read:

INDIAMART Pivot Point Calculator