Hillary

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 18 Lines and Surfaces detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 18 Answer Key Lines and Surfaces

Math Journal

Draw a happy face using curves only.
Answer:

Explanation:
I used curves to draw a happy face.

Draw a sad face using parts of lines and curves.
Answer:

Explanation:
I used parts of lines and curves to draw a sad face.

Put On Your Thinking Cap!

Challenging practice

The shapes at the bottom of this page can be combined to make a square. Color the pieces yellow. Cut them out and paste them below to make the square.

Answer:

Chapter Review/Test

Vocabulary

Fill in the blanks with words from the box.

Question 1.
A ball has a __________ surface.
It can _________ on the ground.
Answer:
A ball has a curved surface.
It can roll on the ground.

Question 2.
A picture has a __________ surface.
You can ___________ pictures on top of each other.
Answer:
A picture has a flat surface.
You can stack pictures on top of each other.

Concepts and Skills

Circle the correct answer.

Question 3.

These are (parts of lines, curves).
Answer:

Explanation:
All the above shapes are parts of lines.

Question 4.

These are (parts of lines, curves).
Answer:

Explanation:
All the above shapes are curves.

Draw

Question 5.
A figure that has five parts of lines and three curves
Answer:

Explanation:
The figure has five parts of lines and three curves.

Question 6.
A figure that has only parts of lines
Answer:

Explanation:
The above figure has only parts of lines.

Question 7.
An object that has only curved surfaces
Answer:

Explanation:
The above object has only curved surfaces.

Question 8.
An object that has two flat surfaces and one curved surface
Answer:

Explanation:
The above object has 2 flat surfaces and 1 one curved surface.

Problem Solving

Each pattern is made of curves and straight lines. Find the pattern. Then complete the pattern.

Question 9.

Answer:

Explanation:
I drew the shape that complete the pattern
The pattern is made up of curves and straight lines.

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 18 Practice 2 Flat and Curved Surfaces detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 18 Practice 2 Answer Key Flat and Curved Surfaces

Look at the objects. Then fill in the blanks.

Example

An 0range has 0 flat surfaces. 1 curved surface.
Answer:

Question 1.

A can has __________ flat surfaces, _________curved surface.
Answer:
A can has 2 flat surface 1 curved surface.

Question 2.

A plastic cup has __________ flat surface. __________ curved surface.
Answer:
A plastic cup has 1 flat surface. 1 curved surface.

Question 3.

The cereal box has __________ flat surfaces, __________ curved surfaces.
Answer:
The cereal box has 6 flat surfaces, 0 curved surfaces.

Look around your home. Find two objects that have only flat surfaces. Name and draw them.

Question 4.
Answer:

A note book has only flat surfaces.

Question 5.
Answer:

Table has only flat surfaces.

Question 6.
Circle the solids that you can not roll.

Answer:

Explanation:
I drew a circle around the shapes that cannot roll.

Question 7.
Circle the solids that you can roll.

Answer:

Explanation:
I drew a circle around the shapes that can roll.

Question 8.
Circle the solids that you can slide.

Answer:

Explanation:
I drew a circle a circle around the shapes that can slide.

Look around your home. Find two objects that have only curved surfaces. Name and draw them.

Question 9.
Answer:

A ball has only curved surface.

Question 10.
Answer:

An egg has only curved surface.

How many flat and curved surfaces does each object have? Write your answers in the table.

Question 11.

Answer:
Basketball and egg has o flat surfaces.

Question 12.

Answer:
A vase has 1 flat surface.

Question 13.

Answer:
Basketball and egg have 1 curved surface.

Question 14.

Answer:
A piece of paper and a library card has 2 flat surfaces.

Question 15.

Answer:
A tissue box and a cereal box have 6 flat surfaces.

Cut out pictures of objects in newspapers or magazines Paste them here. Count the flat and curved surfaces in each object. Write your answers next to the picture.

Question 16.
Answer:

A lunch box have 6 flat surfaces and 0 curved surfaces.

A cone has 1 flat surface and 1 curved surface.

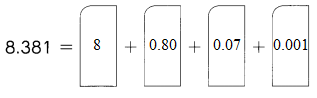
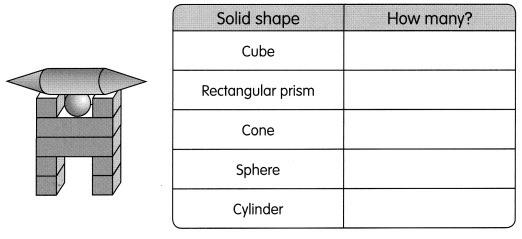
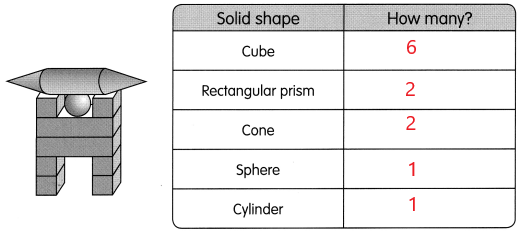
Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 2 Practice 7 Order of Operations to finish your assignments.

Math in Focus Grade 5 Chapter 2 Practice 7 Answer Key Order of Operations

Simplify. Record each step.

Example
18 — 11 — 4 = 3
Step 1: 18 – 11 = 7
Step 2: 7 – 4 = 3
Answer:
3,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 18 – 11 = 7,
Step 2 : 7 – 4 =3.

Question 1.
26 + 8 – 19 = __15__
Step 1 ______
Step 2 ______
Answer:
15,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1 : 26 + 8 = 34,
Step 2 : 34 – 19 = 15.

Question 2.
12 + 16 – 9 + 3 = _22__
Step 1 ___
Step 2 ___
Step 3 ____
Answer:
22,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1:   12 + 16 = 28,
Step 2 : 28 + 3 = 31,
Step 3 :  31 – 9 = 22.

Question 3.
58 – 23 + 11 – 6 = _40__
Step 1 ___
Step 2 ___
Step 3 ____
Answer:
40,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 58 + 11 = 69,
Step 2: 69 – 23 = 46,
Step 3: 46 – 6 = 40.

Simplify. State the order in which you performed the operations.

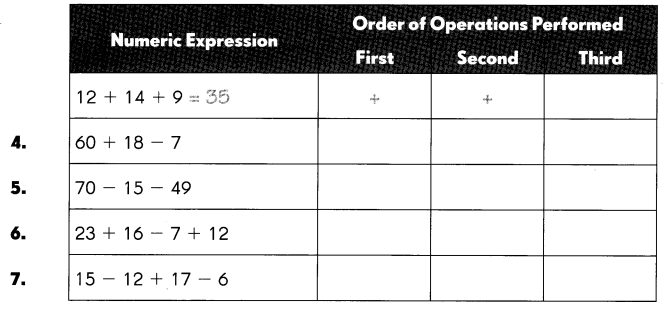
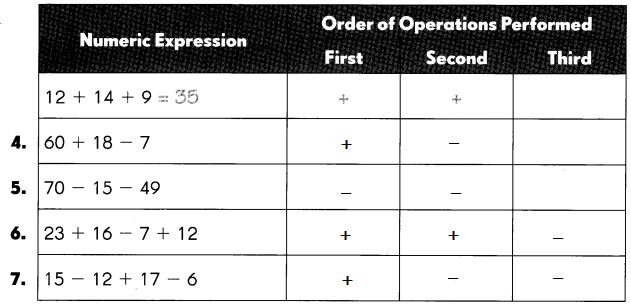
Question 4.
60 + 18 – 7
Answer:
71,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 60 + 18 = 78,
Step 2: 78 – 7 = 71.

Question 5.
70 – 15 – 49 = 6
Answer:
6,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 70 – 49 = 21,
Step 2: 21 – 15 = 6.

Question 6.
23 + 16 – 7 + 12
Answer:
44,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 23 + 16 = 39,
Step 2: 39 + 12 = 51,
Step 3: 51 – 7 = 44.

Question 7.
15 – 12 + 17 – 6
Answer:
14,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 15 + 17 = 32,
Step 2: 32 – 12 = 20,
Step 3: 20 – 6 = 14.

Simplify. Record each step.

Example
9 × 6 ÷ 2 = 27
Step 1: 9 × 6 = 54
Step 2: 54 ÷ 2 = 27

Question 9.
200 ÷ 10 × 3 ÷ 5 = _12__
Step 1 _________
Step 2 _________
Step 3 _________
Answer:
12,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 200 ÷ 10 = 20,
Step 2: 20 ÷ 5 = 4,
Step 3: 4 x 3 = 12.

Question 10.
250 ÷ 5 ÷ 10 × 2 = _10__
Step 1 _________
Step 2 _________
Step 3 _________
Answer:
10,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 250 ÷ 10 = 25,
Step 2: 25 ÷ 5 = 5,
Step 3: 5 x 2 = 10.

Simplify. State the order in which you performed the operations.

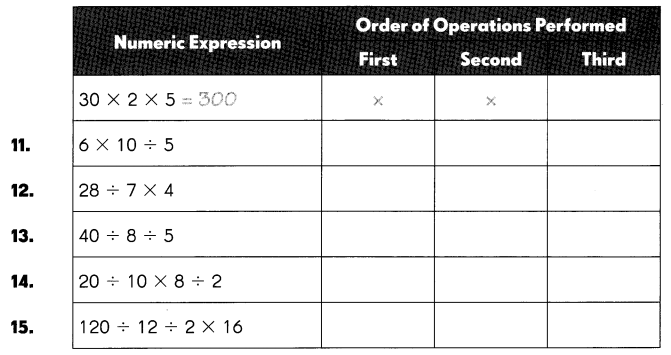
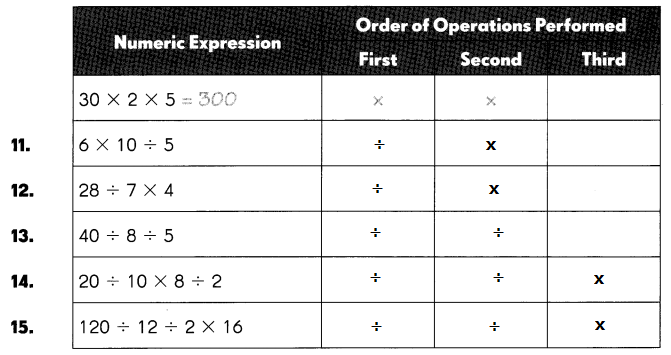
Question 11.
6 × 10 ÷ 5
Answer:
12,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 10 ÷  5 = 2,
Step 2: 6 x 2 = 12.

Question 12.
28 ÷ 7 × 4
Answer:
16,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 28 ÷  7 = 4,
Step 2: 4 x 4 = 16.

Question 13.
40 ÷ 8 ÷ 5
Answer:
1,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 40 ÷  8 = 5,
Step 2: 5 ÷ 5 = 1.

Question 14.
20 ÷ 10 × 8 ÷ 2
Answer:
8,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 20 ÷  10 = 2,
Step 2: 2 ÷  2 = 1,
Step 3: 1 x 8 = 8.

Question 15.
120 ÷ 12 ÷ 2 × 16
Answer:
80,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.

Step 1:
120 ÷  12 = 10,
Step 2:
10 ÷ 2 = 5,
Step 3:
16 x 5 = 80.

Simplify. Record each step.

Example
7 × 8 – 6=50
Step 1: 7 × 8 = 56
Step 2: 56 – 6 = 50

Question 16.
14 + 9 × 7 = __77__
Step 1 ___
Step 2 ____
Answer:
77,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1:  9 x 7 = 63,
Step 2:  63 + 14 = 77.

Question 17.
200 ÷ 20 + 5 = _15__
Step 1 ___
Step 2 ____
Answer:
15,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1 : 200 ÷ 20 = 10,
Step 2 : 10 + 5 = 15.

Question 18.
80 – 16 ÷ 4 = _76__
Step 1 ___
Step 2 ____
Answer:
76,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1:
16 ÷ 4 = 4,
Step 2:  80 – 4 = 76.

Simplify. State the order in which you performed the operations.

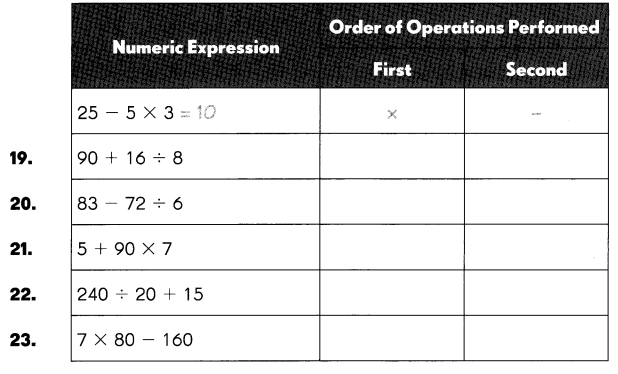
Question 19.
90 + 16 ÷ 8
Answer:
92,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 16 ÷ 8 = 2,
Step 2: 90 + 2 = 92.

Question 20.
83 – 72 ÷ 6
Answer:
71,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 72 ÷ 6 = 12,
Step 2: 83 – 12 = 71.

Question 21.
5 + 90 × 7
Answer:
635,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 90 x 7 = 630,
Step 2: 630 + 5 = 635.

Question 22.
240 ÷ 20 + 15
Answer:
27,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 240 ÷  20 = 12,
Step 2: 12 + 15 = 27.

Question 23.
7 × 80 – 160
Answer:
400,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 80 x 7 = 560,
Step 2: 560 – 160 = 400.

Simplify. Record each step.

Example
54 ÷ 6 + 20 × 4 = 89
Step 1: 54 ÷ 6 = 9
Step 2: 20 × 4 = 80
Step 3: 9 + 80 = 89

Question 24.
40 – 6 + 10 × 3 = _______
Step 1 __________________
Step 2 ________________
Step 3 _____________
Answer:
64,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 10 x 3 = 30,
Step 2: 30 + 40 = 70,
Step 3: 70 – 6 = 64.

Question 25.
36 ÷ 6 – 25 ÷ 5 = _______
Step 1 ________________
Step 2 ________________
Step 3 ___________________
Answer:
1,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 36 ÷  6 = 6,
Step 2: 25 ÷ 5 = 5,
Step 3: 6 – 5 = 1.

Question 26.
25 × 4 – 36 ÷ 9 = ___
Step 1 __________
Step 2 __________
Step 3 ________
Answer:
96,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 36 ÷  9 = 4,
Step 2: 25 x 4 = 100,
Step 3: 100 – 4 = 96.

Simplify. State the order in which you performed the operations.

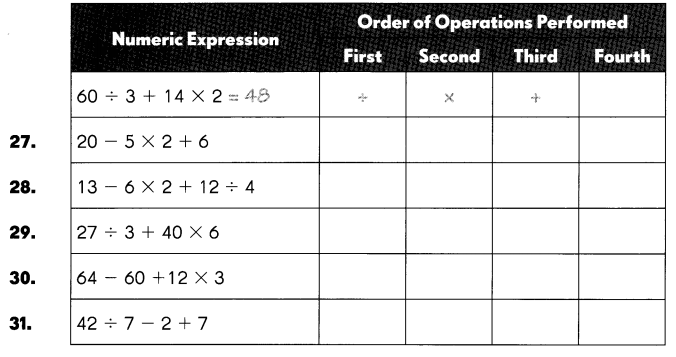
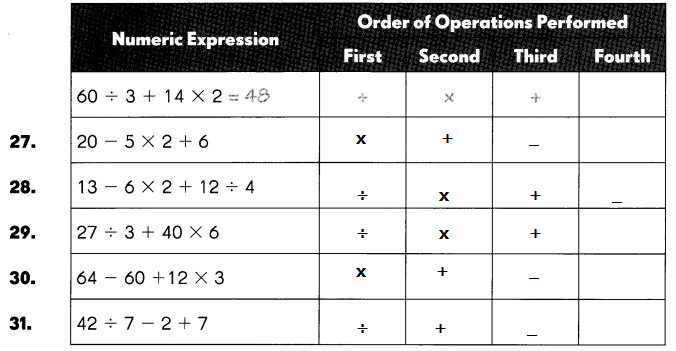
Question 27.
20 – 5 × 2 + 6
Answer:
16,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 5 x 2 = 10,
Step 2: 20 – 10 = 10,
Step 3:  10 + 6 = 16.

Question 28.
13 – 6 × 2 + 12 ÷ 4
Answer:
4,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 12 ÷ 4 = 3,
Step 2: 6 x 2 = 12,
Step 3: 13 – 12 = 1,
Step 4: 3 + 1 = 4.

Question 29.
27 ÷ 3 + 40 × 6
Answer:
249,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 27 ÷ 3 = 9,
Step 2: 40 x 6 = 240,
Step 3: 240 + 9 = 249.

Question 30.
64 – 60 + 12 × 3
Answer:
40,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 12 x 3 = 36,
Step 2: 36 + 64 = 100,
Step 3: 100 – 60 =40.

Question 31.
42 ÷ 7 – 2 + 7
Answer:
11,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 42 ÷ 7 = 6,
Step 2: 6 + 7 = 13,
Step 3: 13  – 2 = 11.

Simplify. Record each step.

Example
(15 – 11) × 9
Step 1: 15 – 11 = 4
Step 2: 4 × 9 = 36

Question 32.
(11 + 5) ÷ 16 = _1__
Step 1 ____
Step 2 ____
Answer:
1,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we use BODMAS rule.
The BODMAS stands for
B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 11 + 5 = 16,
Step 2: 16 ÷ 16 = 1.

Simplify. Record each step.

Question 33.
63 – (9 × 7) = _0_
Step 1 ______
Step 2 ________________
Answer:
0,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
The acronym stands for
B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition and S – Subtraction.
Step 1: 9 x 7 = 63,
Step 2: 63 – 63 = 0.

Question 34.
32 ÷ (14 + 2) = ____
Step 1 __________________
Step 2 __________________
Answer:
2,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
The acronym stands for
B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition and S – Subtraction.
Step 1 : 14 + 2 = 16,
Step 2 : 32 ÷  16 = 2.

Simplify. State the order in which you performed the operations.

Answer:

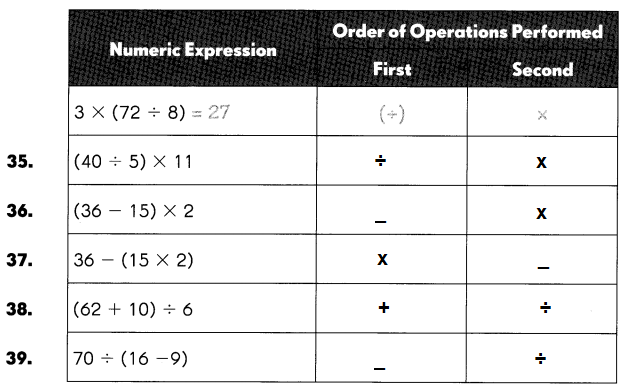
Question 35.

(40 ÷ 5) × 11
Answer:
88,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1 40 ÷  5 = 8,
Step 2 8 x 11 = 88.

Question 36.
(36 – 15) × 2
Answer:
42,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction,
Step 1: 36 – 15 = 21,
Step 2: 21 x 2 = 42.

Question 37.
36 – (15 × 2)
Answer:
6,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for
B – Brackets, O – Order of powers, D – Division, M – Multiplication,
A – Addition, and S – Subtraction.,
Step 1: 15 x 2 = 30,
Step 2: 36 – 30 = 6.

Question 38.
(62 + 10) ÷ 6
Answer:
12,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for
B – Brackets, O – Order of powers, D – Division, M – Multiplication,
A – Addition, and S – Subtraction,
Step 1:
62 + 10 = 72,
Step 2:
72 ÷  6 =12.

Question 39.
70 ÷ (16 – 9)
Answer:
10,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.

Step 1:
16 – 9 = 7,
Step 2 :
70 ÷  7 = 10.

Simplify. Record each step.

Example
21 + (12 + 6) ÷ 3 = 27
Step 1 12 + 6 = 18
Step 2 18 ÷ 3 = 6
Step 3 21 + 6 = 27

Question 40.
7 + (8 – 4) × 10 = _47___
Step 1 _______________
Step 2 _________
Step 3 ______
Answer:
47,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1 : 8 – 4 = 4,
Step 2 : 4 x 10 = 40,
Step 3 : 40 + 7 = 47.

Question 41.
32 ÷ (7 + 1) × 9 – 5 = ____
Step 1 _______________
Step 2 _________
Step 3 ______
Step 4 ______
Answer:
31,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication,
A – Addition, and S – Subtraction.
Step 1  :  7 + 1 = 8
Step 2 : 32  ÷  8 = 4
Step 3 : 4 x 9 = 36
Step 4 : 36 – 5 = 31.

Simplify. Record each step.

Question 42.
(47 + 12) – 10 ÷ 5 × 3 = ___
Step 1 _________________
Step 2 ______________
Step 3 __________________
Step 4 __________________
Answer:
53,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 47 + 12 = 59,
Step 2:  10 ÷ 5 = 2,
Step 3: 2 x 3 =6,
Step 4: 59 – 6 = 53.

Simplify. State the order in which you performed the operations.

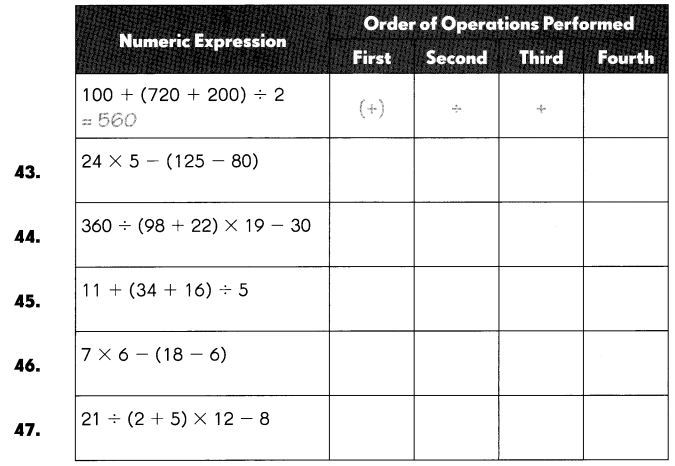
Answer:

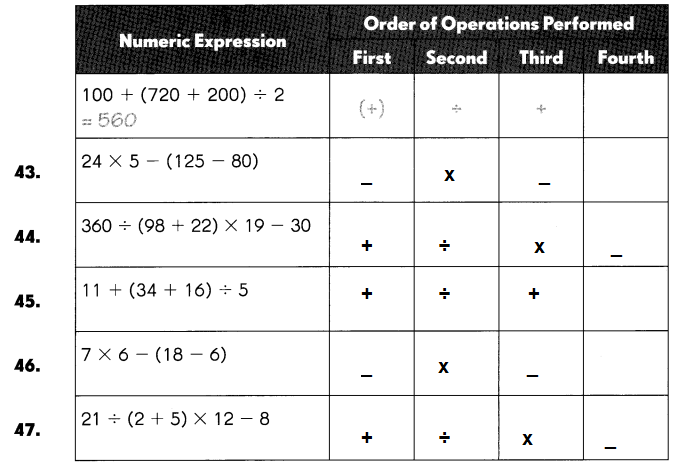
Question 43.
24 × 5 – (125 – 80)
Answer:
75,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers,
D – Division, M – Multiplication, A – Addition, and S – Subtraction.
Step 1 : 125 – 80 = 45,
Step 2 : 24 x 5 = 120,
Step 3: 120 – 45 = 75.

Question 44.
360 ÷ (98 + 22) × 19 – 30
Answer:
27,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers,
D – Division, M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 98 + 22 = 120,
Step 2: 360 ÷ 120 = 3,
Step 3: 3 x 19 = 57,
Step 4: 57 – 30 = 27.

Question 45.
11 + (34 + 16) ÷ 5
Answer:
21,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 34 + 16 = 50,
Step 2: 50 ÷ 5 = 10,
Step 3: 10 + 11 = 21.

Question 46.
7 × 6 – (18 – 6)
Answer:
30,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 18 – 6 = 12,
Step 2: 7 x 6 = 42,
Step 3: 42 – 12 = 30.

Question 47.
21 ÷ (2 + 5) × 12 – 8
Answer:
28,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 2 + 5 = 7,
Step 2: 21 ÷ 7 = 3,
Step 3: 3 x 12 = 36,
Step 4: 36 – 8 = 28.

Simplify. Record each step.

Example
{50 – [13 – (8 + 3)]} ÷ 4 = 12
Step 1 8 + 3
Step 2 13 – 11 = 2
Step 3 50 – 2 = 48</>
Step 4 48 ÷ 4 = 12

Question 48.
19 – [(18 + 2) – 6]
Step 1 __________________
Step 2 __________________
Step 3 __________________
Answer: 5
Step 1 18 + 2 = 20
Step 2 20 – 6 = 14
Step 3 19 – 14 = 5
Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.

Question 49.
[(27 ÷ 9) – 3] + 30 = ___
Step 1 __________________
Step 2 __________________
Step 3 __________________
Answer: 30
Step 1 27 ÷ 9 = 3
Step 2 3 – 3 = 0
Step 3 0 + 30 = 30
Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.

Question 50.
11 + {18 – [15 ÷ (20 – 15)]}= ____
Step 1 __________________
Step 2 __________________
Step 3 __________________
Step 4 __________________
Answer: 26
Step 1 20 – 15 = 5
Step 2 15 ÷ 5 = 3
Step 3 18 – 3 = 15
Step 4 11 + 15 = 26
Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.

Question 51.
{[(100 ÷ 4) × (3 + 3)] ÷ 50} + 9 =
Step 1 ________________
Step 2 _____________
Step 3 __________________
Step 4 __________________
Step 5 __________________
Answer: 12
Step 1 100 ÷ 4 = 25
Step 2 3 + 3 = 6
Step 3 2 5 x 6 = 150
Step 4 150 ÷ 50 = 3
Step 3 + 9 = 12
Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.

Question 52.
(108 – 86) + {120 ÷ [20 – (10 + 6)]} = ___
Step 1 __________________
Step 2 ________________
Step 3 __________________
Step 4 __________________
Step 5 __________________
Answer: 55
Step 1 10 + 6 = 16
Step 2  20 – 16 = 4
Step 3 120 ÷ 4 = 30
Step 4 108 – 86 = 22
Step 5 22 + 30 = 55
Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division, M – Multiplication, A – Addition, and S – Subtraction.

Go through the Math in Focus Grade 5 Workbook Answer Key Mid Year Review to finish your assignments.

Math in Focus Grade 5 Mid-Year Review Answer Key

Test Prep

Multiple Choice
Fill in the circle next to the correct answer.

Question 1.
Which of the following is 3,450,026 in word form? (Lesson 1.1)
(A) Three million, four hundred fifty thousand, twenty-six
(B) Three million, four hundred thousand fifty, twenty-six
(C) Three million, fifty thousand four hundred, twenty-six
(D) Three million, forty-five thousand, twenty-six
Answer:
Option A is the correct answer

Question 2.
Which number is greatest? (Lesson 1.3)
(A) 15,265
(B) 93,216
(C) 320,182
(D) 320,128
Answer:
320182 is the greatest number.
Option C is the correct answer.

Question 3.
Which number when rounded to the nearest thousand is 23,000? (Lesson 1.4)
(A) 22,097
(B) 22,499
(C) 23,400
(D) 23,501
Answer:
22,499 number is rounded to the nearest thousand is 23000.
Option B is the correct answer.

Question 4.
Simplify 20 + 10 × 19 – 7 (Lesson 2.7)
(A) 140
(B) 203
(C) 360
(D) 563
Answer: D
20 + 10 × 19 – 7 = 563
first by adding 20 with 10 we get 30
Now by multiplying 30 with 19 we get 570
From 570 if we remove 7 we get 563
Option D is the correct answer.

Question 5.
Multiply 52 × 10². (Lesson 2.3)
(A) 52
(B) 520
(C) 5,200
(D) 52,000
Answer: C
52 × 10² = 5200
the square of 10 is 100 now by multiplying 100 with 52 we get 5200
Option C is the correct answer.

Question 6.
Which is the difference between the value of the digit 6 in 2,300,628 and in 846,150? (Lesson 1.2)
(A) 600
(B) 5,400
(C) 5,522
(D) 6,000
Answer: B
Digit 6 in 2,300,628 is 600
And digit 6 in 846,150 is 6000
Option B is the correct answer.
Now buy removing 600 from 6000 we get 5400

Question 7.
Which is the remainder when 4,885 is divided by 21? (Lesson 2.6)
(A) 12
(B) 13
(C) 14
(D) 15
Answer:
Remainder is 13.
Option B is the correct answer.

Question 8.
Express 4 ÷ \(\frac{1}{12}\) in simplest form. (Lesson 4.6)
(A) 48
(B) 3
(C) \(\frac{4}{12}\)
(D) \(\frac{1}{48}\)
Answer:
\(\frac{1}{12}\) = 1/12
1/12 ÷ 4 = 3.
Option B is the correct answer.

Question 9.
Find the difference: \(\frac{3}{4}\) – \(\frac{3}{8}\). (Lesson 32)
(A) \(\frac{5}{8}\)
(B) \(\frac{3}{8}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
\(\frac{3}{4}\) = 3/4
\(\frac{3}{8}\) = 3/8
The difference is 3/4 – 3/8 = 3/8.

Question 10.
Find the product: \(\frac{3}{4}\) × \(\frac{8}{12}\)(Lesson 4.1)
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{5}{12}\)
(D) \(\frac{11}{16}\)
Answer:
\(\frac{3}{4}\) = 3/4 \(\frac{8}{12}\) = 8/12
3/4 × 8/12 = 1/2 = \(\frac{1}{2}\)
Option A is the correct answer.

Question 11.
Estimate the sum of \(\frac{6}{7}\) and \(\frac{3}{5}\). (Lesson 3. 1)
(A) 0
(B) \(\frac{1}{2}\)
(C) 1\(\frac{1}{2}\)
(D) 1
Answer:
\(\frac{6}{7}\) = 6/7 \(\frac{3}{5}\) = 3/5
Sum = 6/7 + 3/5 = 1×1/2.
1\(\frac{1}{2}\)
Option C is the correct answer.

Question 12.
What is the difference between 3\(\frac{1}{2}\) and 1\(\frac{1}{4}\) (Lesson 3.6)
(A) 2\(\frac{1}{4}\)
(B) 3\(\frac{1}{4}\)
(C) 4\(\frac{3}{4}\)
(D) 4\(\frac{1}{2}\)
Answer:
3\(\frac{1}{2}\) = 3×1/2 1\(\frac{1}{4}\) = 1×1/4
Difference = 2×1/4 = 2\(\frac{1}{4}\)
Option A is the correct answer.

Question 13.

Find the area of triangle ABC. (Lesson 6.3)

(A) 126 cm²
(B) 98 cm²
(C) 63 cm²
(D) 49 cm
Answer:D
Explanation:
Since area of triangle is A= (Hight × base) /2
Hight = 7 cm
base = 14 cm
so we have (7 × 14)/ 2
7 × 14 =98
98/2=49 cm
Option D is the correct answer.

Question 14.
Simplify 4x + 6 – 2x – 1
(A) 6x + 1
(B) 4x + 3
(C) 8x + 6
(D) 2x + 5
Answer:
Given:
4x + 6 – 2x -1
2x + 5
Option D is the correct answer.

Question 15.
For what value of y will the inequality 3y + 4 < 8 be true? (Lesson 5.4)
(A) y = 1
(B) y = 2
(C) y = 3
(D) y = 4
Answer:
3y + 4 < 8
Take y = 1
3(1) + 4 <8
7<8
Option A is the correct answer.

Question 16.
Glass A contains 236 milliliters of milk. Glass B contains 420 milliliters of milk. What is the ratio of the amount of milk in Glass A to that in Glass B? (Lesson 73)
(A) 89 : 135
(B) 119 : 165
(C) 479 : 660
(D) 59 : 105
Answer:
Glass A contains 236 milliliters of milk
Glass B contains 420 milliliters of milk
236 : 420
= 236/480 = 59/105
= 59 : 105
Option D is the correct answer.

Short Answer

Read the questions carefully. Write your answers in the space provided. Show your work.

Question 17.
What is the missing number in the box? (Lesson 1.2)
87,412 = 80,000 + + 400 + 10 + 2 ____
Answer:
87412 = 80000 + 7000 + 400 + 10 + 2

Question 18.
Order the numbers from greatest to least. (Lesson 1.3)

Answer:
916,236 > 164,239 > 35,982 > 35,928

Question 19.
Find the product of 238 and 4,000. (Lesson 2.2) _____
Answer:
The product of 238 and 4000 = 952000

Question 20.
Simplify 4 × {(43 – 19) + [(121 – 3) ÷ 2]}. (Lesson 2.7)
_____
Answer:
4 × {(43 – 19) + [(121 – 3) ÷ 2]} = 160.

Question 21.
There are 215 Grade 5 students in Cherrywood school. Each student spends $17 on a dictionary. How much in all do the students spend on the dictionary? (Lesson 2.8)
______
Answer:
Total number of students in a grade 5 = 215.
Each student’s spends on a dictionary = 215 × 17 = $ 3655

Question 22.
Mr. Hull is buying computer equipment for his company. The equipment costs $45,900. He pays $5,300 for the first payment. He then pays the rest of the amount in equal payments for 1 4 months. Find the amount he has to pay each month. (Lesson 28)
_________
Answer:
Mr. Hull is buying computer equipment for his company.
The equipment cost = $45900
He pay for the first payment = 5300
He then pay the rest of the amount in equal payments for 14 months.
45900 – 5300 = 40600
40600 ÷ 4 = 2900.

Question 23.
Simplify (2 + 4) × 7 – 6 + 11. (Lesson 2.7)
______
Answer:
(2 + 4) × 7 – 6 + 11
6 × 1 + 11
6 × 12 = 72

Question 24.
Express 38 ÷ 6 as a fraction in simplest from. Then rewrite the fraction as a mixed number. (Lesson 3.3)
_____
Answer:
38 ÷ 6 is in the simplest form = 6.3333

Question 25.
Shaun has 24\(\frac{1}{2}\) ounces of beads. He has 3\(\frac{3}{8}\) ounces of beads less than Tony. Find the weight of Tony’s beads. (Lesson 3.7)
_________
Answer:
Shaun has 24\(\frac{1}{2}\) ounces of beads.
Shaun has 3\(\frac{3}{8}\) ounces of beads less than Tony.
The weight of Tony’s beads = 24\(\frac{1}{2}\) + 3\(\frac{3}{8}\) = 27×\(\frac{7}{8}\)

Question 26.
Express 24\(\frac{1}{4}\) – 15\(\frac{1}{2}\) as a decimal. (Lessons 3.3 and 3.6)
_________
Answer:
24×\(\frac{1}{4}\) – 15×\(\frac{1}{2}\) = 8.75

Question 27.
Lita jogged 7\(\frac{3}{10}\) kilometers on Friday. She jogged 1\(\frac{3}{4}\) kilometers more on Saturday. How many kilometers did she jog on both days? Give your answer as a decimal. (Lesson 3.7)
___________
Answer:
Lita jogged 7×10+3 kilometres on Friday
She jogged 1×4+3 kilometres on Saturday.
She jog on both days = 73 + 7 = 80 kilometres.
80 in decimal = 0.8

Question 28.
Multiply \(\frac{70}{6}\) by \(\frac{18}{4}\). Express the product as a mixed number in simplest form. (Lesson 4.3)
Answer:
\(\frac{70}{6}\) = 70/6 \(\frac{18}{4}\) = 18/4
Product of numbers = 52×1/2

Question 29.
Jamal runs 1\(\frac{3}{10}\) miles a day to train for a race. (Lesson 4.5)

a. If he runs the same distance for 3 days a week, what is the distance he runs in one week?
Answer:
Jamal runs 1×10+3 miles a day to train for a race = 33 miles per a day.
If he runs the same distance for 3 days in a week.
Distance he runs in 1 week = 33 × 3 = 99 miles

b. If he keeps to this training regime for 8 weeks, what is the total distance he will run in 8 weeks?
Answer:
If he keeps to this training regime for 8 weeks.
Total distance he will run in 8 weeks =
1 week = 7 days.
8 weeks = 7×8 = 56
Therefore 33 × 56 = 1848 miles.

Question 30.
A ball of string \(\frac{9}{10}\) meter long is cut into 3 pieces of the same length. Find the length of each piece. (Lesson 4.6)
Answer:
\(\frac{9}{10}\) = 9/10
Ball of string meter long is cut into 3 pieces of the same length = 9/10 ÷ 3 = 3/10.

Question 31.
3 batteries cost $5rand 8 folders cost $2r. Jason bought 6 batteries and 4 folders. How much does he pay? Give your answer in terms of r. (Lesson 5.5)
Answer:
3 batteries cost = $5r
8 folders cost = $2r
Jason bought 6 batteries and 4 folders
6 batteries cost = 3 batteries + 3 batteries = $5r + $5r = $10r.
4 folders cost = $1r
Jason pay = $10r + $1r = $11r.

Question 32.
Find the area. (Lesson 6.1)

Answer:

Question 33.
The base of the triangle ABC is as given. Label its height. (Lesson 6.2)

Answer:

Question 34.
Find the area of triangle PQR. (Lesson 6.3)

Answer: 56cm
Explanation:
Since we know area of triangle 1/2  × BH
B= base = 7 cm
H= Hight = 16cm
so,
1/2 × (7 × 16)
1/2 × (112)
56cm

Question 35.
ABCD and ECFG are rectangles. BC = CF. What is the total area of the shaded parts of the figure? (Lesson 6.3)

Answer: 1750 cm
Explanation:
area of triangle is (BH)/2
for triangle ADE area is
\(\frac{1}{2}\) × (42 × 50) = 1050
for triangle EGF area is
\(\frac{1}{2}\) × (14 × 50) = 350
for triangle BCE area is
\(\frac{1}{2}\) × (14 × 50) = 350
Now by adding all the three we get the total area of the shaded region
that is
1050+350+350=1750 cm

Question 36.
The ratio of the masses of flour in two bags is 5 : 7. The heavier bag contains 1,120 grams of flour. What is the total mass of flour in both bags? (Lesson 7.3)
_________
Answer:
Explanation:
Given:
5 : 7
? : 1,120
Consider x as the other bag content
5 : 7
x : 1,120
by cross multiplication we get
5 × 1120 = 7 × x
5600 = 7x
x=5600/7
x=\(\frac{5600}{7}\)
x=800
therefore the lighter bag contains 800 grams of flour.
Now by adding both we get the total mass of flour in both bags
that is
800 + 1120 = 1920 grams

Question 37.
Rachel, Sally, and Fabio share a pie in the ratio 1 : 2 : 4. What fraction of the pie does Sally get? (Lesson 7.6)
Answer:
Explanation:
Given:
Total shares of pie  present = 1 + 2 + 4 = 7
Rachel’s share = \(\frac{1}{7}\)
Sally = \(\frac{2}{7}\)
Fabio = \(\frac{4}{7}\)
so, fraction of the pie does Sally get is \(\frac{2}{7}\) which is 2/7

Question 38.
The lengths of three sides of a triangle are in the ratio 3 : 4 : 5. The perimeter of the triangle is 156 centimeters. What is the difference in length between the longest and shortest sides? (Lesson 7.6)
___________
Answer:
Explanation:
Given:
lengths of three sides of a triangle are in the ratio 3 : 4 : 5
the perimeter of the triangle is 156 centimeters
Total lengths of three sides of a triangle = 3 + 4 + 5 = 12
Now divide 12 with 156
The quotient will be 13
which means each unit is equal to 13
that is 1 unit =  13
so
for 3 it is = 13 + 13 + 13 = 39
for 4 it is = 13 + 13 + 13 + 13 = 52
for 5 it is = 13 + 13 + 13 + 13 = 65
Now the shortest sides = 39
And the longest side = 65
The difference in length between the longest and shortest sides = 65 – 39 = 26 cm

Question 39.
Look for a pattern in this set of figures. (Lesson 5.1)

a. How many unit squares are in Figure 4? ____
Answer:
16 unit squares are in the figure 4.

b. Which figure in this pattern will have 169 small squares? ____
Answer:
Figure 13 is in the pattern will have 169 small squares.

Extended Response

Solve. Show your work.

Question 40.
Poles are placed an equal distance apart along a 6-kilometer road. There is a tree in between every two poles. The figure shows the distance between a tree and two poles. Poles are placed at the start and end of the road. How many poles are there? (Lesson 2.5)

Answer:
Given that
Poles are placed an equal distance a part along a 6 kilometres on road.
Every tree between two poles.
6 kilometres = 6000 meters
Distance between 2 poles = 400m.
6000/400 = 15.
There are 15 trees together and there are 16 poles together.

Question 41.
A whole number when divided by 4 gives a remainder of 3. The same whole number when divided by 6 gives a remainder of 1. The number is between 70 and 85. What is the number? (Lesson 2.6)
Answer:
The whole number is 79.
79 ÷ 4  the remainder = 3
79 ÷ 6 the remainder = 1

Question 42.
Sarah earns $525 more than Andrew each month. They each spend $1,250 a month and save the rest. Sarah does not have any savings at first. After 11 months, she has $8,250 in savings. How much does Andrew earn in a year? (Lesson 2.8)
Answer:
Explanation:
Given:
Sarah earns $525 more than Andrew each month
They each spend $1,250 a month
After 11 months, she has $8,250 in savings
so, we get
8250 ÷ 11 = 750
Total amount Sarah earns per month is
1250 + 750 = 2000
Total amount Andrew earns per month is
2000 – 525 =1475
So,Andrew earn in a year is
1475 × 12 = 17700 per year

Question 43.
Ivan caught a total of 7\(\frac{2}{5}\) pounds of fish one day. Of the fish caught, 4\(\frac{5}{8}\) pounds were sea bass and the rest were mackerel. He gave away 1\(\frac{7}{8}\) pounds of mackerel. How many pounds of mackerel did he have left? Give your answer as a decimal. (Lesson 3.7)
Answer: \(\frac{36}{40}\) = \(\frac{9}{10}\) = 0.9lbs of mackerel

Question 44.
There were 2\(\frac{4}{5}\) quarts of milk in Container A and some milk in Container B. Lisa poured 1\(\frac{2}{5}\) quarts of milk each into Container A and Container B. In the end, the total volume of milk in the two containers was 10 quarts. How many quarts of milk were in Container B at first? Give your answer as a decimal. (Lesson 3.7)
Answer: 4\(\frac{2}{5}\) = 4\(\frac{4}{10}\) = 4.4 qts

Question 45.
Tyrone read a book for his school project. On the first day, he read 40 pages. On the second day, he read \(\frac{1}{4}\) of the remaining pages. After the second day, he still had to read \(\frac{1}{2}\) of the total number of pages to complete the book. How many pages are in the book? (Lesson 4.2)
Answer:
day one = 40 pages
Total of 6 units
one unit = 20
so for six unit
6 × 20
= 120 pages of book

Question 46.
A dealership has 9y cars, 12y trucks and 18 vans. (Lesson 5.5)

a. 4y cars, 3y trucks and 15 vans are sold. Find the total number of vehicles remaining in terms of y.
Answer:
A dealership has 9y cars, 12y trucks and 18 vans.
He sold 4y cars, 3y cars 15 vans.
Remaining vehicles = 9y – 4y = 5y
12y – 3y = 9y
18 – 15 = 3
Remaining vehicles are 5y cars, 9y trucks and 3 vans.

b. If the value of y is 7, are there more trucks or more cars and vans at first?
Answer:
5y + 9y = 14y
14(7) = 68
There are more trucks at first.

Question 47.
The side of square JKLM is 14 inches. KP = MP = JP = LP. Find the total area of the shaded parts. (Lesson 6.3)

Answer:
Given:
We know the area for triangle is = (BH)/2
For triangle KLQ are is
area =\(\frac{1}{2}\) ×  (14 × 14)
area =\(\frac{1}{2}\) ×  (196)
area =98 in
For triangle KLP are is
area =\(\frac{1}{2}\) ×  (14 × 7)
area =\(\frac{1}{2}\) ×  (98)
area =49 in
The total area of the shaded parts is
98 – 49 = 49 in

Question 48.
Freddie has 2 times as many comic books as David. The ratio of the number of comic books David has to the number of comic books Gary has is 5 : 3. Freddie has 110 comic books. How many comic books do David and Gary have in total? (Lesson 7.6)
Answer: 88 comic books
Explanation:
Given:
Freddie has 2 times as many comic books as David
The ratio of the number of comic books David has to the number of comic books Gary has is
5 : 3
Freddie has 110 comic books which is 2 times David that is 10
so Freddie has 10 units
David has 5 units
And, Gary has 3 units
10 + 5 + 3 = 18 unit
As Freddie has 110 comic books with 10 units
then each unit is = 11
comic books David and Gary have in total is
5 + 3 = 8 × 11 = 88 comic books

Question 49.
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8. Container B contains 900 milliliters of water. (Lesson 7.6)

a. What is the volume of water in Container C?
Answer: 2400 milliliters of water
Explanation:
Given:
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8
A : B : C
2 : 3 : 8
consider B and C container
so we will have
3 : 8
900 : ?
put x in place of the unknown value
we get
3 : 8
900 : x
By cross multiplication we get
3x = 8 × 900
3x = 7200
x = 7200/3
x = \(\frac{7200}{3}\)
x = 2400 milliliters of water
The volume of water in Container C 2400 milliliters of water

b. Find the total volume of water in the three containers.
Answer: 3900 milliliters of water
Explanation:
Given:
The ratio of the volume of water in Container A to the volume of water in Container B to the volume of water in Container C is 2 : 3 : 8
A : B : C
2 : 3 : 8
x : 900 : 2400
consider A and B
2 : 3
x : 900
By cross multiplication we get
3x = 2 × 900
3x = 1800
x= 1800/3
x =  \(\frac{1800}{3}\)
x = 600
now for total volume of water in the three containers add all the three values that is
600 + 900 + 2400 =3900 milliliters of water

Question 50.
Belinda has 10 cups of flour. She uses 3 cups of it to make a loaf of bread. She uses \(\frac{1}{4}\) cup of the remaining flour for each biscuit she wants to make. How many biscuits can she make with the remaining flour?
Answer: 24 biscuit
Given:
Belinda has 10 cups of flour
She uses 3 cups of it to make a loaf of bread.
so , we get
10 – 3 = 7
Now the remaining flour for each biscuit she wants to make.= \(\frac{1}{4}\)
7 × 4
24 biscuit

Questions 51.
Mr. Madison has two boxes of blueberries. At first, Box A had 228 more blueberries than Box B. Mr. Madison transfers 600 blueberries from Box A to Box B. Now Box B contains 5 times as many blueberries as Box A.
How many blueberries were in each box at the beginning?

Answer:
Explatation:
Given:
Box A = 228 more than B
Box B = 5Box A
In box A
243 + 600 = 843
In box B
843 – 288 =615

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 8 Practice 1 Understanding Thousandths to score better marks in the exam.

Math in Focus Grade 5 Chapter 8 Practice 1 Answer Key Understanding Thousandths

Write the decimal shown in the place-value chart.

Example

Question 1.

Answer:

4.055

Question 2.

Answer:

6.009

Write the decimal shown in the place-value chart.

Question 3.

Answer:

5.210

Mark ✗ to show where each decimal is located.

Question 4.
0.006
Answer:

Question 5.
0.024
Answer:

Question 6.
0.033
Answer:

Write the decimal shown by each arrow.

Question 7.

Answer:

Complete.

Question 8.
4 hundredths = ___ thousandths
Answer:
4 hundredths = 40 thousandths

Question 9.
8 tenths 5 hundredths = ____ thousandths
Answer:
8 tenths 5 hundredths = 850 thousandths

Question 10.
20 thousandths = ___ hundredths
Answer:

20 thousandths = 2 hundredths

Question 11.
125 thousandths = 1 tenth ____ thousandths
Answer:
125 thousandths = 1 tenth 25 thousandths

Complete.

Question 12.
0.126 = 1 tenth 2 hundredths ___ thousandths
Answer:
0.126 = 1 tenth 2 hundredths 6 thousandths

Question 13.
0.352 = 3 tenths ____ hundredths 2 thousandths
Answer:
0.352 = 3 tenths 5 hundredths 2 thousandths.

Write the equivalent decimal.

Question 14.
7 thousandths = ___
Answer:
7 thousandths = 0.007

Question 15.
19 thousandths = ____
Answer:
19 thousands = 0.019

Question 16.
235 thousandths = ____
Answer:
235 thousandths = 0.235

Question 17.
300 thousandths = ____
Answer:
300 thousandths = 0.300

Write each fraction as a decimal.

Question 18.
\(\frac{13}{1000}\) = _____
Answer:
The fraction is 13/1000 is in the decision is 0.013.

Question 19.
\(\frac{55}{1000}\) = ____
Answer:
The fraction is 55/1000 is in the decimal is 0.055.

Question 20.
\(\frac{228}{1000}\) = ___
Answer:
The fraction is 228/1000 is in the decimal is 0.228

Question 21.
\(\frac{430}{1000}\) = ___
Answer:
The fraction is 430/1000 is in the decimal is 0.430.

Write each mixed number as a decimal.

Question 22.
2\(\frac{3}{1000}\) = ___
Answer:
2× 3/1000 = 2 × 0.003 = 0.006

Question 23.
6\(\frac{61}{1000}\) = ___
Answer:
6 × 61/1000 = 6 × 0.061 = 0.366

Question 24.
7\(\frac{107}{1000}\) = ___
Answer:
7 × 107/1000 = 7 × 0.107 = 0.749

Question 25.
8\(\frac{240}{1000}\) = ___
Answer:
8 × 240/1000 = 8 × 0.240 = 1.920

Write each improper fraction as a decimal.

Question 26.
\(\frac{1005}{1000}\) = ___
Answer:
The fraction is 1005/1000 = 1.005

Question 27.
\(\frac{1013}{1000}\) = ___
Answer:
The fraction is 1013/1000 = 1.013.

Question 28.
\(\frac{2341}{1000}\) = ___
Answer:
The fraction is 2341/1000 = 2.341.

Question 29.
\(\frac{3450}{1000}\) = ___
Answer:
The fraction is 3450/1000 = 3.450.

Complete.

Question 30.
0.014 _________ thousandths
Answer:
0.014 = 4 thousandths

Question 31.
0.178 = _________ thousandths
Answer:
0.178 = 8 thousandths

Question 32.
0.76 = __________ thousandths
Answer:
0.76 = 6 thousandths

Question 33.
1.035 = 1 one and __________ thousandths
Answer:
1.035 = 1 one and 5 thousandths.

Question 34.

Answer:

4.153can be written in expanded form as 4 + 0.1 + 0.05 + 0.003.

Question 35.

Answer:

8.381 can be written in expanded form as 8 + 0.8 + 0.07 + 0.001

Question 36.
6.426 = ___ + ___ + ___ + _____
Answer:
6.426 can be written in expanded form as 6 + 0.4 + 0.02 + 0.006

Question 37.
3.642 = ___ + ___ + ___ + ____
Answer:
3.642 can be written in expanded form as 3 + 0.6 + 0.04 + 0.002.

Complete.

In 5.074,

Question 38.
the digit 4 is in the ____ place.
Answer:
The digit 4 is in the thousandths place

Question 39.
the value 0f the digit 7 is ____.
Answer:
The value of the digit 7 is in hundredths place

Question 40.
the digit 0 is in the ___ place.
Answer:
The value of 0 is thenth place.

Question 41.
the digit 5 stands for ___.
Answer:
The value of 5 is in one’s place.

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 17 Practice 4 Parallel Lines provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 17 Practice 4 Answer Key Parallel Lines

Guess if the lines are parallel. Count square units between the lines to check your guess.

Question 1.

Answer:
Lines are not parallel
Explanation:

The distance between AX is 1.5 square units and BY is 1 square unit,
distance between the lines AB and XY,
if we extend the lines, they meet at one end, So, the given lines are not parallel lines.

Question 2.

Answer:
lines are parallel lines
Explanation:

LM and PQ are parallel lines and the distance between the lines is more then half square meter,
the lines LM and PQ never meet at any point if we extend.

Question 3.

Answer:
lines are not parallel lines.
Explanation:

The distance between AB is 105 square units and BY is 1 square unit distance between the lines AB and XY
if we extend the lines, they meet at one end.
So, the given lines are not parallel lines.

Question 4.

Answer:
Lines are parallel lines.
Explanation:

KL and MN are parallel lines and the distance between the lines is one square meter,
the lines KL and MN never meet at any point if we extend.
So, the given lines are parallel.

Question 5.

Answer:
Lines are parallel lines.
Explanation:

lm and xy are parallel lines and the distance between the lines is half square meter,
the lines lm and xy never meet at any point if we extend.
So, the given lines are parallel.

Question 6.

Answer:
Lines are not parallel lines

Explanation:
If we extend the lines, they meet at one end,
So, the given lines are not parallel lines.

Check (✓) the box if the lines are parallel.

Answer:

Explanation:
From the above figures we can come to conclusion which figures are parallel lines and which are not parallel lines.

Count square units between lines to find parallel lines. Use a colored pencil to trace a pair of parallel fines in each figure.

Question 7.

Answer:
2 square units

Explanation:
AB and CD are parallel lines and
The distance between AB and CD are 2 square units.

Question 8.

Answer:
4 square units between the parallel lines

Explanation:
pq and rs are parallel lines and
The distance between pq and rs are 4 square units.

Question 9.

Answer:
one square unit between the wx & yz parallel lines

Explanation:
wx and yz are parallel lines and
The distance between wx and yz are 1 square units.

Question 10.

Answer:
2 square units between the parallel lines

Explanation:
wx and yz are parallel lines and
The distance between wx and yz are 2 square units.

Circle the letters that have parallel line segments.

Question 11.

Answer:

Explanation:
Two lines are said to be parallel when they do not meet at any point in a plane.
Letters F, H, E, I, Z, N and M have parallel lines and are circled.
Letters V, A and T hand no parallel lines.

Name all the pairs of parallel line segments in each figure.

Example

Segments AB and ED

Question 12.

Answer:
Segments FG and JI

Explanation:
Two lines are said to be parallel when they do not meet at any point in a plane.
So, Segments FG and JI are paraell.

Question 13.

Answer:

Segments PK and NM
Segments LM and PO
Segments KL and ON
Explanation:
Parallel Lines or parallel Segments are always the same distance apart, they will never meet.
So, the above all are parallel.

Question 14.

Answer:
Segments RQ and TS

Explanation:
Two lines are said to be parallel when they do not meet at any point in a plane.
So, Segments RQ and TS are paraell.

Identify and name a pair of parallel line segments on each object.

Question 15.

Answer:
Segments AB and FE
Segments BC and ED
Segments AF and BE
Segments CD and BE

Explanation:
Parallel Lines or parallel Segments are always the same distance apart, they will never meet.
So, the above all are parallel.

Question 16.

Answer:

Segments RX and WV
Segments WV and TU
Segments WT and VU
Segments RS and WT
Segments WT and VU
Explanation:
Parallel Lines or parallel Segments are always the same distance apart, they will never meet.
So, the above all are parallel.

Carry out this activity.

Question 17.
Think of two objects that have parallel line segments. Use the Internet to find pictures of these objects. Print and paste them below. Use a colored pencil to trace a pair of parallel line segments on each object.

Answer:
YOU can observe parallel line segments on each object.

Explanation:
Parallel Lines or parallel Segments are always the same distance apart, they will never meet.
So, the above all are parallel.

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 17 Practice 3 Perpendicular Lines provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 17 Practice 3 Answer Key Perpendicular Lines

Guess if the lines are perpendicular. Use a ruler to check your guess.

Question 1.

Answer:
The lines are perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the wx and yz is 90 degrees.

Question 2.

Answer:
The lines are not perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the pq and rs is greater then 90 degrees.

Question 3.

Answer:
The lines are not perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the ab and cd is greater then 90 degrees.

Question 4.

Answer:
The lines are perpendicular and the angle between the ij and kl is 90 degrees

If the intersection between the two line segment is at a right angle, then the two lines are perpendicular,

Question 5.

Answer:
The lines are not perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the ab and cd is greater then 90 degrees.

Question 6.

Answer:
The lines are perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the pq and rs is 90 degrees.

Check (✓) the box if the lines are perpendicular.

Answer:

Explanation:
From the above figures we can come to conclusion that figures 1, 4 and 6 are parallel lines and
figures 2,3 and 5 are not parallel lines.

Use a ruler to check for perpendicular lines. Use a colored pencil to trace a pair of perpendicular lines in each figure.

Question 7.

Answer:
The lines are perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the wx and yz is 90 degrees.

Question 8.

Answer:
The lines are perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the pq and rs is 90 degrees.

Question 9.

Answer:
The lines are perpendicular.

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the pq and rs is 90 degrees.

Question 10.

Answer:
The lines are perpendicular

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the angle between the ij and kl is 90 degrees.

Circle the letters that have perpendicular line segments.

Question 11.

Answer:

Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
So, the letters T,L,E,H,F are perpendicular line segmests.

Name all the pairs of perpendicular line segments in each figure.

Example

Segments AB and BC

Question 12.

Answer:

The pairs of perpendicular line segments
Segments RQ and QP
Segments OP and ON
Segments MN and MR
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
The colors of lines indicate different pairs of line segments.

Question 13.

Answer:
The pairs of perpendicular line segments are:
Segments AB and AG
Segments AB and BC
Segments FE and DE
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
The colors of lines indicate different pairs of line segments.

Question 14.

Answer:
The pairs of perpendicular line segments are:
Segments MT and TS
Segments RS and TS
Segments OP and PQ
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.
The colors of lines indicate different pairs of line segments.

Identify and name a pair of perpendicular line segments on each object.

Question 15.

Answer:
A pair of perpendicular line segments on each object are,
AF and FE
BE and ED
CD and DE are a pair of perpendicular line segments.
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.

Question 16.

Answer:
A pair of perpendicular line segments on Encyclopedia are,
RS and RX
SV and VX
SV and VU are a pair of perpendicular line segments.
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.

Carry out this activity.

Question 17.
Think of two objects that have perpendicular line segments. Use the Internet to find pictures of these objects. Print and paste them below. Use a colored pencil to trace a pair of perpendicular line segments on each object.

Answer:
A pair of perpendicular line segments on objects are,
AB and ET
CE and ET
LM and mj
LN and NK
are a pair of perpendicular line segments.
Explanation:
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular.

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 18 Two-Dimensional Shapes provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 18 Answer Key Two-Dimensional Shapes

Put on Your Thinking Cap!

Challenging Practice

Question 1.
Copy the figure on a dot paper. Cut it out and rearrange the shapes in the figure to form a square.

Answer:

Explanation:
Cut the given figure for re arrange, and color it as shown in the above picture
place big triangles as number 1 & 2 colored red and blue, now half of your figure is completed
now for second half of place 3 at any one corner such that you can easily fix red small pictures
A Square is a regular quadrilateral or polygon.
which has all the four sides of equal length, four vertices and,
four angles with right angle triangles.

Question 2.
Study the pattern to find the rule. Then draw the missing shape.

Answer:

Explanation:
The pattern is Turn or Rotation.
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

Put On Your Thinking Cap!

Problem Solving

Question 1.
Look at the repeated pattern.
a. Check the box that shows the next shape.

Answer:
3rd pattern

Explanation:
The image is rotated in clockwise direction from horizontal axis to vertical axis,
such that the image rotates clockwise and the image resembles the same.

b. Check the box that shows the tenth shape.

Answer:
4th pattern

Explanation:
The image is rotated in clockwise direction from horizontal axis to vertical axis,
such that the image rotates clockwise and the image resembles the same.

Question 2.
Describe the movement shown by the shapes.
Answer:
The shapes are moving in the clock wise direction.
Explanation:
The image is rotated in clockwise direction from horizontal axis to vertical axis,
such that the image rotates clockwise and the image resembles the same.

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 19 Shapes and Patterns detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 19 Answer Key Shapes and Patterns

Math Journal

This pattern is made with plane shapes. Circle the mistake in the pattern. Name the correct shape. Then draw the repeating pattern unit.

The correct solid shape is a ___________.
Answer:

Explanation:
I drew a circle around the shape that is mistake in the pattern
I drew the repeating pattern unit
The correct solid shape is a  trapezium.

This pattern is made with plane shapes. Circle the mistake in the pattern. Name the correct shape. Then draw the repeating unit.

The correct solid shape is a ___________.
Answer:

Explanation:
I drew a circle around the shape that is mistake in the pattern
I drew the repeating pattern unit
The correct solid shape is a  rectangular prism.

Put On Your Thinking Cap!

Challenging practice

Use plane shapes to make a pattern

Question 1.
using shapes of different types.
Answer:

Explanation:
I made a pattern using a circle, rectangle and a hexagon
I repeated the group of 3 shapes 3 times.

Question 2.
using the same shape of different colors.
Answer:

Explanation:
I made a pattern using red and yellow squares
I repeated the each colored square alternatively for 3 times.

Question 3.
by turning the shape.
Answer:

Explanation:
I made a patter using rectangle
I turned the shape to create the pattern
I repeated the group of shapes 3 times.

Chapter Review/Test

Vocabulary

Fill in the blanks with words from the box.

hexagon
trapezoid
pattern
turning

Question 1.
You can form a repeating __________ using different shapes, colors, sizes, and by __________ the shapes.
Answer:
You can form a repeating pattern using different shapes, colors, sizes, and by turning the shapes.

Question 2.
A __________ has six sides.
Answer:
A hexagon has six sides.

Question 3.
A __________ is four-sided like the square and the rectangle.
Answer:
A trapezoid is four-Sided like the square and the rectangle.

Concepts and Skills

Match the shape to its name.

Question 4.

Answer:
b. cylinder

Explanation:
The above shape is a cylinder
It has a curved face and 2 flat faces.

Question 5.

Answer:
a. pentagon

Explanation:
The above shape is a pentagon
It has 5 sides.

Question 6.

Answer:
d. pyramid

Explanation:
The above shape is a pyramid
It has 5 faces.

Question 7.

Answer:
e. rectangular prism

Explanation:
The above shape is a rectangular prism
It has 6 faces.

Question 8.

Answer:
c. hexagon

Explanation:
The above given shape is a hexagon
It has six sides.

Question 9.

Answer:
f. trapezoid

Explanation:
The above shape is a trapezoid
It has 2 parallel side.

a. pentagon
b. cylinder
c. hexagon
d. pyramid
e. rectangular prism
f. trapezoid

Use this shape to make another bigger shape. Write how many of this shape you used. Name the shape you made.

Question 10.

Answer:

Explanation:
I used triangle and created another bigger shape
I used 6 triangles to make the bigger shape
I made a hexagon.

Draw lines to separate this rectangle into several copies of the same smaller shape.

Question 11.

Answer:

Explanation:
I drew some lines to separate this rectangles into several copies of the same smaller shape
I made 8 smaller rectangles by drawing 4 lines.

Copy the shape onto the dot grid. Circle one of the angles of the shape.

Question 12.

Answer:

Explanation:
I copied the above given shape in the dot grid in the right
I drew a circle around 1 of the angles of the shape
I drew a circle on the right angle.

Write the number of plane shapes that make up this figure.

Question 13.

Answer:

Explanation:
3 plane shapes make up this figure
2 rectangles and 1 triangle make the shape in the picture.

Write the number of solid shapes that make up this model.

Question 14.

Answer:

Explanation:
12 plane shapes make up this figure
They are 6 cubes, 2 rectangular prisms, 2 cones, 1 sphere and 1 cylinder.

Draw the next figure in each pattern.

Question 15.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
The above pattern is made of triangles and rectangles of different sizes
I drew a big triangle to complete the patter.

Question 16.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
There are some circles with change in direction that make the pattern
I drew the next shape to complete the pattern.

Complete the pattern. Circle the correct solid or model.

Question 17.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I drew a circle for the correct shape among the 2 shapes that complete the pattern.

Question 18.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I drew a circle for the correct shape among the 2 shapes that complete the pattern.

Problem Solving

Look at the pattern. Draw what comes next.

Question 19.

Answer:

Explanation:
The above pattern is an increasing pattern
I drew 4 triangles together to show the next shape in the pattern.

Question 20.
Susan wants to make a hexagon using the least number of one shape.
a. Which can she use?
Answer:

Explanation:
Susan wants to make a hexagon using the least number of one shape
He can make a hexagon with trapezoids and with triangles
The least number of shapes he can use is using trapezoids.

b. How many of this shape will she use?
Answer:
She will use 2 trapezoids to make a hexagon.

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 19 Practice 3 Making Patterns detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 19 Practice 3 Answer Key Making Patterns

Look at the pattern. Draw what comes next.

Example

Question 1.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
Circles of different sizes and colors are made as a pattern
I drew a small size colored circle to complete the pattern.

Question 2.

Answer:

Question 3.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
The shape pattern has a triangle, square and a circle
So, i drew a triangle to complete the pattern.

Circle the correct shapes or figures made of shapes to complete the pattern.

Example

Question 4.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
Circles of different sizes and colors are made as a pattern
I drew a small size colored circle to complete the pattern.

Question 5.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
Circles of different sizes and cylinders are made as a pattern
I drew a big size  circle to complete the pattern.

Question 6.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
Triangular pieces of different directions are made as a pattern
I circled the shape that is correct among the 2 to complete the pattern.

Question 7.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 2 to complete the pattern.

Circle the correct shapes or figures made of shapes to complete the pattern.

Question 8.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 3 to complete the pattern.

Question 9.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 2 to complete the pattern.

Question 10.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 3 to complete the pattern.

Circle the correct shapes or figures made of shapes to complete the pattern.

Question 11.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 3 to complete the pattern.

Question 12.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shape that is correct among the 3 to complete the pattern.

Question 13.

Answer:

Explanation:
Shape pattern occur when a group of shapes are repeated again and again
I circled the shapes that are correct among the 2 to complete the pattern.