Hillary

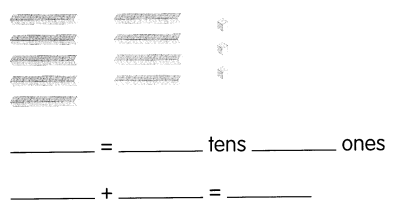
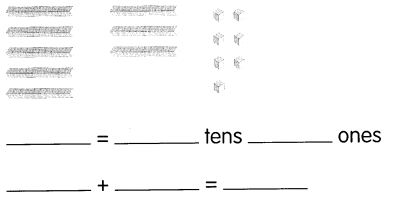
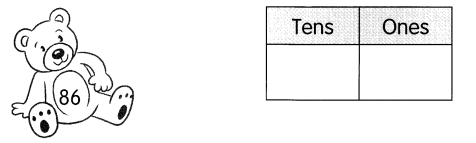
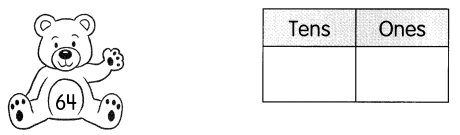
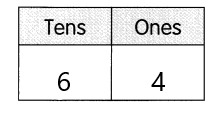
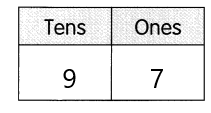
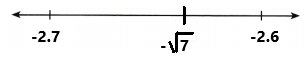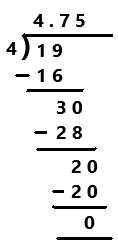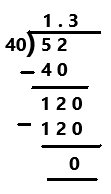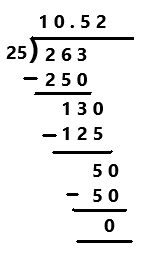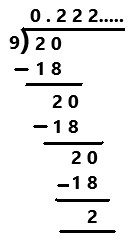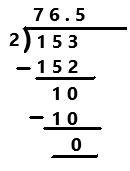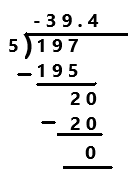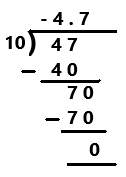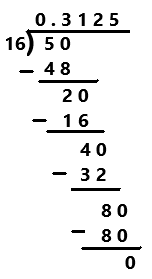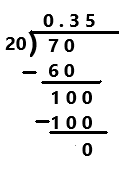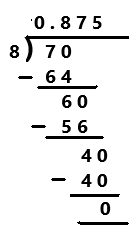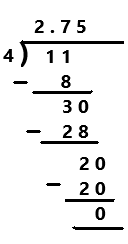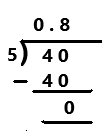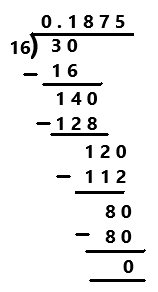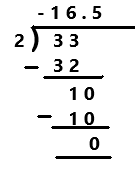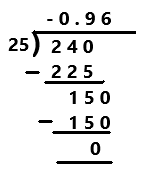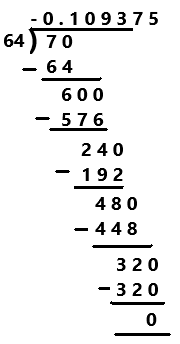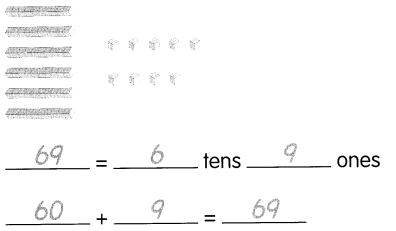Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 2 Lesson 2.1 Adding Integers to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 2 Lesson 2.1 Answer Key Adding Integers

Math in Focus Grade 7 Chapter 2 Lesson 2.1 Guided Practice Answer Key

Copy and complete.

Question 1.
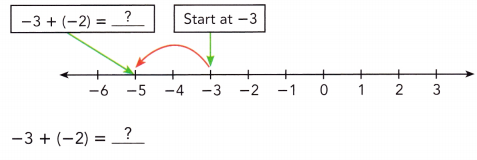
Evaluate -3 + (-2).
Method 1
Use a number line to model the sum of two negative integers.

Answer:

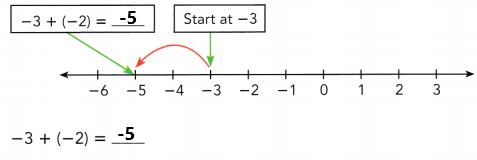
Start at -3. Then add -2. Because you are adding a negative integer, -2, you make a jump of 2 to the left.

Method 2
Use absolute values to find the sum of two negative integers.
|-3| = Write the absolute value of each integer.
|-2| =
|-3| + |-2| = + Add the absolute values.
= Simplify.
-3 + (-2) = Use the common sign, a sign, for the sum.
Answer:
|-3| = 3
|-2| = 2
|-3| + |-2| = 3 + 2
= 5
-3 + (-2) = -5 Used the common sign, a negative sign, for the sum.

Question 2.
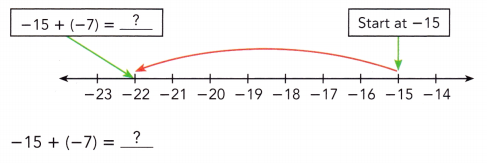
Evaluate -15 + (-7).
Method 1
Use a number line to model the sum of two negative integers.

Answer:

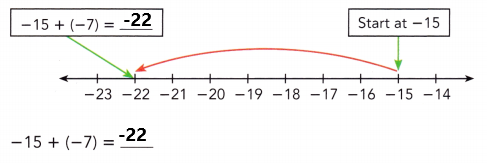
Start at -15 then add -7. Because we are adding a negative integer, -7, we make a jump of 7 to the left.
Method 2
Use absolute values to find the sum of two negative integers.
|-15| =
|-7| =
|-15| + |-7| = +
=
-15 + (-7) =
Answer:
|-15| = 15
|-7| = 7
|-15| + |-7| = 15 + 7
= 22
-15 + (-7) = -22

Evaluate each sum.

Question 3.
9 + (-9)
Answer:
9 – 9 = 0
Explanation:
Perform addition operation on above two numbers 9 and -9. Add 9 with -9 the sum is o.

Question 4.
-21 + 21
Answer:
-21 + 21 = 0
Explanation:
Perform addition operation on above two numbers -21 and 21. Add -21 with 21 the sum is o.

Hands-On Activity

Materials:

• counters

Find the sum of integers with different signs.

Work in pairs.

A zero pair has a value of zero.
(+1) + (-1) = (-1) + (+1)
= 0
Removing a zero pair does not change the value of an expression. For example:
(+1) + (-1) + 2 = 2 because
(+1) + (-1) + 2 = 0 + 2
= 2

Step 1.
Use counters to model and find the sum of two integers with different signs.
a) Evaluate 3 + (-2).

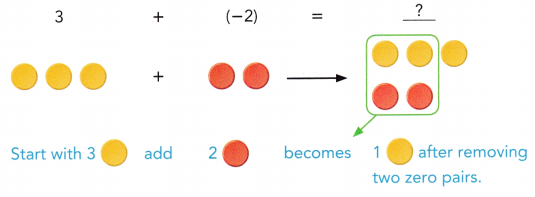
Answer:

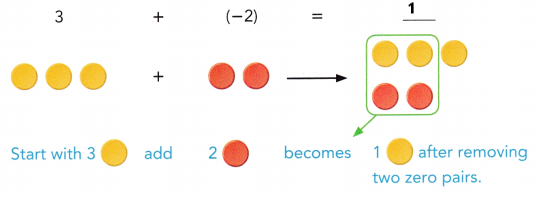
A zero pair has a value of zero.
(+2) + (-2) = (-2) + (+2)
= 0
Removing a zero pair does not change the value of an expression.
(+2) + (-2) + 1 = 1 because
(+2) + (-2) + 1 = 0 + 1
= 1

b) Evaluate (-3) + 2

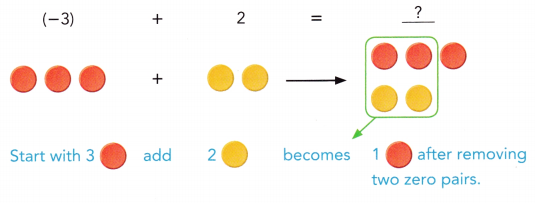
Answer:

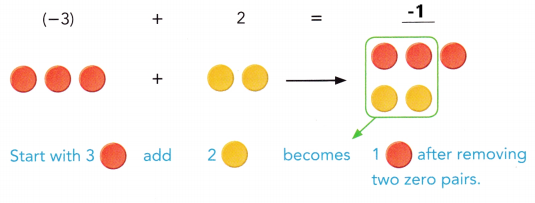
A zero pair has a value of zero.
(+2) + (-2) = (-2) + (+2)
= 0
Removing a zero pair does not change the value of an expression.
(-2) + (+2) + (-1)  = -1 because
(-2) + (+2) + (-1) = 0 + (-1)
= -1

Step 2.
Use counters to model and find each sum.
a) 7 + (-2) and (-7) + 2
Answer:

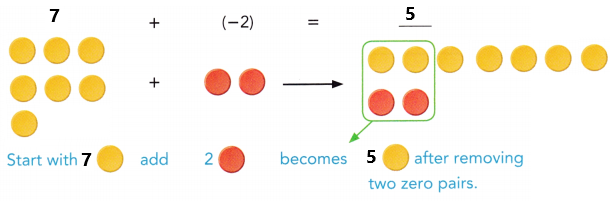
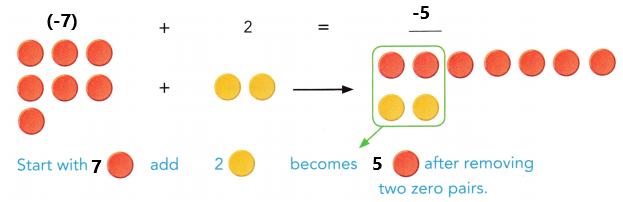
b) (-8) + 5 and 8 + (-5)
Answer:

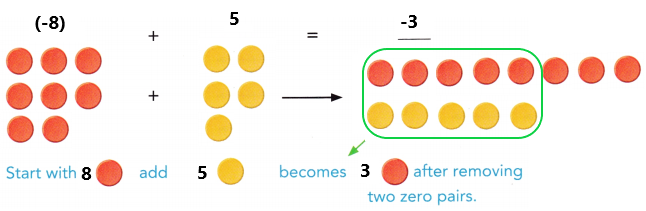
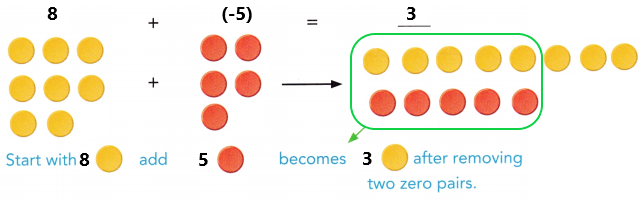
Math Journal
Explain how to add two integers with different signs. How are the absolute values of the addends related to the sum?

Evaluate each sum.

Question 5.
-10 + 3
Answer:
-10 + 3 = -7
Explanation:
Perform addition operation on above two numbers -10 and 3 the sum is -7.

Question 6.
-9 + 2
Answer:
-9 + 2 = -7
Explanation:
Perform addition operation on above two numbers -9 and 2 the sum is -7.

Question 7.
11 + (-23)
Answer:
11 + (-23) = -12
Explanation:
Perform addition operation on above two numbers 11 and -23 the sum is -12.

Evaluate each sum.

Question 8.
10 + (-3) + 6
Answer:
10 + (-3) + 6
= 16 + (-3)
= 13
Explanation:
Perform addition operation on above numbers. First add 10 with 6 the sum is 16. Next add the sum 16 with -3 the sum is 13.

Question 9.
-7 + (-23) + 15
Answer:
-7 + (-23) + 15
= -30 + 15
= -15
Explanation:
Perform addition operation on above numbers. First add -7 with -23 the sum is -30. Next add the sum -30 with 15 the sum is -15.

Solve.

Question 10.
A submarine ¡s at 400 feet below sea level. If it ascends 150 feet and then descends 320 feet, how far is ¡t above or below sea level?

You can think of the submarine ascending as an adding a positive integer, and descending as adding a negative integer. So, the verbal description can be translated as -400 + 150 + (-320).

Answer:
-400 + 150 + (-320) = -570
A submarine is 570 feet below sea level.
Explanation:
The submarine ascending as an adding a positive integer, and descending as adding a negative integer. A submarine ¡s at 400 feet below sea level. It ascends 150 feet and then descends 320 feet. Add -400 with 150 and -320 the sum is -570 feet.

Math in Focus Course 2A Practice 2.1 Answer Key

Evaluate each sum using a number line.

Question 1.
-3 + (-9)
Answer:

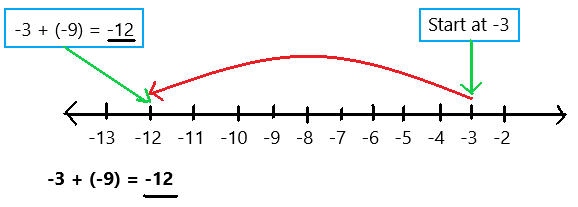
Explanation:
To evaluate the sum of two negative integers use a number line as we can observe in the above image. Start at -3. Then add -9. Because i am adding a negative integer, -9, I make a jump of 9 to the left. The sum of two negative integers is -12.

Question 2.
-8 + (-4)
Answer:

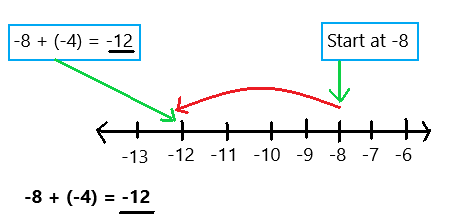
Explanation:
To evaluate the sum of two negative integers use a number line as we can observe in the above image. Start at -8. Then add -4. Because i am adding a negative integer, -4, I make a jump of 4 to the left. The sum of two negative integers is -12.

Question 3.
7 + (-7)
Answer:

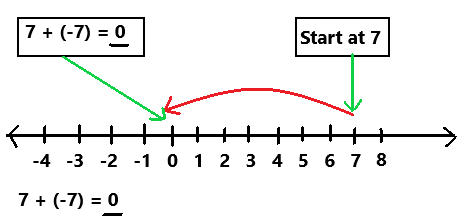
Explanation:
To evaluate the sum of two integers use a number line as we can observe in the above image. Start at 7. Then add -7. Because i am adding a negative integer, -7, I make a jump of 7 to the left. The sum of two integers is 0.

Question 4.
-9 + 9
Answer:

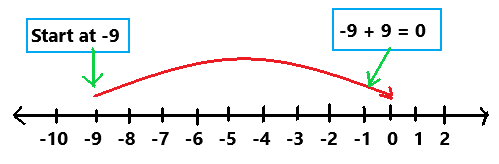
Answer:
To evaluate the sum of two integers use a number line as we can observe in the above image. Start at -9. Then add 9. Because i am adding a positive integer, 9, I make a jump of 9 to the right. The sum of two integers is 0.

Question 5.
-10 + 6
Answer:

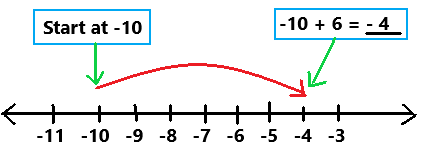
Explanation:
To evaluate the sum of two integers use a number line as we can observe in the above image. Start at -10. Then add 6. Because i am adding a positive integer, 6, I make a jump of 6 to the right. The sum of two integers is -4.

Question 6.
-17 + 9
Answer:

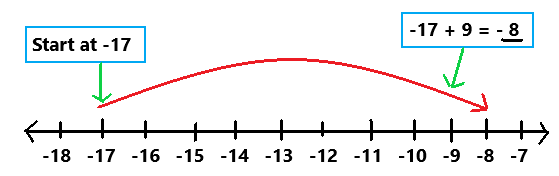
Explanation:
To evaluate the sum of two integers use a number line as we can observe in the above image. Start at -17. Then add 9. Because i am adding a positive integer, 9, I make a jump of 9 to the right. The sum of two integers is -8.

Evaluate each sum using the absolute values.

Question 7.
-23 + (-9)
Answer:
Use absolute values to find the sum of above two negative integers.
|-23| = 23
The absolute value of -23 is 23.
|-9| = 9
The absolute value of -9 is 9.
Add the absolute values.
|-23| + |-9| = 23 + 9
= 32
-23 + (-9) = -32
Use the common sign, a negative sign, for the sum.

Question 8.
-11 + (-34)
Answer:
Use absolute values to find the sum of above two negative integers.
|-11| = 11
The absolute value of -11 is 11.
|-34| = 34
The absolute value of -34 is 34.
Add the absolute values.
|-11| + |-34| = 11 + 34
= 45
-11 + (-34) = -45
Use the common sign, a negative sign, for the sum.

Question 9.
-15 + (-7)
Answer:
Use absolute values to find the sum of above two negative integers.
|-15| = 15
The absolute value of -15 is 15.
|-7| = 7
The absolute value of -7 is 7.
Add the absolute values.
|-15| + |-7| = 15 + 7
= 22
-15 + (-7) = -22
Use the common sign, a negative sign, for the sum.

Question 10.
12 + (-18)
Answer:
Use absolute values to find the sum of above two integers.
|12| = 12
The absolute value of 12 is 12.
|-18| = 18
The absolute value of -18 is 18.
Add the absolute values.
|12| + |-18| = 12 + 18
= 30
12 + (-18) = -6
Use the common sign, a negative sign, for the sum.

Question 11.
-40 + 26
Answer:
Use absolute values to find the sum of above two integers.
|-40| = 40
The absolute value of -40 is 40.
|26| = 26
The absolute value of 26 is 26.
Add the absolute values.
|-40| + |26| = 40 + 26
= 66
-40 + 26 = -14
Use the common sign, a negative sign, for the sum.

Question 12.
-75 + 19
Answer:
Use absolute values to find the sum of above two integers.
|-75| = 75
The absolute value of -75 is 75.
|19| = 19
The absolute value of 19 is 19.
Add the absolute values.
|-75| + |19| = 75 + 19
=94
-75 + 19 = -56
Use the common sign, a negative sign, for the sum.

Evaluate each sum.

Question 13.
-8 + 4 + 5
Answer:
-8 + 4 + 5
= -8 + 9
= 1
Explanation:
Perform addition operation on above numbers. First add 4 with 5 the sum is 9. Next add -8 with 9 the sum is 1.

Question 14.
5 + (-10) + (-6)
Answer:
5 + (-10) + (-6)
= -5 + (-6)
= -11
Explanation:
Perform addition operation on above numbers. First add 5 with -10 the sum is -5. Next add -5 with -6 the sum is -11.

Question 15.
-6 + (-8) + (-12)
Answer:
-6 + (-8) + (-12)
= -14 + (-12)
= -26
Explanation:
Perform addition operation on above numbers. First add -6 with -8 the sum is -14. Next add -14 with -12 the sum is -26.

Question 16.
-13 + (-17) + 7
Answer:
-13 + (-17) + 7
= -30 + 7
= -23
Explanation:
Perform addition operation on above numbers. First add -13 with -17 the sum is -30. Next add -30 with 7 the sum is -23.

Question 17.
-20 + 16 +(-7)
Answer:
-20 + 16 +(-7)
= -4 + (-7)
= -11
Explanation:
Perform addition operation on above numbers. First add -20 with 16 the sum is -4. Next add -4 with -7 the sum is -11.

Question 18.
-11 + (-8) + 14
Answer:
-11 + (-8) + 14
= -19 + 14
= -5
Explanation:
Perform addition operation on above numbers. First add -11 with -8 the sum is -19. Next add -19 with 14 the sum is -5.

Solve. Show your work.

Question 19.
The temperature is originally recorded as -4°F. What will the temperature be if the temperature rises 20°F?
Answer:
-4°F + 20°F = 16°F
Explanation:
The temperature is originally recorded as -4°F. The temperature rises to 20°F. Add -4°F with 20°F the sum is 16°F. The temperature is 16°F.

Question 20.
Mr. Lawson parked his car in a parking garage 33 feet below street level. He then got in an elevator and went up 88 feet to his office. How far above street level is his office?
Answer:

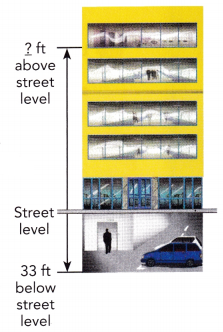
Answer:
88 – 33 = 55 feet
His office is 55 feet above street level.
Explanation:
Mr. Lawson parked his car in a parking garage 33 feet below street level. He then got in an elevator and went up 88 feet to his office. Subtract 33 feet below street level from 88 feet the difference is 55 feet. His office is 55 feet above street level.

Question 21.
A hiker starts hiking in Death Valley at an elevation of 143 feet below sea level. He climbs up 400 feet in elevation. What is his new elevation relative to sea level?
Answer:
A hiker starts hiking in Death Valley at an elevation of 143 feet below sea level. Below sea level is represented with negative number which is -143 feet.
He climbs up 400 feet in elevation. The word ‘climbs up’ represents positive number which is 400 feet.
– 143 feet + 400 feet = 257 feet
His new elevation is 257 feet above seal level.

Question 22.
Elizabeth was playing a board game with her friends. On her first turn, she moved 6 spaces forward. On her second turn, she moved another 5 spaces forward. On her third turn, she moved 4 spaces backward. How many spaces forward or backward from her starting point was she after her third turn?
Answer:
6 + 5 – 4
= 11 – 4
= 7
After her third turn Elizabeth moved 7 spaces forward from her starting point.
Explanation:
Elizabeth was playing a board game with her friends. On her first turn, she moved 6 spaces forward. Forward spaces are represented with positive number. On her second turn, she moved another 5 spaces forward. Forward spaces are represented with positive number. Add 6 with 5 the sum is 11. On her third turn, she moved 4 spaces backward. Backward spaces are represented with negative number. Subtract 4 from 11 the difference is 7. After her third turn Elizabeth moved 7 spaces forward from her starting point.

Question 23.
In the U.S. Open Golf Tournament, each qualifying golfer plays four rounds. The score for a round is recorded as positive (over par) or negative (under par). If a golfer scores -4, 6, 3, and -2 in the four rounds, what is the golfer’s total score for the tournament?
Answer:
The golfer scores -4, 6, 3, and -2 in four rounds.
-4 + 6 + 3 -2
= 9 – 6
= 3
The golfer’s total score for the tournament is 3.

Question 24.
Math Journal
In a game, all scores with even numbers are recorded as positive numbers. Odd numbers are recorded as negative numbers. Explain how to find David’s total score in this game if his individual scores during the game are 9, 12, 7, 18, and 19.
Answer:
The individual scores during the game are 9, 12, 7, 18, and 19.
Here the scores with even numbers are recorded as positive numbers.
The scores with Odd numbers are recorded as negative numbers.
The scores are -9, 12, -7, 18, -19
David’s total score is calculated by adding the given scores.
– 9 + 12  -7 + 18 – 19
= 30 – 9 – 7 – 19
= 30 – 35
= -5
David’s total score in this game is -5.

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 14 Practice 2 Reading and Writing Time detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 14 Practice 2 Answer Key Reading and Writing Time

Write the time in words.

Example

Question 1.

Answer:

three fifteen or 15 minutes after 3.

Question 2.

Answer:

eleven forty or 40 minutes after eleven.

Question 3.

Answer:

one twenty-five or 25 minutes after 1

Question 4.

Answer:

three thirty five or 35 minutes after 3

Question 5.

Answer:

eight fifty-five or 55 minutes after 8.

Write the time

Example

Question 6.

The time is _____________.
Answer:

The time is 1:45

Question 7.

The time is _____________.
Answer:

The time is 2:00

Question 8.

The time is _____________.
Answer:

The time is 6:20

Question 9.

The time is _____________.
Answer:

The time is 9:05

Question 10.

The time is _____________.
Answer:

The time is 2:55

Draw the minute hand to show the time.

Example

The time is 3:55.

Question 11.

The time is 6:30.
Answer:

Question 12.

The time is 10:15.
Answer:

Question 13.

The time is 8:00.
Answer:

Question 14.

The time is 12:40.
Answer:

Question 15.

The time is 9:05.
Answer:

Draw the hour hand to show the time.

Example

The time is 10:00.

Question 16.

The time is 11:30.
Answer:

Question 17.

The time is 7:15.
Answer:

Question 18.

The time is 4:20.
Answer:

Question 19.

The time is 2:50.
Answer:

Question 20.

The time is 3:40.
Answer:

Draw the hands to show the time.

Example

The time is 7:15.

Question 21.

The time is 4:30.
Answer:

Question 22.

The time is 1:20.
Answer:

Question 23.

The time is 9:25.
Answer:

Question 24.

The time is 7:00.
Answer:

Question 25.

The time is 9:50.
Answer:

Draw the hands to show the time. Then write the time in words.

Example

Question 26.

Answer:

five ten or 10 minutes after 5

Question 27.

Answer:

eleven forty or 40 minutes after 11

Question 28.

Answer:

six fifty five or 55 minutes after 6

Question 29.

Answer:

one twenty-five or 25 minutes after 1

Question 30.

Answer:

twelve-fifteen or 15 minutes after 12

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 14 Practice 1 The Minute Hand detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 14 Practice 1 Answer Key The Minute Hand

Question 1.
Fill in the boxes with the number of minutes.

Answer:

Fill in the blanks.

Example

Question 2.

The minute hand points to ___________ minutes.
Answer:

The minute hand points to 35 minutes.

Question 3.

The minute hand points to ___________ minutes.
Answer:

The minute hand points to 20 minutes.

Question 4.

The minute hand points to ___________ minutes.
Answer:

The minute hand points to 55 minutes.

Write the time.

Question 5.

Answer:

3 o’clock                                                      5 minutes after 3 o’clock

Question 6.

Answer:

7 o’clock                                                20 minutes after 7 o’clock

Question 7.

Answer:

10 o’clock                                                     45 minutes after 10 o’clock

Draw the minute hand to show the time.

Question 8.
15 minutes after 4 o’clock

Answer:

Question 9.
40 minutes after 6 o’clock

Answer:

Question 10.
50 minutes after 1 o’clock

Answer:

Question 11.
35 minutes after 10 o’clock

Answer:

This handy Math in Focus Grade 2 Workbook Answer Key Chapter 15 Multiplication Tables of 3 and 4 detailed solutions for the textbook questions.

Math in Focus Grade 2 Chapter 15 Answer Key Multiplication Tables of 3 and 4

Math Journal

These items are sold in a supermarket. Use the items to write a multiplication story.

Example
I want to buy 4 boxes of cereal.
I will have to give the cashier $16.

Story
__________________
Answer:

I want to buy cracked which costs $3

I want to buy cereal which costs $4.

Put On Your Thinking Cap!

Challenging Practice

Question 1.
Steve starts reading a book on page 7. He reads the book for 4 days. He reads 3 pages each day. Which page will Steve stop at on the 4th day?
(Hint: Use a diagram to help you solve.)
Answer:

Given,

Steve starts reading a book on page 7.

He reads the book for 4 days.

He reads 3 pages each day.

So, 4 x 3 = 12

12 + 7 = 19

Therefore, on the 4th day, steve will stop on the 19th page.

Question 2.
The music teacher is selecting children to sit in the front row at a concert. 100 children are given numbers 1 to 100. The teacher first picks the child with the number 3. He then skip-counts by tens to pick the other children. What are the numbers of the other children who are picked?
The numbers are ___________________
Answer:

Given,

The music teacher is selecting children to sit in the front row at a concert.

100 children are given numbers 1 to 100.

The teacher first picks the child with the number 3.

He then skip-counts by tens to pick the other children.

Put On Your Thinking Cap!

Problem Solving

Solve the riddle.

Question 1.
I am a two-digit number. I am more than 20 but less than 30. I can be found in both the multiplication tables of 3 and 4. What number am I?
Answer:

Given,

I am a two-digit number.

I am more than 20 but less than 30.

I can be found in both the multiplication tables of 3 and 4.

Let the number be a

20 < a > 30

the numbers that are both multiple of 3 and 4 and between 20 and 30 is are 24 only ( 3 x 8 = 4 x 6 )

Therefore, the number is 24.

Chapter Review/Test

Vocabulary

Fill in the blanks with words from the box.

skip-counting
dot paper
related multiplication facts

Question 1.

____________ is fun!
Answer:

Question 2.
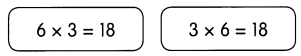are examples of _____________.
Answer:

Concepts and Skills

Skip count to find the missing numbers.

Question 3.
9 × 3 = ____________
Answer:

Question 4.
___________ × 3 = 24
Answer:

Question 5.
_________ × 4 = 16
Answer:

Question 6.
_________ × 4 = 36
Answer:

Find the missing numbers.

Question 7.
8 groups of 3 = __________ × 3
= ___________
Answer:

Question 8.
7 groups of 4 = ___________ × 4
= ___________
Answer:

Use dot paper to find the missing numbers.

Question 9.
6 × 4 = 5 groups of 4 + ___________ group of 4
= ___________ + 4
= ___________
Answer:

Problem Solving

Use skip-counting or dot paper to solve.

Question 10.
Caleb ties sets of 3 medals with a piece of ribbon. He ties 10 sets of medals. How many medals does Caleb have in all?
Answer:

Use related multiplication facts to solve.

Question 11.
Gail has 32 star-shaped key chains. She puts 4 key chains equally into some boxes. How many boxes are there?
Answer:

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.3 Introducing Irrational Numbers to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.3 Answer Key Introducing Irrational Numbers

Math in Focus Grade 7 Chapter 1 Lesson 1.3 Guided Practice Answer Key

Hands-On Activity

Materials:

• paper
• ruler
• scissors

Find the value of \(\sqrt{2}\) using a square.

Work in pairs.

Step 1.
Draw a square that has a length of 2 inches on a piece of paper. Then cut out the square.

Step 2.
Find the area of the square (square A).

Step 3.
Fold the four vertices of square A towards the center to form square B as shown below.

Step 4.
State how the areas of square A and square B are related. State the area of square B. How can you represent the length of a side of square B?

Step 5.
Using your answer in step 4, find the length of a side of square B with a calculator. Round your answer to 2 decimal places.

Math Journal
Place an edge of square B alongsi& a ruler to measure its length. Explain why the reading from the ruler is different from the answer in step 5.

Copy and complete.

Question 1.
Graph \(\sqrt{5}\) on the number line using rational approximations.
Which two whole numbers is \(\sqrt{5}\) between? Justify your reasoning. Using a calculator, \(\sqrt{5}\) = .
Graph an interval where \(\sqrt{5}\) is located.
The value of \(\sqrt{5}\) with two decimal places is
is closer to than to . So, \(\sqrt{5}\) is located closer to .

By using an approximate value of \(\sqrt{5}\), locate \(\sqrt{5}\) on the number line.

Answer:
The \(\sqrt{5}\) is between two whole numbers. The two whole numbers are 2 and 3.
By using calculator \(\sqrt{5}\) = 2.236067977….
The value of \(\sqrt{5}\) with two decimal places is 2.24.
The decimal 2.24 is closer to 2.2 than to 2.3.
So, \(\sqrt{5}\) is located closer to 2.2.

By using an approximate value of \(\sqrt{5}\),  located  \(\sqrt{5}\) on the number line as we can observe in the below image.

Copy and complete.

Question 2.
Graph –\(\sqrt{2}\) on the number line using rational approximations.
Which two integers is –\(\sqrt{2}\) between? Justify your reasoning. Using a calculator, –\(\sqrt{2}\) = .
Graph an interval where –\(\sqrt{2}\) is located.
The value of –\(\sqrt{2}\) with two decimal places is ? .
is closer to than to . So, –\(\sqrt{2}\) is located closer to ?

By using an approximate value of –\(\sqrt{2}\), locate –\(\sqrt{2}\) on the number line.

Answer:
The –\(\sqrt{2}\) is between two whole numbers. The two whole numbers are -1 and -2.
By using calculator –\(\sqrt{2}\) = -1.414213562…..
The value of –\(\sqrt{2}\) with two decimal places is -1.41.
The decimal -1.41 is closer to -1.4 than to -1.5.
So, –\(\sqrt{2}\) is located closer to -1.4.

By using an approximate value of –\(\sqrt{2}\),  located  –\(\sqrt{2}\) on the number line as we can observe in the below image.

Solve.

Question 3.
Graph –\(\sqrt{7}\) on the number line using rational approximations.
Answer:
The –\(\sqrt{7}\) is between two whole numbers. The two whole numbers are -2 and -3.
By using calculator –\(\sqrt{7}\) = -2.645751311…..
The value of –\(\sqrt{7}\) with two decimal places is -2.64.
The decimal -2.64 is closer to -2.6 than to -2.7.
So, –\(\sqrt{7}\) is located closer to -2.6.
By using an approximate value of –\(\sqrt{7}\),  located  –\(\sqrt{7}\) on the number line as we can observe in the below image.

Math in Focus Course 2A Practice 1.3 Answer Key

Locate each positive irrational number on the number line using rational approximations. First tell which two whole numbers the square root is between.

Question 1.
\(\sqrt{3}\)
Answer:
The \(\sqrt{3}\) is between two whole numbers. The two whole numbers are 1 and 2.
By using calculator \(\sqrt{3}\) = 1.732050807….
The value of \(\sqrt{3}\) with two decimal places is 1.73.
The decimal 1.73 is closer to 1.7 than to 1.8.
So, \(\sqrt{3}\) is located closer to 1.7.

By using an approximate value of \(\sqrt{3}\),  the positive irrational number \(\sqrt{3}\) is located on the number line as we can observe in the above image.

Question 2.
\(\sqrt{7}\)
Answer:
The \(\sqrt{7}\) is between two whole numbers. The two whole numbers are 2 and 3.
By using calculator \(\sqrt{7}\) = 2.645751311….
The value of \(\sqrt{7}\) with two decimal places is 2.64.
The decimal 2.64 is closer to 2.6 than to 2.7.
So, \(\sqrt{7}\) is located closer to 2.6.

By using an approximate value of \(\sqrt{7}\),  the positive irrational number \(\sqrt{7}\) is located on the number line as we can observe in the above image.

Question 3.
\(\sqrt{11}\)
Answer:
The \(\sqrt{11}\) is between two whole numbers. The two whole numbers are 3 and 4.
By using calculator \(\sqrt{11}\) = 3.316624790….
The value of \(\sqrt{11}\) with two decimal places is 3.31.
The decimal 3.31 is closer to 3.3 than to 3.4.
So, \(\sqrt{11}\) is located closer to 3.3.

By using an approximate value of \(\sqrt{11}\),  the positive irrational number \(\sqrt{11}\) is located on the number line as we can observe in the above image.

Question 4.
\(\sqrt{26}\)
Answer:
The \(\sqrt{26}\) is between two whole numbers. The two whole numbers are 5 and 6.
By using calculator \(\sqrt{26}\) = 5.099019513….
The value of \(\sqrt{26}\) with two decimal places is 5.09.
The decimal 5.09 is closer to 5.1 than to 5.0.
So, \(\sqrt{26}\) is located closer to 5.1.

By using an approximate value of \(\sqrt{26}\),  the positive irrational number \(\sqrt{26}\) is located on the number line as we can observe in the above image.

Question 5.
\(\sqrt{34}\)
Answer:
The \(\sqrt{34}\) is between two whole numbers. The two whole numbers are 5 and 6.
By using calculator \(\sqrt{34}\) = 5.830951894….
The value of \(\sqrt{34}\) with two decimal places is 5.83.
The decimal 5.83 is closer to 5.8 than to 5.9.
So, \(\sqrt{34}\) is located closer to 5.8.

By using an approximate value of \(\sqrt{34}\),  the positive irrational number \(\sqrt{34}\) is located on the number line as we can observe in the above image.

Question 6.
\(\sqrt{48}\)
Answer:
The \(\sqrt{48}\) is between two whole numbers. The two whole numbers are 6 and 7.
By using calculator \(\sqrt{48}\) = 6.928203230….
The value of \(\sqrt{48}\) with two decimal places is 6.92.
The decimal 6.92 is closer to 6.9 than to 7.0.
So, \(\sqrt{48}\) is located closer to 6.9.

By using an approximate value of \(\sqrt{48}\),  the positive irrational number \(\sqrt{48}\) is located on the number line as we can observe in the above image.

Locate each negative irrational number on the number line using rational approximations. First tell which two integers the square root is between.

Question 7.
–\(\sqrt{5}\)
Answer:
The –\(\sqrt{5}\) is between two integers. The two integers are -2 and -3.
By using calculator –\(\sqrt{5}\) = -2.236067977…..
The value of –\(\sqrt{5}\) with two decimal places is -2.23.
The decimal -2.23 is closer to -2.2 than to -2.3.
So, –\(\sqrt{5}\) is located closer to -2.2.

By using an approximate value of –\(\sqrt{5}\), the negative irrational number –\(\sqrt{5}\) is located on the number line as we can observe in the above image.

Question 8.
–\(\sqrt{6}\)
Answer:
The –\(\sqrt{6}\) is between two integers. The two integers are -2 and -3.
By using calculator –\(\sqrt{6}\) = -2.449489742…..
The value of –\(\sqrt{6}\) with two decimal places is -2.44.
The decimal -2.44 is closer to -2.4 than to -2.5.
So, –\(\sqrt{6}\) is located closer to -2.4.

By using an approximate value of –\(\sqrt{6}\), the negative irrational number –\(\sqrt{6}\) is located on the number line as we can observe in the above image.

Question 9.
–\(\sqrt{17}\)
Answer:
The –\(\sqrt{17}\) is between two integers. The two integers are -4 and -5.
By using calculator –\(\sqrt{17}\) = -4.123105625…..
The value of –\(\sqrt{17}\) with two decimal places is -4.12.
The decimal -4.12 is closer to -4.1 than to -4.2.
So, –\(\sqrt{17}\) is located closer to -4.1.

By using an approximate value of –\(\sqrt{17}\), the negative irrational number –\(\sqrt{17}\) is located on the number line as we can observe in the above image.

Question 10.
–\(\sqrt{26}\)
Answer:
The –\(\sqrt{26}\) is between two integers. The two integers are -5 and -6.
By using calculator –\(\sqrt{26}\) = -5.099019513….
The value of –\(\sqrt{26}\) with two decimal places is -5.09.
The decimal -5.09 is closer to -5.1 than to -5.0.
So, –\(\sqrt{26}\) is located closer to -5.1.

By using an approximate value of –\(\sqrt{26}\), the negative irrational number –\(\sqrt{26}\) is located on the number line as we can observe in the above image.

Question 11.
–\(\sqrt{53}\)
Answer:
The –\(\sqrt{53}\) is between two integers. The two integers are -7 and -8.
By using calculator –\(\sqrt{53}\) = -7.280109889….
The value of –\(\sqrt{53}\) with two decimal places is -7.28.
The decimal -7.28 is closer to -7.3 than to -7.2.
So, –\(\sqrt{53}\) is located closer to -7.3.

By using an approximate value of –\(\sqrt{53}\), the negative irrational number –\(\sqrt{53}\) is located on the number line as we can observe in the above image.

Question 12.
–\(\sqrt{80}\)
Answer:
The –\(\sqrt{80}\) is between two integers. The two integers are -8 and -9.
By using calculator –\(\sqrt{80}\) = -8.944271909….
The value of –\(\sqrt{80}\) with two decimal places is -8.94.
The decimal -8.94 is closer to -8.9 than to -9.0.
So, –\(\sqrt{80}\) is located closer to -8.9.

By using an approximate value of –\(\sqrt{80}\), the negative irrational number –\(\sqrt{80}\) is located on the number line as we can observe in the above image.

Use a calculator. Locate each irrational number to 3 decimal places on the number line using rational approximations.

Question 13.
\(\sqrt{47}\)
Answer:
By using calculator \(\sqrt{47}\) = 6.855654600….
The value of \(\sqrt{47}\) with three decimal places is 6.855.
The decimal 6.855 is closer to 6.86 than to 6.85.
So, \(\sqrt{47}\) is located closer to 6.86.

The given irrational number \(\sqrt{47}\) is located on the number line by using rational approximation as we can observe in the above image.

Question 14.
–\(\sqrt{15}\)
Answer:
By using calculator –\(\sqrt{15}\) = –3.872983346….
The value of –\(\sqrt{15}\) with three decimal places is –3.872.
The decimal -3.872 is closer to –3.87 than to –3.88.
So, –\(\sqrt{15}\) is located closer to -3.87.

The given irrational number –\(\sqrt{15}\) is located on the number line by using rational approximation as we can observe in the above image.

Question 15.

Answer:
By using calculator = 4.54683594….
The value of with three decimal places is 4.546.
The decimal 4.546 is in between 4.5 and 4.6.
So, is located on 4.55.

The given irrational number is located on the number line by using rational approximation as we can observe in the above image.

Locate each irrational number on the number line using rational approximations.

Question 16.
\(\sqrt{101}\)
Answer:
By using calculator \(\sqrt{101}\) = 10.049875….
The value of \(\sqrt{101}\) with two decimal places is 10.04.
The decimal 10.04 is closer to 10 than to 10.1.
So, \(\sqrt{101}\) is located closer to 10.

The given irrational number \(\sqrt{101}\) is located on the number line by using rational approximation as we can observe in the above image.

Question 17.
–\(\sqrt{132}\)
Answer:
By using calculator –\(\sqrt{132}\) = – 11.489125….
The value of –\(\sqrt{132}\) with two decimal places is –11.48.
The decimal -11.48 is closer to –11.5 than to –11.4.
So, –\(\sqrt{132}\) is located closer to –11.5.

The given irrational number –\(\sqrt{132}\) is located on the number line by using rational approximation as we can observe in the above image.

Question 18.
\(\sqrt{2,255}\)
Answer:
By using calculator \(\sqrt{2,255}\) = 47.4868….
The value of \(\sqrt{2,2551}\) with two decimal places is 47.48.
The decimal 47.48 is closer to 47.5 than to 47.4.
So, \(\sqrt{2,255}\) is located closer to 47.5.

The given irrational number \(\sqrt{2,255}\) is located on the number line by using rational approximation as we can observe in the above image.

Solve.

Question 19.
Locate the value of the constant, π, on the number line using rational numbers.
Answer:
We know that π = 3.14159265

In the above image we can observe the value of the constant, π, is located on the number line using rational numbers.

Question 20.
3.1416 and \(\frac{22}{7}\) are two rational approximate values of π.

a) Graph 3.1416, \(\frac{22}{7}\), and π on the number line.
b) Which of the two rational approximate values is closer to π?
Answer:
a)We know that 22/7 = 3.1428, π = 3.14159

In the above image we can observe 3.1416, 22/7 and π on the number line.
b) The two rational approximate values closer to π are  3.1416 and 22/7.

Question 21.
A triangle is cut from a square as shown in the diagram. The area of the square is 59 square inches. Approximate the height of the triangle to 3 decimal places.

Answer:

Question 22.
Math Journal When do you need to approximate an irrational number with a rational value? Explain and illustrate with an example.
Answer:

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.2 Writing Rational Numbers as Decimals to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.2 Answer Key Writing Rational Numbers as Decimals

Math in Focus Grade 7 Chapter 1 Lesson 1.2 Guided Practice Answer Key

Using long division, write each rational number as a terminating decimal.

Question 1.
\(\frac{7}{8}\)
Answer:
7/8

Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. By using long division divide 7 by 8 the quotient is 0.875 which is a terminating decimal.

Question 2.
\(\frac{19}{4}\)
Answer:

Explanation:
Perform division operation on given rational number. By using long division divide 19 by 4 the quotient is 4.75 which is a terminating decimal.

Question 3.
\(\frac{52}{40}\)
Answer:

Explanation:
Perform division operation on given rational number. By using long division divide 52 by 40 the quotient is 1.3 which is a terminating decimal.

Question 4.
10\(\frac{13}{25}\)
Answer:
10(13/25)
= (250 + 13)/25
= 263/25

Explanation:
Perform division operation on given rational number. The mixed fraction 10(13/25) in fraction form as 263/25. By using long division divide 263 by 25 the quotient is 10.52 which is a terminating decimal.

Using long division, write each rational number as a repeating decimal.

Question 5.
\(\frac{2}{9}\)
Answer:

A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero. Perform division operation on given rational number. By using long division divide 2 by 9 the quotient is 0.222… which is a repeating decimal.

Question 6.
\(\frac{11}{6}\)
Answer:

Explanation:
A repeating decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero. Perform division operation on given rational number. By using long division divide 11 by 6 the quotient is 1.8333… which is a repeating decimal.

Using a calculator, write each rational number as a repeating decimal.

Question 7.
\(\frac{23}{24}\)
Answer:
23/24
= 0.958333…
Explanation:
Perform division operation on given rational number. By using calculator divide 23 by 24 the quotient is 0.958333… which is a repeating decimal.

Question 8.
\(\frac{78}{37}\)
Answer:
78/37
= 2.108108….
Explanation:
Perform division operation on given rational number. By using calculator divide 78 by 37 the quotient is 2.108108… which is a repeating decimal.

Using long division, write each rational number as a repeating decimal. Use bar notation to indicate the repeating digits.

Question 9.
\(\frac{5}{6}\)
Answer:

Explanation:
Perform division operation on given rational number. By using long division divide 5 by 6 the quotient is 0.8333… which is a repeating decimal. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above  image.

Question 10.
\(\frac{17}{12}\)
Answer:

Explanation:
Perform division operation on given rational number. By using long division divide 17 by 12 the quotient is 1.41666… which is a repeating decimal. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above  image.

Technology Activity

Materials:

• spreadsheet software

Classify rational numbers in decimal form

Work in pairs.

Step 1.
On a spreadsheet, label four columns with the following column heads.

Step 2.
Enter each rational number below in the first column, labeled “Rational Numbers in Decimal Form”. Make sure that the cells in this column are formatted to display decimals up to 8 decimal places.
\(\frac{5}{16}\), \(\frac{141}{25}\), –\(\frac{40}{111}\), –\(\frac{15}{16}\), \(\frac{14}{5}\), \(\frac{1}{8}\), –\(\frac{9}{44}\), \(\frac{2}{11}\), \(\frac{5}{4}\) and –\(\frac{40}{9}\).
For example, if you enter into the spreadsheet, the entry will show the decimal form of this fraction.

Step 3.
Determine whether the decimal ¡s terminating, repeating, or neither. Enter either “Terminating”, “Repeating”, or “Neither” in the second column.

Step 4.
If the decimal terminates, record the number of decimal digits in the third column. If the decimal repeats, record the repeating digits in the fourth column.
Example:

Math Journal
Did you find any decimals that neither terminated nor repeated? What can you conclude about the decimal form of a rational number?

Compare the positive rational numbers using the symbols < or >. Use a number line to help you.

Question 11.
\(\frac{7}{10}\) ? \(\frac{13}{16}\)
Answer:
7/10 < 13/16

Explanation:
In the above number line we can observe the given positive rational numbers. The positive rational number 7/10 is less than 13/16.

Question 12.
\(\frac{24}{7}\) ? \(\frac{10}{3}\)
Answer:
24/7 > 10/3

Explanation:
In the above number line we can observe the given positive rational numbers 24/7 and 10/3. The positive rational number 24/7 is greater than 10/3.

Compare the negative rational numbers using the symbols < or >. Use a number line to help you.

Question 13.
–\(\frac{3}{5}\) ? –\(\frac{4}{5}\)
Answer:
-3/5  > -4/5

Explanation:
In the above number line we can observe the given negative rational numbers -3/5 and -4/5. The negative rational number -3/5 is greater than -4/5.

Question 14.
-10\(\frac{3}{4}\) ? –\(\frac{41}{5}\)
Answer:
-10(3/4)
= -(40 + 3)/4
= -43/4
-10(3/4) < – 41/5

Explanation:
In the above number line we can observe the given negative rational numbers -10(3/4) and -41/5. The negative rational number -10(3/4) is less than -41/5.

Question 15.
-4.063 ? -4\(\frac{1}{6}\)
Answer:
-4(1/6)
= – (24 + 1)/6
= -25/6
-4.063 > -4(1/6)

In the above number line we can observe the given negative rational numbers -4.063 and -4(1/6). The negative rational number -4.063 is greater than -4(1/6).

Math in Focus Course 2A Practice 1.2 Answer Key

Using long division, write each rational number as a terminating decimal.

Question 1.
76\(\frac{1}{2}\)
Answer:
76(1/2)
= 153/2

Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. The mixed fraction 76(1/2) in fraction form is 153/2. By using long division divide 153 by 2 the quotient is 76.5 which is a terminating decimal.

Question 2.
-39\(\frac{2}{5}\)
Answer:
-39(2/5)
= -(195 + 2)/5
= -197/5

Explanation:
Perform division operation on given rational number. The mixed fraction -39(2/5) in fraction form is -197/5. By using long division divide -197 by 5 the quotient is -39.4 which is a terminating decimal.

Question 3.
–\(\frac{47}{10}\)
Answer:
-47/10

Explanation:
Perform division operation on given rational number. By using long division divide -47 by 10 the quotient is -4.7 which is a terminating decimal.

Question 4.
\(\frac{5}{16}\)
Answer:
5/16

Explanation:
Perform division operation on given rational number. By using long division divide 5 by 16 the quotient is 0.3125 which is a terminating decimal.

Question 5.
\(\frac{7}{20}\)
Answer:
7/20

Explanation:
Perform division operation on given rational number. By using long division divide 7 by 20 the quotient is 0.35 which is a terminating decimal.

Question 6.
\(\frac{7}{8}\)
Answer:
7/8

Explanation:
Perform division operation on given rational number. By using long division divide 7 by 8 the quotient is 0.875 which is a terminating decimal.

Simplify each rational number. Then use long division to write each rational number as a terminating decimal.

Question 7.
\(\frac{99}{36}\)
Answer:
99/36
= 11/4

Explanation:
The given ration number is 99/36. The simplified form of a given rational number is 11/4. Perform division operation on simplified rational number. By using long division divide 11 by 4 the quotient is 2.75 which is a terminating decimal.

Question 8.
\(\frac{12}{15}\)
Answer:
12/15
= 4/5

Explanation:
The given ration number is 12/15. The simplified form of a given rational number is 4/5. Perform division operation on simplified rational number. By using long division divide 4 by 5 the quotient is 0.8 which is a terminating decimal.

Question 9.
\(\frac{9}{48}\)
Answer:
9/48
= 3/16

Explanation:
The given ration number is 9/48. The simplified form of a given rational number is 3/16. Perform division operation on simplified rational number. By using long division divide 3 by 16 the quotient is 0.1875 which is a terminating decimal.

Question 10.
–\(\frac{132}{8}\)
Answer:
-132/8
= -33/2

Explanation:
The given ration number is -132/8. The simplified form of a given rational number is -33/2. Perform division operation on simplified rational number. By using long division divide -33 by 2 the quotient is -16.5 which is a terminating decimal.

Question 11.
–\(\frac{48}{50}\)
Answer:
-48/50
= -24/25

Explanation:
The given ration number is -48/50. The simplified form of a given rational number is -24/25. Perform division operation on simplified rational number. By using long division divide -24 by 25 the quotient is -0.96 which is a terminating decimal.

Question 12.
–\(\frac{14}{128}\)
Answer:
-14/128
= -7/64

Explanation:
The given ration number is -14/128. The simplified form of a given rational number is -7/64. Perform division operation on simplified rational number. By using long division divide -7 by 64 the quotient is -0.109375 which is a terminating decimal.

Using long division, write each rational number as a repeating decimal with 3 decimal places. Identify the pattern of repeating digits using bar notation.

Question 13.
\(\frac{5}{6}\)
Answer:

Explanation:
Perform division operation on given rational number. By using long division divide 5 by 6 the quotient is 0.83333… which is a repeating decimal. The repeating decimal with 3 decimal places is denoted as 0.833 bar for the number 3 on last. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above  image.

Question 14.
-8\(\frac{2}{3}\)
Answer:
-8(2/3)
= -(24+2)/3
= -26/3

Explanation:
The mixed fraction -8(2/3) in fraction form is -26/3. Perform division operation on fraction. By using long division divide -26 by 3 the quotient is -8.66666… which is a repeating decimal. The repeating decimal with 3 decimal places is denoted as -8.666 bar for the number 6 on last. The repeating digits are denoted by this ¯¯¯ symbol as we can observe in the above  image.

Write each rational number as a repeating decimal using bar notation. You may use a calculator.

Question 15.
\(\frac{8}{55}\)
Answer:
8/55
= 0.1454545…
=
Explanation:
Perform division operation on given rational number. By using calculator divide 8 by 55 the quotient is 0.1454545… which is a repeating decimal. The repeating decimal 45 is represented by bar notation as we can observe in the answer.

Question 16.
\(\frac{456}{123}\)
Answer:
456/123
= 3.7073170731….
=
Explanation:
Perform division operation on given rational number. By using calculator divide 456 by 123 the quotient is 3.7073170731… which is a repeating decimal. The repeating decimal 70731 is represented by bar notation as we can observe in the answer.

Question 17.
–\(\frac{987}{110}\)
Answer:
-987/110
= -8.9727272….
=
Explanation:
Perform division operation on given rational number. By using calculator divide -987 by 110 the quotient is -8.9727272… which is a repeating decimal. The repeating decimal 72 is represented by bar notation as we can observe in the answer.

Question 18.
\(\frac{11}{14}\)
Answer:
11/14
= 0. 7857142857142….
=

Explanation:
Perform division operation on given rational number. By using calculator divide 11 by 14 the quotient is 0.7857142857142… which is a repeating decimal. The repeating decimal 857142 is represented by bar notation as we can observe in the answer.

Question 19.
–\(\frac{10}{13}\)
Answer:
-10/ 13
= – 0. 769230769230….
=

Explanation:
Perform division operation on given rational number. By using calculator divide -10 by 13 the quotient is -0.769230769230… which is a repeating decimal. The repeating decimal 769230 is represented by bar notation as we can observe in the answer.

Question 20.
\(\frac{4,005}{101}\)
Answer:
4,005/101
= 39.65346534….
=

Explanation:
Perform division operation on given rational number. By using calculator divide 4,005 by 101 the quotient is 39.65346534… which is a repeating decimal. The repeating decimal 6534 is represented by bar notation as we can observe in the answer.

Refer to the list of rational numbers below for questions 21 to 23, You may use a calculator.

–\(\frac{23}{32}\), \(\frac{7}{15}\), –\(\frac{368}{501}\), –\(\frac{19}{26}\), \(\frac{37}{44}\)

Question 21.
Write each rational number as a decimal with at most 6 decimal places.
Answer:
Given rational numbers are -23/32, 7/15, -368/501, -19/26, 37/44.
The given rational numbers in a decimal form with at most 6 decimal places.
-0.71875, 0.466667, -0.734531, -0.730769, 0.840909

Question 22.
Using your answers in 21 list the numbers from least to greatest using the symbol <. Graph a number line between —1 and 1 with 0 in the middle. Then, place each rational number on the number line.
Answer:

Explanation:
From the answer 21 the numbers from least to greatest are -368/501, -19/26, -23/32, 7/15, 37/44. In the above image we can observe the above given rational numbers on the number line.

Question 23.
Math Journal Margo tries to compare –\(\frac{2}{3}\) and –\(\frac{5}{8}\) using absolute values. She finds their decimal equivalents to be –\(0 . \overline{6}\) and —0.625, and she knows |-\(0 . \overline{6}\)| |-0.625|. Explain why she must reverse the inequality in her final answer, –\(\frac{2}{3}\) < –\(\frac{5}{8}\)
Answer:
The greater the absolute value of a number the farther that number is from 0.
So, -2/3 is farther to the left of 0 than -5/8.
A number that is to the left of another number on the number line is less than that number. So, -2/3 < -5/8.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.1 Representing Rational Numbers on the Number Line to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.1 Answer Key Representing Rational Numbers on the Number Line

Math in Focus Grade 7 Chapter 1 Lesson 1.1 Guided Practice Answer Key

Solve.

Question 1.
Find the absolute values of 3\(\frac{2}{7}\) and –\(\frac{18}{5}\)
Answer:
3(2/7) = (21+2)/7 = 23/7
The simplified form of 3(2/7) is 23/7
The absolute value of |3(2/7)| is 3(2/7)
The absolute value of |-(18/5)| is 18/5

Question 2.
Graph the two numbers on a number line and indicate their distances from 0. Which number is farther from 0?
Answer:

The number -18/5 is farther from 0.
Explanation:
In the above image we can observe a number line. On the number line the two numbers 3(2/7) and -18/5 are indicated. The two numbers distance from 0 are graphed. The number -18/5 is farther from 0.

Write each number in \(\frac{m}{n}\) form where m and n are integers.

Question 3.
11\(\frac{1}{6}\)
Answer:
11(1/6)
= (66 + 1)/6
= 67/6
The number 11(1/6) in m/n form is 67/6.
Here m = 67 and n= 6

Question 4.
48
Answer:
48 = 48/1
The number 48 in m/n form is 48/1.
Here m = 48 and n = 1

Question 5.
-5\(\frac{4}{12}\)
Answer:
-5(4/12)
= – (60 + 4)/12
= -64/12
= -16/3
The number -5(4/12) in m/n form is -16/3.
Here m = -16 and n = 3

Question 6.
–\(\frac{25}{10}\)
Answer:
-25/10 = -5/2
The given number -25/10 is already in m/n form.

Write each decimal as \(\frac{m}{n}\) where m and n are integers with n ≠ 0.

Question 7.
11.5
Answer:
11.5 = 23/2
The given decimal number 11.5 is represented in m/n form. The m/n form of 11.5 is 23/2.

Question 8.
-7.8
Answer:
-7.8 = -78/10
The given decimal number -7.8 is represented in m/n form. The m/n form of -7.8 is -78/10.

Question 9.
0.36
Answer:
0.36 = 36/100
The given decimal number 0.36 is represented in m/n form. The m/n form of 0.36 is 36/100.

Question 10.
-0.125
Answer:
-0.125 = – 125/1000
The given decimal number -0.125 is represented in m/n form. The m/n form of -0.125 is 125/1000.

Copy and complete.

Question 11.
Locate the rational numbers -1.5 and \(\frac{15}{4}\) on the number line.
STEP 1
Find the integers that the rational number lies between.
\(\frac{15}{4}\) can be written as a mixed number, 3\(\frac{3}{4}\), and 3\(\frac{3}{4}\) lies between 3 and 4. The negative decimal -1.5 lies between —2 and —1.
STEP 2
Graph a number line and label the integers.

Answer:

The integers are labeled on a number line.
STEP 3
Divide the distance between the integers into equal segments.
You divide the distance between —2 and —1 into segments and the distance between 3 and 4 into segments.

Answer:

Divide the distance between —2 and —1 into 1 segments and the distance between 3 and 4 into 3 segments.
STEP4
Use the segments to locate -1.5 and 3\(\frac{3}{4}\).

Answer:

Located the rational numbers -1.5 and 15/4 on the number line.

Locate the following rational numbers on the number line.

Question 12.
\(\frac{1}{6}\) and \(\frac{15}{3}\)
Answer:
1/6 and 15/3

Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The fraction 1/6 lies between 0 and 1. The simplified form of 15/3 is 5. The fraction 15/3 lies on number 5.
Next we have to label the integers and locate the rational numbers on a number line.
In the above image we can observe the rational numbers 1/6 and 15/3 are located on the number line.

Question 13.
-0.4 and \(\frac{11}{5}\)
Answer:
-0.4 and 11/5

Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative decimal -0.4 lies between —1 and 0.The fraction 11/5 lies between 2 and 3.
Next we have to label the integers and locate the rational numbers on a number line.
Divide the distance between —1 and 0 into 4 segments and the distance between 2 and 3 into 4 segments.
In the above image we can observe the rational numbers -0.4 and 11/5 are located on the number line.

Question 14.
\(\frac{12}{15}\) and -1.8
Answer:
12/15 and -1.8

Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative decimal -1.8 lies between —2 and -1.The fraction 12/15 lies between 0 and 1.
Next we have to label the integers and locate the rational numbers on a number line.
Divide the distance between —2 and -1 into 4 segments and the distance between 0 and 1 into 4 segments.
In the above image we can observe the rational numbers -1.8 and 12/15 are located on the number line.

Question 15.
\(-\frac{5}{15}\) and \(-\frac{25}{30}\)
Answer:
-5/15 and 25/30

Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative fractions -25/30 and -5/15 lies between —1 and 0.
Next we have to label the integers and locate the rational numbers on a number line.
In the above image we can observe the rational numbers -25/30 and -5/15 are located on the number line.

Math in Focus Course 2A Practice 1.1 Answer Key

Find the absolute value of each fraction. Use a number line to show how far the fraction is from 0. Write fractions in simplest form.

Question 1.
\(\frac{7}{10}\)
Answer:
7/10

The absolute value of above fraction is 7/10.
Explanation:
First we have to find where the fraction lies between on the number line.
The fraction 7/10 lies between 0 and 1.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is 7/10 units far from the 0 on the number line.

Question 2.
\(\frac{18}{8}\)
Answer:
The absolute value of 18/8 is 18/8.
18/8 = 9/4
The simplest form of 18/8 is 9/4.

Explanation:
First we have to find where the fraction lies between on the number line.
The fraction 18/8 lies between 2 and 3.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is 18/8 units far from the 0 on the number line.

Question 3.
–\(\frac{5}{13}\)
Answer:
The absolute value of -5/13 is 5/13.

Explanation:
First we have to find where the fraction lies between on the number line.
The fraction -5/13 lies between -1 and 0.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is -5/13 units far from the 0 on the number line.

Question 4.
–\(\frac{48}{15}\)
Answer:
-48/15
The absolute value of -48/15 is 48/15.

Explanation:
First we have to find where the fraction lies between on the number line.
The fraction -48/15 lies between -3 and 0.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is -48/15 units far from the 0 on the number line.

Write each integer or fraction as \(\frac{m}{n}\) in simplest form where m and n are integers.

Question 5.
67
Answer:
67
= 67/1
The number 67 in m/n form is 67/1.
Here m = 67 and n= 1

Question 6.
-345
Answer:
-345
= -345/1
The number -345 in m/n form is -345/1.
Here m = -345 and n= 1

Question 7.
\(\frac{25}{80}\)
Answer:
25/80
= 5/16
The simplest form of 25/80 is 5/16.
The fraction 25/80 in m/n form is 5/16.
Here m = 5 and n= 16

Question 8.
–\(\frac{264}{90}\)
Answer:
-264/90
= -44/15
The simplest form of -264/90 is -44/15.
The fraction -264/90 in m/n form is -44/15.
Here m = -44 and n= 15

Question 9.
–\(\frac{14}{70}\)
Answer:
-14/70
= -1/5
The simplest form of -14/70 is -1/5.
The fraction -14/70 in m/n form is -1/5.
Here m = -1 and n= 5

Question 10.
\(\frac{600}{480}\)
Answer:
600/480
= 50/40
= 5/4
The simplest form of 600/480 is 5/4.
The fraction 600/480 in m/n form is 5/4.
Here m =5 and n = 4

Write each mixed number or decimal \(\frac{m}{n}\) as in simplest form where m and n are integers.

Question 11.
7\(\frac{7}{9}\)
Answer:
7(7/9)
= (63 + 7)/9
= 70/9
The simplest form of the mixed number 7(7/9) is 70/9.
Here m = 70 and n = 9 both are integers.

Question 12.
-5\(\frac{1}{10}\)
Answer:
-5(1/10)
= -(50 + 1)/10
= -51/10
The simplest form of the mixed number -5(1/10) is -51/10.
Here m = -51 and n = 10 both are integers.

Question 13.
2\(\frac{5}{12}\)
Answer:
2(5/12)
= (24 + 5)/12
= 29/12
The simplest form of the mixed number 2(5/12) is 29/12.
Here m = 29 and n = 12 both are integers.

Question 14.
-10\(\frac{11}{36}\)
Answer:
-10(11/36)
=-(360 + 11)/36
= -371/36
The simplest form of the mixed number-10(11/36) is -371/36.
Here m =-371 and n = 36 both are integers.

Question 15.
0.4
Answer:
0.4
= 4/10
= 2/5
The simplest form of the decimal number 0.4 is 2/5.
Here m = 2 and n = 5 both are integers.

Question 16.
-0.625
Answer:
-0.625
= -625/1000
= -5/8
The simplest form of the decimal number -0.625 is -5/8.
Here m = -5 and n = 8 both are integers.

Question 17.
5.80
Answer:
5.80
= 29/5
The simplest form of the decimal number 5.80 is 29/5.
Here m = 29 and n = 5 both are integers.

Question 18.
9.001
Answer:
9.001
= 9001/1000
The simplest form of the decimal number 9.001 is 9001/1000.
Here m = 9001 and n =1000 both are integers.

Question 19.
-10.68
Answer:
-10.68
= -267/25
The simplest form of the decimal number -10.68 is -267/25.
Here m = -267 and n = 25 both are integers.

Copy and complete.

Question 20.
Locate the following rational numbers correctly on the number line.
–\(\frac{1}{4}\), -1.5, 0.8, \(\frac{5}{2}\)

Answer:

Explanation:
First we have to find where the given rational numbers lies between on the number line.
The negative decimal -1.5 lies between -2 and -1.
The negative fraction -1/4 lies between -1 and 0.
The decimal 0.8 lies between 0 and 1.
The fraction 5/2 lies between 2 and 3.
The above given rational numbers are located correctly on the number line.

Question 21.
Locate the following rational numbers correctly on the number line.
1\(\frac{7}{10}\), –\(\frac{13}{5}\), 2.25, -0.7

Answer:

Explanation:
First we have to find where the given rational numbers lies between on the number line.
The negative fraction -13/5 lies between -3 and -2
The negative decimal -0.7 lies between -1 and 0.
The mixed fraction 1(7/10) in fraction as 17/10 lies between 1 and 2.
The decimal 2.25 lies between 2 and 3.
The above given rational numbers are located correctly on the number line.

Graph each rational number on a separate number line.

Question 22.
67\(\frac{1}{8}\)
Answer:
67(1/8)
= (536 + 1)/8
= 537/8

Explanation:
First we have to find where the given rational number lies between on the number line.
The mixed fraction 67(1/8) in fraction as 537/8 lies between 67 and 68.
The above given rational number is drawn correctly on the number line.

Question 23.
\(\frac{305}{20}\)
Answer:
305/20

Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction 305/20 lies between 15 and 16.
The above given rational number is drawn correctly on the number line.

Question 24.
\(\frac{98}{28}\)
Answer:
98/28

Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction 98/28 lies between 3 and 4.
The above given rational number is drawn correctly on the number line.

Question 25.
–\(\frac{21}{12}\)
Answer:
-21/12

Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction -21/12 lies between -2 and -1.
The above given rational number is correctly drawn on the number line.

Question 26.
-25.8
Answer:

Explanation:
First we have to find where the given rational number lies between on the number line.
The decimal lies between -26 and -25.
The above given rational number is  drawn correctly on the number line.

Question 27.
-45.3
Answer:

Explanation:
First we have to find where the given rational number lies between on the number line.
The decimal lies between -46 and -45.
The above given rational number is correctly drawn on the number line.

A video game gives you 10 minutes to find a treasure. The results of your first 8 games show the amount of time left unused when you have found the treasure. A negative time means you have gone beyond the 10 minutes allotted. Use these data for questions 28 to 35.

\(\frac{23}{8}\), 0, -7\(\frac{1}{5}\), 6, –\(\frac{17}{4}\), 8, 7.8, -9.1

Question 28.
Order the times left from most to least time using the symbol >.
Answer:
The time left from most to least are 8, 7.8, 6, 23/8, 0, -17/4, -7(1/5), -9.1.

Question 29.
Write the absolute value of each number.
Answer:
23/8, 0, -7(1/5), 6 , -17/4, 8, 7.8, -9.1
The absolute value of 23/8 is 23/8.
The absolute value of 0 is 0.
The absolute value of -7(1/5) is 7(1/5) or 36/5.
The absolute value of 6 is 6.
The absolute value of -17/4 is 17/4.
The absolute value of 8 is 8.
The absolute value of 7.8 is 7.8.
The absolute value of -9.1 is 9.1.

Question 30.
Which number has the greatest absolute value?
Answer:
The decimal number – 9.1 has the greatest absolute value.

Question 31.
Order the absolute values from least to greatest. Use the symbol <.
Answer:
The absolute values from least to greatest are 0 < 23/8 < 17/4 < 6 < 7(1/5) < 7.8 < 8 < 9.1.

Question 32.
Graph the original numbers on a number line.
Answer:
23/8, 0, -7(1/5), 6 , -17/4, 8, 7.8, -9.1

The original numbers on a number line is drawn on the graph.

Question 33.
Which negative number in the list is farthest from 0?
Answer:
The negative number –9.1 in the given list is farthest from 0.

Question 34.
Which positive number in the list is closest to 10?
Answer:
The positive number 8 in the given list is closest to 10.

Question 35.
Which time is closest to —5 minutes?
Answer:
The time -17/4 is closest to – 5 minutes.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 The Real Number System to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Answer Key The Real Number System

Math in Focus Grade 7 Chapter 1 Quick Check Answer Key

Order the numbers from least to greatest. Use the < symbol. Graph each number on a horizontal number line.

Question 1.
\(\frac{11}{17}\), 1\(\frac{3}{5}\), 0.3, 1.6, \(\frac{19}{10}\)
Answer:
\(\frac{11}{17}\), 1\(\frac{3}{5}\), 0.3, 1.6, \(\frac{19}{10}\)
The given numbers from least to greatest are 0.3 < \(\frac{11}{17}\) < 1\(\frac{3}{5}\)  or 1.6 < 19/10.

In the above image we can observe the given numbers on a horizontal number line.

Compare. Copy and complete each ? with <, > or =

Question 2.
3.87 ? 3.68
Answer:
3.87 > 3.68
Explanation:
Compare the above given two decimal numbers. The two decimal numbers are 3.87 and 3.68. The decimal number 3.87 is greater than 3.68.

Question 3.
0.982 ? 0.982
Answer:
0.982 = 0.982
Explanation:
Compare the above given two decimal numbers. The two decimal numbers are 0.982 and 0.982. The decimal number 0.982 is equal to 0.982.

Question 4.
5.23 ? 5.235
Answer:
5.23 < 5.235
Explanation:
Compare the above given two decimal numbers. The two decimal numbers are 5.23 and 5.235. The decimal number 5.23 is less than 5.235.

Round each number.

Question 5.
1,456 to the nearest hundred.
Answer:
Explanation:
1,456 is rounded to the nearest hundred as 1,500.
Explanation:
The number 1,456 is between 1,400 and 1,500. 1,450 is the midpoint between 1,400 and 1,500. The number 1,456 is greater than the midpoint. So, 1,456 is rounded to the nearest hundred as 1,500

Question 6.
849.58 to the nearest whole number.
Answer:
849.58 is rounded to the nearest whole number as 850.
Explanation:
Here, the tenths value is 5 which is greater than or equal to 5, increase the whole number ones place by 1, and remove all the digits after the decimal point.
The number 849.58 becomes 850 after rounding to the nearest whole number.

Question 7.
4,923 to the nearest ten.
Answer:
4923 is rounded to the nearest ten is 4920
When we are rounding to the nearest ten, we have to follow the below rules.
We have to round the number up. If the last digit in the number is 5, 6, 7, 8, or 9.
We have to round the number down. If the last digit in the number is 1, 2, 3, or 4.

Question 8.
23.84 to 1 decimal place.
Answer:
23.84 is rounded to 1 decimal place is 23.8.
Explanation:
If the last digit in 23.84 is less than 5, then remove the last digit.
If the last digit in 23.84 is 5 or more and the second to the last digit in 23.84 is less than 9, then remove the last digit and add 1 to the second to the last digit.
If the last digit in 23.84 is 5 or more and the second to the last digit in 23.84 is 9, then remove the last digit, make the second to last digit 0, and add 1 to the number to the left of the decimal place.
The last digit in 23.84 is less than 5, So we have to remove the last digit. 23.84 is rounded to 23.8.

Question 9.
306.128 to the nearest hundredth.
Answer:
306.128 is rounded to the nearest hundredth is 306.13.
Explanation:
If the digit after hundredth is greater than or equal to 5, then add 1 to hundredth. Else remove the digit.
The third digit of 306.128 right of decimal point is 8. Add 1 to the before decimal number then the number is 306.13.

Round 9,909.937 as indicated.

Question 10.
To 2 decimal places
Answer:
9,909.937 is rounded to 2 decimal place is 9,909.9.
Explanation:
If the last digit after decimal point is greater than or equal to 5, then add 1 to before decimal number. Else remove the digit.
9,909.937 the third digit of right of decimal point is 7. Add 1 to the before decimal number then the number is 9,909.94
The second digit after decimal point is 4 which is less than 5.
So remove the number 4, the result is 9,909.9.

Question 11.
To the nearest whole number
Answer:
9,909.937 is rounded to nearest whole number is 9,910.
Explanation:
Here, the hundredths value is 9 which is greater than 5. Increase the whole number ones place by 1, and remove all the digits after the decimal point.
9,909.937 after rounding to the nearest whole number becomes 9,910.

Question 12.
To the nearest whole number
Answer:
9,909.937 is rounded to nearest whole number is 9,910.
Explanation:
Here, the hundredths value is 9 which is greater than 5. Increase the whole number ones place by 1, and remove all the digits after the decimal point.
9,909.937 after rounding to the nearest whole number becomes 9,910.

Question 13.
To the nearest ten
Answer:
9,909.937 is rounded to nearest ten is 9,909.9.
Explanation:
If the digit after tenth is greater than or equal to 5, add 1 to tenth. Else remove the digit.
The third digit after decimal point is 7 which is greater than 5. Add 1 to the 3 which is second digit of the given number is 9,909.94.
The second digit after decimal point is 4 which is less than 5. So, remove the digits after 9.
The Result is equal to 9,909.9

Find the square of each number.

Question 14.
3
Answer:
3²
3 x 3 = 9
Explanation:
The given number is 3. Here we have to find the square of the given number. The square of number 3 is 9.

Question 15.
12
Answer:
12²
12 x 12 = 144
Explanation:
The given number is 12. Here we have to find the square of the given number. The square of number 12 is 144.

Find the cube of each number.

Question 16.
5
Answer:
5³
5 x 5 x 5 = 125
Explanation:
The given number is 5. Here we have to find the cube of the given number. The cube of number 5 is 125.

Question 17.
6
Answer:
6³
6 x 6 x 6 = 216
Explanation:
The given number is 6. Here we have to find the cube of the given number. The cube of number 6 is 216.

Find the square root and cube root of each number.

Question 18.
64
Answer:
\(\sqrt{64}\) = 8
3 √64 = 4
Explanation:
The square root of 64 is equal to 8.
The cube root of 64 is equal to 4.

Question 19.
729
Answer:
\(\sqrt{729}\) = 27
3 √729 = 9
Explanation:
The square root of 729 is equal to 27.
The cube root of 729 is equal to 9.

Order the numbers from greatest to least. Use the > symbol.

Question 20.
\(\sqrt{81}\), 8², 3³
Answer:
\(\sqrt{81}\) = 9
8² = 64
3³  = 27
The numbers from greatest to least are 8², 3³ ,\(\sqrt{81}\).

Use the following set of numbers for questions 21 to 25.

34, -23, -54, 54, -60

Question 21.
Find the absolute value of each number.
Answer:
The absolute values of the given numbers are as below.
The absolute value of |34| is 34.
The absolute value of |-23| is 23.
The absolute value of |-54| is 54.
The absolute value of |54| is 54.
The absolute value of |-60| is 60.

Question 22.
Which number is closest to 0?
Answer:
The given set of numbers are 34, -23, -54, 54, -60
The number -23 is closest to 0.

Question 23.
Which number is farthest from 0?
Answer:
The given set of numbers are 34, -23, -54, 54, -60.
The number -60 is farthest from 0.

Question 24.
Name two numbers with the same absolute value.
Answer:
The given set of numbers are 34, -23, -54, 54, -60.
The absolute value of |-54| is 54.
The absolute value of |54| is 54.
The two numbers with the same absolute values are  -54 and 54.

Question 25.
Which number has the greatest absolute value?
Answer:
The given set of numbers are 34, -23, -54, 54, -60.
The absolute value of |-60| is 60.
The number -60 has the greatest absolute value  as we can observe in the answer 21.

Use the number line to find the absolute value of each of the following numbers.

Question 26.
|-15|
Answer:

The given number is |-15|.
The absolute value of the number |-15| is 15.
So the number |-15| is 15 units from 0.

Question 27.
|6|
Answer:

The given number is |6|.
The absolute value of the number |6| is 6.
So the number |6| is 6 units from 0.

Question 28.
|-2.1|
Answer:

The given number is |-2.1|.
The absolute value of the number |-2.1| is 2.1.
So the number |-2.1| is 2.1 units from 0.

Copy and complete each ? with >, =, or <.

Question 29.
|-7| ? |-72|
Answer:
|-7| < |-72|
Explanation:
The absolute value of |-7|  is 7.
The absolute value of |-72|  is 72.
So, |-7| is less than  |-72|.

Question 30.
|5| ? |-5|
Answer:
|5| = |-5|
Explanation:
The absolute value of |5| is 5.
The absolute value of |-5| is 5.
So, |5| is equal to |-5|.

Question 31.
|-26| ? |5|
Answer:
|-26| = |5|
Explanation:
The absolute value of |-26| is 26.
The absolute value of |5| is 5.
So, |-26| is greater than |5|.

Go through the Math in Focus Grade 1 Workbook Answer Key Chapter 16 Practice 2 Place Value to finish your assignments.

Math in Focus Grade 1 Chapter 16 Practice 2 Answer Key Place Value

Look at the pictures. Then fill in the blanks.

Example

Question 1.

Answer:
78 = 7 tens 8 ones.

Explanation:
In the above image, we can see that there are 7 tens and 8 ones which are 78.

Question 2.

Answer:
36 = 3 tens 6 ones.

Explanation:
In the above image, we can see that there are 3 tens and 6 ones which are 36.

Question 3.

Answer:
92 = 9 tens 2 ones.

Explanation:
In the above image, we can see that there are 9 tens and 2 ones which are 92.

Question 4.

Answer:
57 = 5 tens 7 ones.

Explanation:
In the above image, we can see that there are 5 tens and 7 ones which are 57.

Question 5.

Answer:
84 = 8 tens 4 ones.

Explanation:
In the above image, we can see that there are 8 tens and 4 ones which are 84.

Count the base-ten blocks. Then fill in the blanks.

Example

Question 6.

Answer:
93 = 9 tens 3 ones.
90 + 3 = 93.

Explanation:
In the above image, we can see that there are 9 tens and 3 ones which are 93.
90+3 = 93.

Question 7.

Answer:
87 = 8 tens 7 ones.
80+7 = 87.

Explanation:
In the above image, we can see that there are 8 tens and 7 ones which are 87.
80+7= 87.

Fill in the place-value charts.

Question 8.

Answer:
43 = 4 tens 3 ones.

Explanation:
Here, place value is a value represented by a digit in a number on the basis of its position in the number. So the place value of 43 is 4 in the tens place and 3 in ones place.

Question 9.

Answer:
86 = 8 tens and 6 ones.

Explanation:
Here, place value is a value represented by a digit in a number on the basis of its position in the number. So the place value of 86 is 8 in the tens place and 6 in ones place.

Question 10.

Answer:
64 = 6 tens 4 ones.

Explanation:
Here, place value is a value represented by a digit in a number on the basis of its position in the number. So the place value of 64 is 6 in the tens place and 4 in ones place.

Question 11.

Answer:
97 = 9 tens 7 ones.

Explanation:
Here, place value is a value represented by a digit in a number on the basis of its position in the number. So the place value of 97 is 9 in the tens place and 7 in ones place.

Question 12.

Answer:
75 = 7 tens 5 ones.

Explanation:
Here, place value is a value represented by a digit in a number on the basis of its position in the number. So the place value of 75 is 7 in the tens place and 5 in ones place.

Go through the Math in Focus Grade 1 Workbook Answer Key Chapter 16 Practice 1 Counting to 100 to finish your assignments.

Math in Focus Grade 1 Chapter 16 Practice 1 Answer Key Counting to 100

Count in tens and ones.

Fill in the blanks.

Example

Question 1.

Answer:
10,20,30,40,50,51,52.

Explanation:
In the above image, we can see that there are 5 tens and 2 ones which is 52.

Question 2.

Answer:
10,20,30,40,50,60,61,62,63.

Explanation:
In the above image, we can see that there are 6 tens and 3 ones which is 63.

Question 3.

Answer:
10,20,30,40,50,60,70,80,81,82,83,84.

Explanation:
In the above image, we can see that there are 8 tens and 4 ones which is 84.

Write the number.

Question 4.
forty-nine _____
Answer:
forty-nine – 45.

Explanation:
Given that forty-nine, so in numbers, it will be 45.

Question 5.
sixty-eight _____
Answer:
sixty-eight – 68.

Explanation:
Given that sixty-eight, so in numbers, it will be 68.

Question 6.
ninety-five _____
Answer:
ninety-five – 95.

Explanation:
Given that ninety-five, so in numbers, it will be 95.

Question 7.
eighty-seven _____
Answer:
eighty-seven – 87.

Explanation:
Given that eighty-seven, so in numbers, it will be 87.

Question 8.
fifty-six _____
Answer:
fifty-six – 56.

Explanation:
Given that fifty-six, so in numbers, it will be 56.

Question 9.
seventy-three _____
Answer:
seventy-three – 73.

Explanation:
Given that seventy-three, so in numbers, it will be 73.

Question 10.
ninety-two _____
Answer:
ninety-two – 92.

Explanation:
Given that ninety-two, so in numbers, it will be 92.

Match the number to the words.

Question 11.

Answer:

Find the missing numbers.

Question 12.
60 and 4 make _____
Answer:
60 and 4 make 64.

Explanation:
Given that 60 and 4 make 64.

Question 13.
5 and 70 make _____
Answer:
5 and 70 make 75.

Explanation:
Given that 5 and 70 make 75.

Question 14.
50 and ____ make 53.
Answer:
50 and 3 make 53.

Explanation:
Here, 53 makes 50 and 3.

Question 15.
____ and 4 make 84.
Answer:
80 and 4 make 84.

Explanation:
Here, 84 makes 80 and 4.

Question 16.
40 + 5 = ____
Answer:
40 + 5 = 45.

Explanation:
Given that 40+5 makes 45.

Question 17.
___ + 80 = 88
Answer:
8 + 80 = 88.

Explanation:
Here, 88 makes 8 + 80.

Circle a group of 10. Estimate how many there are. Then count.

Question 18.

Answer:
The actual count is 50 and the estimated is 55.

Explanation:
In the image, we can see 5 groups with 10 half-moons. So the estimation will be 55 and the count is 50.

Question 19.

Answer:
The actual count is 41 and the estimated is 41.

Explanation:
In the image, we can see 4 groups with 10 stars. So the estimation will be 40 and the count is 41.