Hillary

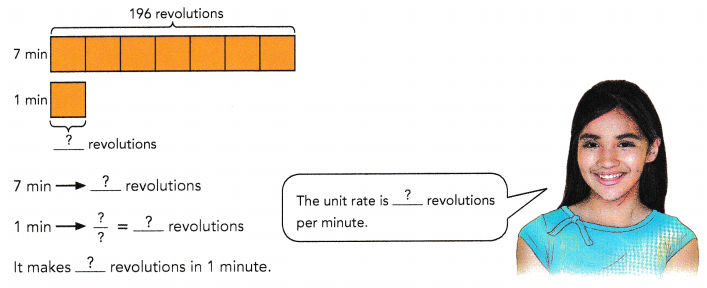
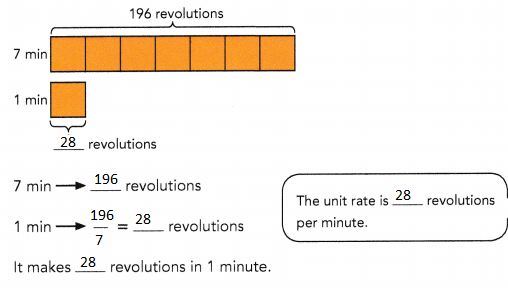
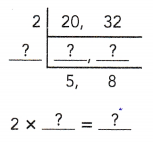Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 4 Lesson 4.2 Equivalent Ratios to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 4 Lesson 4.2 Answer Key Equivalent Ratios

Math in Focus Grade 6 Chapter 4 Lesson 4.2 Guided Practice Answer Key

Complete.

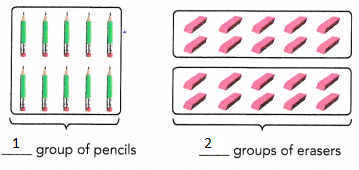
Question 1.

The ratio of the number of pencils to the number of erasers is : .
Answer:
1 : 2
Explanation:
The ratio of the number of pencils to the number of erasers is
10 : 20 = 1 : 2

Question 2.

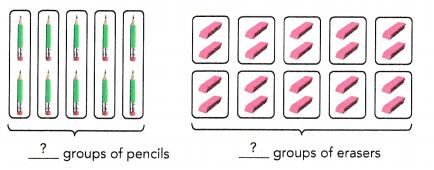
The ratio of the number of groups of pencils to the number of groups of erasers is : .
Answer:
1 : 2
Explanation:

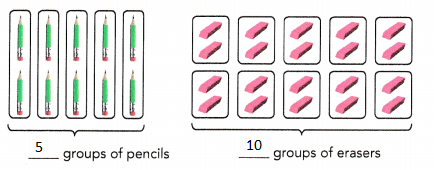
The ratio of the number of groups of pencils to the number of groups of erasers is
5 : 10 = 1 : 2

Question 3.

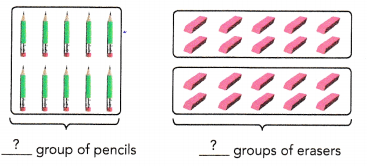
The ratio of the number of groups of pencils to the number of groups of erasers is : .
Answer:
1 : 2
Explanation:

The ratio of the number of groups of pencils to the number of groups of erasers is = 1 : 2

Question 4.

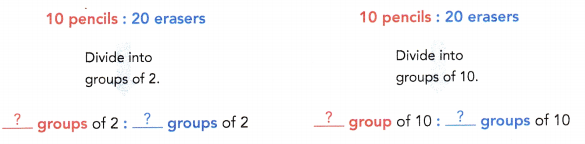
The ratio : , : , and : are equivalent ratios.
Answer:
1 : 2
Explanation:
The ratio 10 : 20, 5 : 10, and  1:2 are equivalent ratios.

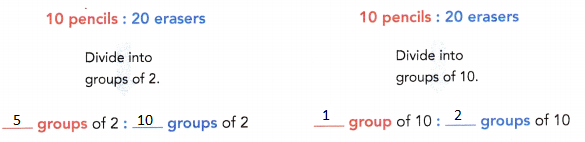
Question 5.
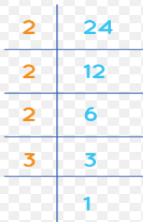
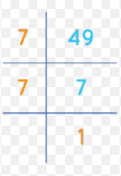
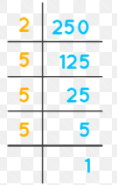
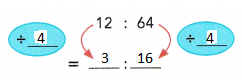
Express the ratio 12 : 64 in simplest form.

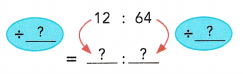
Answer:
3 : 16
Explanation:
the ratio 12 : 64 in simplest form.

Question 6.
Express the ratio 7 kg : 21 g in simplest form.
7 kg = g
7 kg : 21 g = g : g
= ÷ : ÷
= :
Answer:
1000 : 3
Explanation:
7 kg = 7000 g
7 kg : 21 g = 7000 g : 21 g
= 7000 ÷ 7 : 21 ÷ 7
= 1000 : 3

State whether each pair of ratios are equivalent.

Question 7.
7 : 8 and 8 : 7
Answer:
NO, pair of ratios are not equivalent.
Explanation:
7 : 8 and 8 : 7 are not equivalent

Question 8.
5 : 9 and 15 : 27
Answer:
YES, pair of ratios are equivalent
Explanation:
5 : 9 and 15 : 27
5 : 9 and 15 ÷ 3 : 27 ÷  3
5 : 9 and 5 : 9
5 : 9 and 15 : 27 are equivalent

Question 9.
12 : 13 and 24 : 39
Answer:
NO, pair of ratios are not equivalent.
Explanation:
12 : 13 and 24 : 39
For and 12, 24 common factor is 2,
where as 13 and 39 has common factor 13 .
12 : 13 and 24 : 39 are not equivalent ratios.

Question 10.
4 : 24 and 8 : 48
Answer:
YES, pair of ratios are equivalent.
Explanation:
4 : 24 and 8 : 48
4 : 24 and 8 ÷ 2 : 48 ÷ 2
4 : 24 and 8 : 48 are equivalent ratios.

Complete.

Question 11.
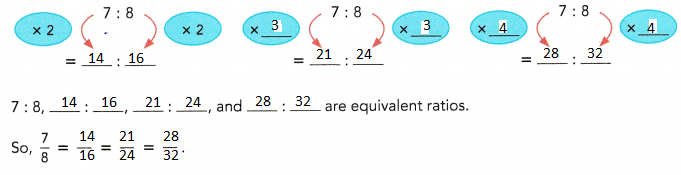
Use multiplication to find three ratios equivalent to 7 : 8.

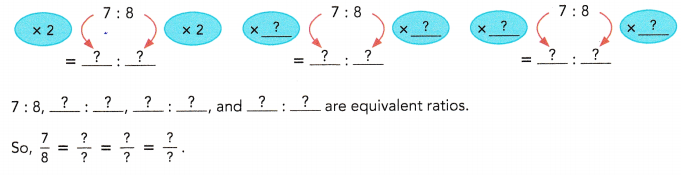
Answer:

Explanation:

Question 12.
Use division to find all the whole number ratios that are equivalent to 24 : 96.

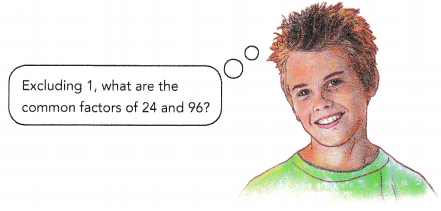
Answer:
24 : 96
Explanation:
24 ÷ 2 : 96 ÷ 2  => 12 : 48
24 ÷ 3 : 96 ÷ 3  => 8  : 32
24 ÷ 4 : 96 ÷ 4  => 6 : 24
24 ÷ 6 : 96 ÷ 6  => 4 : 16
24 ÷ 8 : 96 ÷ 8  => 3 : 12

Find the missing term in each pair of equivalent ratios.

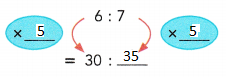
Question 13.

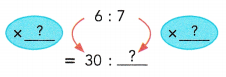
Answer:
30 : 35
Explanation:
6 : 7
multiply both the numbers with 5

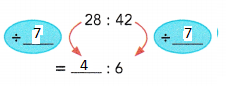
Question 14.

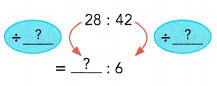
Answer:
4 : 6
Explanation:
4 : 6
multiply both the numbers with 7

Question 15.
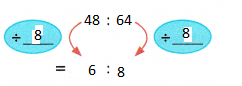
48 : 64 = : 8
Answer: 6
Explanation:
48 : 64
divided both the numbers with 8

Question 16.
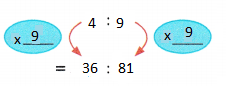
4 : 9 = 36 :
Answer: 81
Explanation:
4 : 9
multiply both the numbers with 9

Solve.

Question 17.
Selena and Drew each has a summer job. The table shows the amount of money they earn, based on the number of hours they work.

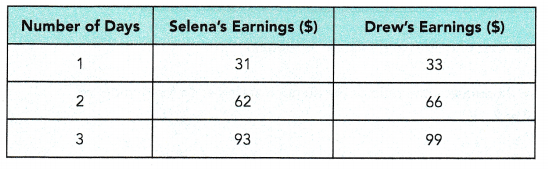
a) Express the ratio of Selena’s earnings to Drew’s earnings in simplest form.
Answer:
31 : 33
Explanation:
Selena and Drew each has a summer job.
for 1 day Selena earns $31
for 1 day Drew earns $33
ratio of Selena’s earnings to Drew’s earnings = 31 : 33

b) If Selena works 4 days, she will earn $.
If Selena works 30 days, she will earn $.
Answer:
$930
Explanation:
If Selena works 4 days, she will earn $124.
for 1 day Selena earns $31
for 4 days = 31 x 4 = 124
If Selena works 30 days, she will earn $930.
31 x 30 = 930

c) If Drew works 4 days, he will earn $.
If Drew works 30 days, he will earn $.
Answer:
If Drew works 4 days, he will earn $132.
If Drew works 30 days, he will earn $990.
Explanation:
for 1 day Drew earns $33
for 4 days = 33 x4 = 132
for 30 days = 30 x 33 = 990

Question 18.
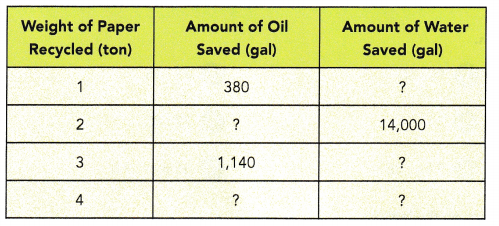
A school organized a paper recycling competition. The table shows the amount of oil and the amount of water saved by recycling paper.

Answer:

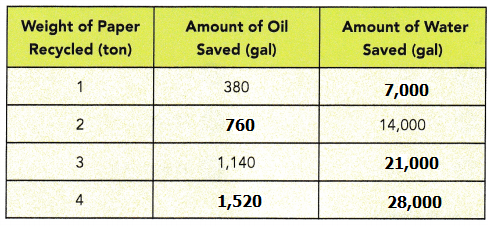
a) How many gallons of water will be saved if 1 ton of paper is recycled?
Answer:
7,000gal
Explanation:
for 2 tons the amount of water saved is 14,000
So, for 1 ton 14000 ÷ 2 = 7000

b) Express the ratio of the amount of oil saved to the amount of water saved in simplest form.
Answer:
19 : 350
Explanation:
Weight of paper recycled for 1 ton =
Amount of oil saved : Amount of water saved
380 : 7000
= 19 : 350

c) How many gallons of oil will be saved if 2 tons of paper are recycled?
Answer:
760gal
Explanation:
for 1 ton of paper recycle need 380gal of oil saved.
for 2 tons oil saved = 380 x 2 = 760

d) How many gallons of water will be saved if 3 tons of paper are recycled?
Answer:
21,000gal
Explanation:
for 1 ton of paper recycle need 7,000gal of water saved.
for 2 tons water saved = 7000 x 3 = 21,000

e) How many gallons of oil and water will be saved if 4 tons of paper are recycled?

Answer:

Explanation:
for 1 ton of paper recycle need 7,000gal of water saved.
for 4 tons water saved = 7000 x 4 = 28,000gal
for 1 ton of paper recycle need 380gal of oil saved.
for 4 tons oil saved = 380 x 4 = 1520gal

Math in Focus Course 1A Practice 4.2 Answer Key

Express each ratio in simplest form.

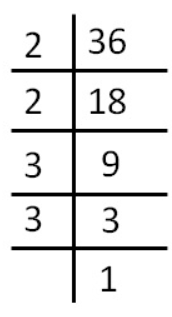
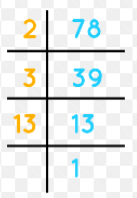
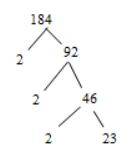
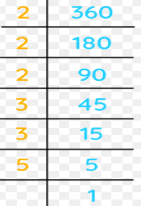
Question 1.
13 : 39
Answer:
1 : 3
Explanation:
13 : 39
common factor for both the numbers is 13
so, 1 : 3

Question 2.
16 : 40
Answer:
2 : 5
Explanation:
16 : 40
common factor for both the numbers is 8
so, 2 : 5

Question 3.
25 : 15
Answer:
5 : 3
Explanation:
25 : 15
common factor for both the numbers is 5
so, 5 : 3

Question 4.
56 : 21
Answer:
8 : 3
Explanation:
56 : 21
common factor for both the numbers is 7
so, 8 : 3

Question 5.
30 : 54
Answer:
5 : 9
Explanation:
30 : 54
common factor for both the numbers is 6
so, 5 : 9

Question 6.
72 : 48
Answer:
8 : 6
Explanation:
72 : 38
common factor for both the numbers is 8
so, 8 : 6

Question 7.
26 cm : 4 m
Answer:
13cm : 200cm
Explanation:
26cm : 4m
convert m in cm
1m = 100 cm
4m = 400cm
26cm : 400cm
common factor for both the numbers is 2
so, 13 : 200

Question 8.
9 kg : 36 g
Answer:
250g : 1g
Explanation:
9kg : 36g
convert kg to g
1kg = 100o g
9kg = 9000g
250g : 1g
common factor for both the numbers is 9
so, 250 : 1

Question 9.
35 min : 2 h
Answer:
7min : 24min
Explanation:
35m : 2h
convert hr in min
1hr = 60min
2hr = 120min
35min : 120min
common factor for both the numbers is 5
so, 7 : 24

State whether each pair of ratios are equivalent.

Question 10.
11 : 17 and 17 : 11
Answer:
No, pair of ratios are not equal
Explanation:
11 : 17 and 17 : 11
the given numbers are not equivalent to their ratios.

Question 11.
7 : 11 and 21 : 33
Answer:
YES, pair of ratios are equal.
Explanation:
7 : 11 and 21 : 33
The common factor for both the numbers is 3
So, both are equivalent.

Question 12.
15 : 35 and 25 : 45
Answer:
NO, pair of ratios are not equal.
Explanation:
15 : 35 and 25 : 45
3 : 7  and 5 : 9
The common factor for both the numbers is 5
So, both are not equivalent.

Question 13.
15 : 20 and 20 : 25
Answer:
NO, pair of ratios are not equal.
Explanation:
15 : 20 and 20 : 25
3 : 4 and 4 : 5
So, both are not equivalent.

Question 14.
38 : 19 and 2 : 1
Answer:
NO, pair of ratios are not equal.
Explanation:
38 : 19 and 2 : 1
2:1 and 1:2 [19 x 2 =38 and 19 x 1 = 19]
So, both are not equivalent.

Question 15.
12 : 8 and 18 : 12
Answer:
YES, pair of ratios are equal.
Explanation:
12 : 8 and 18 : 12
3 : 2 and 3 : 2
So, both are equivalent.

Find the missing term in each pair of equivalent ratio.

Question 16.
7 : 9 = 49 :
Answer: 63
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 7, b = 9, c = 49, d = x
7 x x = 9 x 49
7x = 441
x = \(\frac{441}{7}\)
x = 63

Question 17.
12 : 5 = 144 :
Answer: 60
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a =12, b = 5, c = 144, d = x
12 x x = 5 x 144
12x = 720
x = \(\frac{720}{12}\)
x = 60

Question 18.
4 : 15 = 48 :
Answer: 180
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 4, b = 15, c = 48, d = x
4 x x = 15 x 48
4x = 720
x = \(\frac{720}{4}\)
x = 180

Question 19.
7 : 13 = 77 :
Answer: 143
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 7, b = 13, c = 77, d = x
7 x x = 13 x 77
7x = 1,001
x = \(\frac{1001}{7}\)
x = 143

Question 20.
45 : 36 = : 12
Answer: 15
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 45, b = 36, c = x, d = 12
45 x 12 = 36 x x
36x = 540
x = \(\frac{540}{36}\)
x = 15

Question 21.
30 : 48 = : 8
Answer: 5
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 30, b = 48, c = x, d = 8
30 x 8 = 48 x x
48x = 240
x = \(\frac{240}{48}\)
x = 5

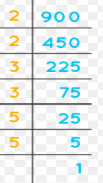
Question 22.
72 : 84 = : 7
Answer: 6
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 72, b = 84, c = x, d = 7
72 x 7 = 84 x x
504 = 84x
x = \(\frac{504}{84}\)
x = 6

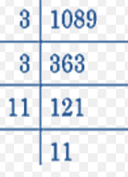
Question 23.
121 : 88 = : 8
Answer: 11
Explanation
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 121, b = 88, c = x, d = 8
121 x 8 = 88 x x
88x = 968
x = \(\frac{968}{88}\)
x = 11

Find the equivalent ratios.

Question 24.
Use multiplication to find three ratios equivalent to 8 : 12.
Answer:
The three equivalent ratios of 8 : 12 are 16 : 24; 24: 36 and 32 : 48.
Explanation:
first we need to write the given ratio as fraction = 8/12
= (8 × 2)/(12 × 2)
= 16/24
= 16 : 24 (one equivalent ratio),
So, 16 : 24 is an equivalent ratio of 8 : 12.
Similarly again, we need to write the given ratio 8 : 12 as fraction to get another equivalent ratio = 8/12
= (8 × 3)/(12 × 3)
= 24/36 is another equivalent ratio.
Similarly again, we need to write the given ratio 8 : 12 as fraction to get another equivalent ratio = 8/12
= (8 × 4)/(12 × 4)
= 32/48 is another equivalent ratio.
Therefore, the three equivalent ratios of 8 : 12 are 16 : 24; 24: 36 and 32 : 48.

Question 25.
Use division to find all the whole number ratios equivalent to 168 : 56.
Answer:
84 : 28; 56: 18 and 42 : 14.
Explanation:
first we need to write the given ratio as fraction = 168/56
= (168 ÷ 2)/(56 ÷ 2)
= 84/28
So, 168 : 56 is an equivalent ratio of 84 : 28.
Similarly again, we need to write the given ratio 168 : 56 as fraction to get another equivalent ratio = 168/56
= (168 ÷ 3)/(56 ÷ 3)
= 56/18
So, 168 : 56 is an equivalent ratio of 56 : 18.
Similarly again, we need to write the given ratio 168 : 56 as fraction to get another equivalent ratio = 168/56
= (168 ÷ 4)/(56 ÷ 4)
= 42/14
So, 168 : 56 is an equivalent ratio of 42 : 14.
Therefore, the two equivalent ratios of 168 : 56 are 84 : 28; 56: 18 and 42 : 14.

Copy and complete.

Question 26.
A manufacturer’s instruction states that 3 cups of cleaning agent should be diluted with 5 cups of water before use. Copy and complete the table.

Answer:

Explanation:
A manufacturer’s instruction states that 3 cups of cleaning agent should be diluted with 5 cups of water before use.
ratio of cleaning agent and water = 3 : 5

Find the missing term of each pair of equivalent ratio.

Question 27.
63 : 27 = 49 :
Answer: 21
Explanation:
the product of extremes = the product of means
a:b :: c:d  = > a x d = b x c
(27 x 49) /63 = 21
63 : 27 = 49 : 21

Question 28.
81 : 18 = 36 :
Answer: 8
Explanation:
the product of extremes = the product of means
a:b :: c:d  = > a x d = b x c
(18 x 36) /81 = 648/81 = 8
81 : 18 = 36 : 8

Question 29.
24 : 96 = 5 :
Answer: 20
Explanation:
the product of extremes = the product of means
a:b :: c:d  = > a x d = b x c
(96 x 5) /24 = 480/24 = 20
24 : 96 = 5 : 20

Question 30.
72 : 24 = 15 :
Answer: 5
Explanation:
the product of means = the product of extremes
a:b :: c:d  = > a x d = b x c
(24 x 15) /72 = 360/72 = 5
72 : 24 = 15 : 5

Question 31.
60 : 144 = : 60
Answer: 25
Explanation:
the product of means = the product of extremes
a:b :: c:d  = > a x d = b x c
(60 x 60) /144= 3600/144 = 25
60 : 144 = 25 : 60

Question 32.
125 : 80 = : 48
Answer: 75
Explanation:
the product of extremes = the product of means
a:b :: c:d  = > a x d = b x c
(125 x 48) /80 = 6000/80 = 75
125 : 80 = 75 : 48

Question 33.
90 : 15 = : 7
Answer: 42
Explanation:
the product of extremes = the product of means
a:b :: c:d  = > a x d = b x c
(90 x 7) /15 = 630/15 = 42
90 : 15 = 42 : 7

Question 34.
98 : 112 = 63 :
Answer: 72
Explanation:
the product of extrems = the product of means
a:b :: c:d  = > a x d = b x c
(112 x 63) /98 = 7056/98 = 72
98 : 112 = 63 : 72

Solve.

Question 35.
Judy uses 5 ounces of lemonade concentrate for every 9 ounces of orange juice concentrate to make a fruit punch.

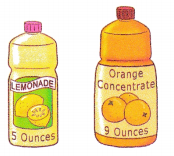
a) Find the ratio of the number of ounces of orange juice concentrate to the number of ounces of lemonade concentrate she uses.
Answer:
9 : 5
Explanation:
Judy uses 5 ounces of lemonade concentrate for every 9 ounces of orange juice concentrate to make a fruit punch.
The ratio of the orange juice and lemonade = 9 : 5

b) If Judy uses 36 ounces of orange juice concentrate to make the fruit punch, how many ounces of lemonade concentrate does she use?
Answer:
20 oz
Explanation:
If Judy uses 36 ounces of orange juice concentrate to make the fruit punch,
how many ounces of lemonade concentrate does she use
9 : 5 = 36 : ?
the product of means = the product of extremes
a:b :: c:d  = > a x d = b x c
(36 x 5) /9 = 180/9 = 20
9 : 5 = 36 : 20

c) If Judy uses 45 ounces of lemonade concentrate to make the fruit punch, how many ounces of orange juice concentrate does she use?
Answer:
81 oz
Explanation:
If Judy uses 45 ounces of lemonade concentrate to make the fruit punch,
how many ounces of orange juice concentrate does she use
9 : 5 = ? : 45
the product of means = the product of extremes
a:b :: c:d  = > a x d = b x c
(9 x 45) /5 = 405/5 = 81
9 : 5 = 81 : 45

Question 36.
In a science experiment, Farah mixed a salt solution and vinegar in the ratio 3 : 7.
a) If she used 262.8 milliliters of salt solution1 how much vinegar did she use?
Answer:
183.9ml
Explanation:
The ratio of vinegar to total mixture is 7 : 10
The 10 is 3 + 7.  Out of 10 ml, 3 will be Salt and 7 will be Vinegar.
7/10 = V/262.8
1839.6 = 10V
V = 183.9 ml

b) If 0.56 liter of vinegar was used, how much salt solution did she use?
Answer:
78.84 ml
Explanation:
The ratio of salt to total mixture is 3 : 10
The 10 is 3 + 7.  Out of 10 ml, 3 will be Salt and 7 will be Vinegar.
3/10 = Salt/262.8
262.8 x 3 = 10S
788.4 = 10S
S = 788.4/10
S = 78.84 ml

Question 37.
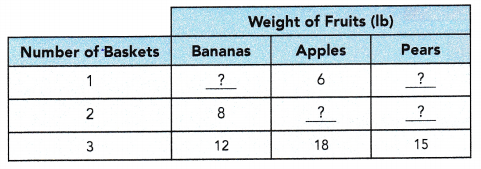
A fruit seller packs different fruits into baskets of the same size. The ratio of the weight of bananas to the weight of apples to the weight of pears s the same for all the baskets. The table shows the different weights of fruits in the baskets. Copy and complete the table.

Answer:

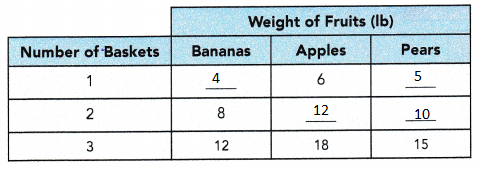
Explanation:
A fruit seller packs different fruits into baskets of the same size.
The ratio of the weight of bananas to the weight of apples to the weight of pears are the same for all the baskets.
The table shows the different weights of fruits in the baskets.
Find the largest common factor, of all the fruits.
46 apples = 8 x 6
30 pears = 5 x 6
24 bananas = 4 x 6
6 baskets each with 8 apples, 5 pears and 4 bananas.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Review Test to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Review Test Answer Key

Concepts and Skills

Divide.

Question 1.
15 ÷ \(\frac{1}{3}\)

Answer: 45
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

\(\frac{15}{1}\) ÷ \(\frac{1}{3}\)

\(\frac{15}{1}\) x \(\frac{3}{1}\)

15 x 3 = 45

Question 2.
24 ÷ \(\frac{1}{6}\)

Answer: 144
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

24 ÷ \(\frac{1}{6}\)

24 x 6 = 144

Question 3.
\(\frac{3}{8}\) ÷ \(\frac{3}{4}\)

Answer:
\(\frac{1}{2}\)

Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

\(\frac{3}{8}\) ÷ \(\frac{3}{4}\)

\(\frac{3}{8}\) x \(\frac{4}{3}\)

\(\frac{12}{24}\) = \(\frac{1}{2}\)

Question 4.
\(\frac{7}{12}\) ÷ \(\frac{1}{3}\)

Answer:

Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

\(\frac{7}{12}\) ÷ \(\frac{1}{3}\)

\(\frac{7}{12}\) x \(\frac{3}{1}\)

\(\frac{21}{12}\) = \(\frac{7}{3}\)

Multiply.

Question 5.
0.3 × 8
Answer: 2.4
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.3 x 8 = 2.4

Question 6.
6 × 0.7
Answer: 4.2
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
6 x 0.7 = 4.2

Question 7.
0.28 × 6
Answer: 1.68
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.28 x 6 = 1.68

Question 8.
7 × 0.068
Answer: 0.476
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
7 x 0.068 = 0.476

Question 9.
0.3 × 0.6
Answer: 0.18
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.3 x 0.6 = 0.18

Question 10.
0.5 × 0.8
Answer: 0.4
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
0.5 x 0.8 = 0.4

Question 11.
5.7 × 0.4
Answer: 2.28
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
5.7 x 0.4 = 2.28

Question 12.
9.3 × 0.89
Answer: 8.277
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
then the number of decimal places in the product is equal to the total number of decimal places in both the given numbers.
9.3 x 0.89 = 8.277

Divide.

Question 13.
6 ÷ 0.6
Answer: 10
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.
6 ÷ 0.6 = 10

Question 14.
8 ÷ 0.4
Answer: 20
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 15.
35 ÷ 0.7
Answer: 50
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 16.
88 ÷ 0.2
Answer: 440
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 17.
5 ÷ 0.25
Answer: 20
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 18.
8 ÷ 0.16
Answer: 50
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 19.
96 ÷ 0.16
Answer: 600
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 20.
396 ÷ 0.36
Answer: 1,100
Explanation:
To divide a number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 21.
0.87 ÷ 0.03
Answer: 29
Explanation:
To divide a decimal number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Question 22.
0.98 ÷ 0.7
Answer: 1.4
Explanation:
To divide a decimal number by a decimal number,
multiply the divisor by as many tens as necessary until we get a whole number,
then remember to multiply the dividend by the same number of tens.

Problem Solving

Solve. Show your work.

Question 23.
In January, Jane volunteered at a hospital for a total of 12 hours. She spent \(\frac{4}{5}\) hour at the hospital every time she volunteered. How many times did Jane volunteer in January?
Answer:
15 times
Explanation:
In January, Jane volunteered at a hospital for a total of 12 hours.
She spent \(\frac{4}{5}\) hour at the hospital every time she volunteered.
Number times Jane volunteer in January
\(\frac{12}{1}\) ÷ \(\frac{4}{5}\)

\(\frac{12}{1}\) x \(\frac{5}{4}\)
3 x 5 = 15

Question 24.
Paul is making loaves of raisin bread to sell at a fundraising event. The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf, and Paul has 3\(\frac{1}{4}\) cups of raisins.
a) How many loaves can Paul make?
Answer:
Paul can make 9 loaves.
Explanation:
Paul has 3\(\frac{1}{4}\) cups of raisins.

The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf,

Number of loaves can Paul make are

\(\frac{13}{4}\) ÷ \(\frac{1}{3}\)

\(\frac{13}{4}\) x \(\frac{3}{1}\)

39 ÷ 4 = 9\(\frac{3}{4}\)

b) How many cups of raisins will he have left over?
Answer:
\(\frac{3}{4}\)

Explanation:
Paul has 3\(\frac{1}{4}\) cups of raisins.

The recipe calls for \(\frac{1}{3}\) cup of raisins for each loaf,
Number of loaves can Paul make are

\(\frac{13}{4}\) ÷ \(\frac{1}{3}\)

\(\frac{13}{4}\) x \(\frac{3}{1}\)

39 ÷ 4 = 9\(\frac{3}{4}\)

Number of loaves left over are \(\frac{3}{4}\)

Question 25.
Jane has a dog that eats 0.8 pound of dog food each day. She buys a 40-pound bag of dog food. How many days will this bag of dog food last?
Answer:
50 days
Explanation:
Jane has a dog that eats 0.8 pound of dog food each day.
She buys a 40-pound bag of dog food.
Number of days will this bag of dog food last

Question 26.
Mervin had some cartons of milk. He sold \(\frac{2}{5}\) of the cartons of milk in the morning. He then sold \(\frac{3}{4}\) of the remainder in the afternoon. 24 more cartons of milk were sold in the afternoon than in the morning. How many cartons of milk did Mervin have at first?
Answer:
480 cartons of milk.
Explanation:
total 5 parts
each part can be sub divided in to 4 parts each
in each  box 24 cartons of milk
if total boxes are 20 and each box contains 24 cartons of milk
then the total number of milk is 24 x 20 = 480

Question 27.
Alice baked a certain number of pies. She gave \(\frac{1}{8}\) of the pies to her friends and \(\frac{1}{4}\) of the remainder to her neighbor. She was left with 63 pies. How many pies did Alice bake at first?
Answer:
96 pies
Explanation:
Let the original count of pies be represented by $x$She gave \(\frac{1}{8}\) of the pies to her friend

Question 28.
At a concert, \(\frac{2}{5}\) of the people were men. There were 3 times as many women as children. If there were 45 more men than children, how many people were there at the concert?
Answer:
180 people
Explanation:
Let people= p
men = \(\frac{2}{5}\)p
Let children = c
women = 3c
men = \(\frac{2}{5}\)p = c+45
people = men + women + children
= \(\frac{2}{5}\)p + 3c + c

= \(\frac{2}{5}\)p + 4c

= \(\frac{3}{5}\)p = 4c
\(\frac{2}{5}\)p = c + 45
Children = 27
people = 180
So, 180 people at the show.
women = 3c = 3 x 27 = 81
men = \(\frac{2}{5}\)p = c+45
= 72

Question 29.
\(\frac{3}{4}\) of the students in a school were girls and the rest were boys. \(\frac{2}{3}\) of the girls and \(\frac{1}{2}\) of the boys attended the school carnival. Find the total number of students in the school if 330 students did not attend the carnival.
Answer:
Total number of students 880
Explanation:
girls = 3boys,
since \(\frac{3}{4}\) = 3 x \(\frac{1}{4}\)

\(\frac{2}{3}\) girls + \(\frac{1}{2}\) boys attended

\(\frac{2}{3}\) x 3boys + \(\frac{1}{2}\) boys

= \(\frac{5}{2}\) boys attended

subtract that from the total (boys + girls) students:
boys + girls – \(\frac{5}{2}\) boys = 330

4b – \(\frac{5}{2}\) boys = 330

\(\frac{3}{2}\) boys = 330
boys = 220
so, girls = 3b
= 220 x 3 = 660
Boys + Girls = (220 + 660) = 880
There are 880 students
660 girls and 220 boys
440 girls and 110 boys attended = 550
the remaining 330 did not attend.

Question 30.
At a baseball game, there were three times as many males as females. \(\frac{5}{6}\) of the males were boys and the rest were men. \(\frac{2}{3}\) of the females were girls and the rest were women. Given that there were 121 more boys than girls, how many adults were there at the baseball game?
Answer:
55 adults
Explanation:
Number of females x
Number of girls = \(\frac{2}{3}\) x – girls

Number of women = \(\frac{1}{3}\) x

Number of males = 3x

Number of boys = \(\frac{5}{6}\) x 3x

= \(\frac{5}{2}\) x – boys

Number of men = \(\frac{1}{6}\) x 3x

= \(\frac{1}{2}\) x – men
So, \(\frac{5}{2}\) – 121 = \(\frac{2}{3}\) x

\(\frac{15}{6}\)x – \(\frac{4}{6}\)x = 121

\(\frac{11}{6}\)x = 121
x = 66
Men = \(\frac{1}{2}\) x 66 = 33

Women = \(\frac{1}{3}\) x 66 = 22
Adults = Men + Women
Adults = 33 + 22 = 55
Question 31.
Mr. Thomas spent $1,600 of his savings on a television set and \(\frac{2}{5}\) of the remainder on a refrigerator. He had \(\frac{1}{3}\) of his original amount of savings left.
a) What was Mr. Thomas’s original savings?
Answer:
$3600
b) What was the cost of the refrigerator?
Answer:
$2400
Explanation:
Let $\mathrm{x\; is\; the\; savings,}$x−(1600+(2x− \(\frac{1600}{5}\)) = x3
Because x is total amount of savings and he spent $1600
So, now he has $2÷5$ of the total amount – $1600
($x÷3$ Because he has $1÷3$ of his original amount of savings)
$x+(-1600-\frac{2x-\; \backslash (\backslash frac\{3200\}\{5\}\backslash )}{})$ = $\frac{x}{3}$3x+3(−1600+−2x+ \(\frac{3200}{5}\))=x
3x+(−4800+−6x+ \(\frac{9600}{5}\))=x
3x+(−4800−1.2x+1920)=x
2x=4800+1.2x−1920.
8x=2880
x=3600

Question 32.
Sue buys 8.5 pounds of chicken to make tacos. She uses 0.3 pound of chicken for each taco.
a) How many tacos can Sue make?
Answer:
Sue can make 28 tacos
b) How many pounds of chicken are left over?
Answer:
\(\frac{1}{3}\) left over
Explanation:
Sue buys 8.5 pounds of chicken to make tacos.
She uses 0.3 pound of chicken for each taco.
\(\frac{8.5}{0.3}\)
= 28 \(\frac{1}{3}\)

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Lesson 3.2 Multiplying Decimals to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Lesson 3.2 Answer Key Multiplying Decimals

Math in Focus Grade 6 Chapter 3 Lesson 3.2 Guided Practice Answer Key

Complete.

Question 1.
Multiply 0.9 by 4.

Answer:
The multiplication of  0.9 by 4 is 3.6.

Explanation:
The multiplication of  0.9 by 4 is 3.6.

Question 2.
Multiply 0.025 by 3.

Answer:

Explanation:
The multiplication of 0.025 by 3 is 0.075.

Multiply.

Question 3.

Answer:
The multiplication of 0.07 × 9 is 0.63.

Explanation:
The multiplication of 0.07 × 9 is 0.63.

Question 4.

Answer:
The multiplication of 0.14 × 3 is 0.42.

Explanation:
The multiplication of 0.14 × 3 is 0.42.

Question 5.

Answer:
The multiplication of 0.045 × 7 is 0.315.

Explanation:
The multiplication of 0.045 × 7 is 0.315.

Write in vertical form. Then multiply and decide where to place the decimal point.

Question 6.
0.32 × 8
Answer:
0.32 × 8 = 2.56.

Explanation:
The multiplication of 0.32 × 8 is 2.56.

Question 7.
9 × 0.24
Answer:
9 × 0.24 = 2.16.

Explanation:
The multiplication of 9 × 0.24 is 2.16.

Question 8.
0.057 × 6
Answer:
0.057 × 6 = 0.342.

Explanation:
The multiplication of 0.057 × 6 is 0.342.

Complete.

Question 9.
Find 0.3 × 0.6.

Answer:
The multiplication of 0.3 × 0.6 is 0.18.

Explanation:
The multiplication of 0.3 × 0.6 is
0.3 × 0.6 = \(\frac{3}{10}\) × \(\frac{6}{10}\)
= \(\frac{18}{100}\)
= 0.18.

Question 10.
Find 0.9 × 0.8.

Answer:
The multiplication of 0.9 × 0.8 is 0.72.

Explanation:
The multiplication of 0.9 × 0.8 is

Complete.

Question 11.
Find 3.2 × 0.6

Answer:
The multiplication of 3.2 × 0.6 is 1.92.

Explanation:
The multiplication of 3.2 × 0.6 is

Write in vertical form. Then multiply and decide where to place the decimal point.

Question 12.
4.3 × 5.7
Answer:
The multiplication of 4.3 × 5.7 is 24.51.

Explanation:
The multiplication of 4.3 × 5.7 is

Complete.

Question 13.
Find 0.89 × 0.4

Answer:
The multiplication of 0.89 × 0.4 is 0.356.

Explanation:
The multiplication of 0.89 × 0.4 is

Write in vertical form. Then multiply and decide where to place the decimal point.

Question 14.
4.3 × 5.7
Answer:
The multiplication of 4.3 × 5.7 is 24.51.

Explanation:
The multiplication of 4.3 × 5.7 is

Hands-On Activity

Materials

• graph paper
• ruler

Finding the factors of a decimal.

Step 1.
Draw four 10 × 10 squares on graph paper.

Step 2.
Mark each side from 0 to 1 as shown.

Step 3.
a) Find two decimals that give a product of 0.12.
× = 0.12
Show and shade 0.12 on the grids in two different ways.
Example
0.2 × 0.6 = 0.12

Answer:

b) Find two decimals that give a product of 0.36. Show and shade 0.36 on the grids in two different ways.
Answer:
0.6 × 0.6 = 0.36.

Explanation:
The two decimals that give a product of 0.36 is 0.6 × 0.6.

Math in Focus Course 1A Practice 3.2 Answer Key

Complete.

Question 1.
0.3 × 4 is the same as groups of .
Answer:
0.3 groups of 4.

Explanation:
Here 0.3 × 4 is the same as 0.3 groups of 4.

Question 2.
7 × 0.8 is the same as groups of .
Answer:
7 groups of 0.8.

Explanation:
Here 7 × 0.8 is the same as 7 groups of 0.8.

Write a multiplication statement that represents each number line.

Question 3.

Answer:
3×0.5 = 1.5.

Explanation:
The multiplication statement that represents the number line is 3×0.5 = 1.5.

Question 4.

Answer:
6×0.9 = 5.4.

Explanation:
The multiplication statement that represents the number line is 6×0.9 = 5.4.

Write in vertical form. Then multiply.

Question 5.
0.9 × 12
Answer:
The multiplication of 0.9 × 12 is 10.8.

Explanation:
The multiplication of 0.9 × 12 is
9                          0.9
×  12                       × 12
_____               ———
108                     10.8

Question 6.
0.47 × 5
Answer:
The multiplication of 0.47 × 5 is 2.35.

Explanation:
The multiplication of 0.47 × 5 is
47 × 5 = 235
0.47 × 5 = 2.35

Question 7.
0.063 × 9
Answer:
0.063 × 9 = 0.67.

Explanation:
The multiplication of 0.063 × 9 is
63 × 9 = 567
0.063 × 9 = 0.567.

Question 8.
00.85 × 11
Answer:
The multiplication of 00.85 × 11 is  9.35.

Explanation:
The multiplication of 00.85 × 11 is
85 × 11 = 935,
00.85 × 11 = 9.35.

Question 9.
00.1 × 0.2
Answer:
The multiplication of 00.1 × 0.2 is 0.02.

Explanation:
The multiplication of 00.1 × 0.2 is
1 × 2 = 2,
00.1 × 0.2 = 0.02.

Question 10.
0.2 × 0.3
Answer:
The multiplication of 0.2 × 0.3 is

Explanation:
The multiplication of 0.2 × 0.3 is
2 × 3 = 6
0.2 × 0.3 = 0.06.

Question 11.
0.4 × 0.4
Answer:
The multiplication of 0.4 × 0.4 is 0.16.

Explanation:
The multiplication of 0.4 × 0.4 is
4 × 4 = 16,
0.4 × 0.4 = 0.16.

Question 12.
0.6 × 0.7
Answer:
The multiplication of 0.6 × 0.7 is 0.42.

Explanation:
The multiplication of 0.6 × 0.7 is
6 × 7 = 42,
0.6 × 0.7 = 0.42.

Question 13.
0.7 × 0.9
Answer:
The multiplication of 0.7 × 0.9 is 0.63.

Explanation:
The multiplication of 0.7 × 0.9 is
7 × 9 = 63,
0.7 × 0.9 = 0.63.

Multiply mentally.

Question 14.
0.7 × 8
Answer:
The mental multiplication of 0.7 × 8 is 5.6.

Explanation:
The mental multiplication of 0.7 × 8 is
0.7 × 8 = \(\frac{7}{10}\) × 8
= \(\frac{7}{5}\) × 4
= \(\frac{28}{5}\)
= 5.6.

Question 15.
0.9 × 9
Answer:
The mental multiplication of 0.9 × 9 is 8.1.

Explanation:
The mental multiplication of 0.9 × 9 is
0.9 × 9 = \(\frac{9}{10}\) × 9
= \(\frac{81}{10}\)
= 8.1.

Question 16.
0.9 × 11
Answer:
The mental multiplication of 0.9 × 11 is 9.9.

Explanation:
The mental multiplication of 0.9 × 11 is
0.9 × 11 = \(\frac{9}{10}\) × 11
= \(\frac{99}{10}\)
= 9.9.

Question 17.
0.7 × 0.4
Answer:
The mental multiplication of 0.7 × 0.4 is \(\frac{14}{50}\).

Explanation:
The mental multiplication of 0.7 × 0.4 is
0.7 × 0.4 = \(\frac{7}{10}\) × \(\frac{4}{10}\)
= \(\frac{7}{10}\) × \(\frac{2}{5}\)
= \(\frac{14}{50}\).

Question 18.
0.8 × 0.6
Answer:
The mental multiplication of 0.8 × 0.6 is 0.48.

Explanation:
The mental multiplication of 0.8 × 0.6 is
0.8 × 0.6 = \(\frac{8}{100}\) × \(\frac{6}{100}\)
= \(\frac{48}{100}\)
= 0.48.

Question 19.
0.3 × 0.9
Answer:
The mental multiplication of 0.3 × 0.9 is 0.27.

Explanation:
The mental multiplication of 0.3 × 0.9 is
0.3 × 0.9 = \(\frac{3}{100}\) × \(\frac{9}{100}\)
= \(\frac{27}{100}\)
= 0.27.

Question 20.
0.7 × 0.7
Answer:
The mental multiplication of 0.7 × 0.7 is 0.49.

Explanation:
The mental multiplication of 0.7 × 0.7 is
0.7 × 0.7 = \(\frac{7}{100}\) × \(\frac{7}{100}\)
= \(\frac{49}{100}\)
= 0.49.

Question 21.
0.5 × 0.9
Answer:
The mental multiplication of 0.5 × 0.9 is 0.45.

Explanation:
The mental multiplication of 0.5 × 0.9 is
0.5 × 0.9 = \(\frac{5}{10}\) × \(\frac{9}{10}\)
= \(\frac{45}{100}\)
= 0.45.

Question 22.
0.8 × 0.9
Answer:
The mental multiplication of 0.8 × 0.9 is 0.72.

Explanation:
The mental multiplication of 0.5 × 0.9 is
0.8 × 0.9 = \(\frac{8}{10}\) × \(\frac{9}{10}\)
= \(\frac{72}{100}\)
= 0.72.

Question 23.
0.15 × 6
Answer:
The mental multiplication of 0.15 × 6 is 0.9.

Explanation:
The mental multiplication of 0.15 × 6 is
0.15 × 6 = \(\frac{15}{100}\) × \(\frac{6}{10}\)
= \(\frac{90}{100}\)
= 0.9

Question 24.
0.22 × 4
Answer:
The mental multiplication of 0.22 × 4 is 0.88.

Explanation:
The mental multiplication of 0.22 × 4 is
0.22 × 4 = \(\frac{22}{100}\) ×4
= \(\frac{88}{100}\)
= 0.88.

Question 25.
0.25 × 3
Answer:
The mental multiplication of 0.25 × 3 is 0.75.

Explanation:
The mental multiplication of 0.25 × 3 is
0.25 × 3 = \(\frac{25}{100}\) × 3
= \(\frac{75}{100}\)
= 0.75.

Question 26.
0.032 × 5
Answer:
The mental multiplication of 0.032 × 5 is 0.16.

Explanation:
The mental multiplication of 0.032 × 5 is
0.032 × 5 = \(\frac{32}{1000}\) × 5
= \(\frac{160}{1000}\)
= 0.16.

Question 27.
0.04 1 × 8
Answer:
The mental multiplication of 0.04 1 × 8 is 0.328.

Explanation:
The mental multiplication of 0.04 1 × 8 is
0.04 1 × 8 = \(\frac{41}{1000}\) × 8
= \(\frac{41}{1000}\) × 8
= \(\frac{328}{1000}\)
= 0.328.

Question 28.
0.055 × 9
Answer:
The mental multiplication of 0.055 × 9 is 0.495.

Explanation:
The mental multiplication of 0.055 × 9 is
0.055 × 9 = \(\frac{55}{1000}\) × 9
= \(\frac{495}{1000}\)
= 0.495.

Write in vertical form. Then multiply.

Question 29.
1.2 × 0.6
Answer:
The multiplication of 1.2 × 0.6 is 0.72.

Explanation:
The multiplication of 1.2 × 0.6 is
12 × 06 = 72,
1.2 × 0.6 = 0.72.

Question 30.
0.89 × 1.2
Answer:
The multiplication of 0.89 × 1.2 is 1.068.

Explanation:
The multiplication of 0.89 × 1.2 is
89 × 12 = 1,068,
0.89 × 1.2 = 1.068.

Question 31.
2.3 × 1.5
Answer:
The multiplication of 2.3 × 1.5 is 3.45.

Explanation:
The multiplication of 2.3 × 1.5 is
23 × 15 = 345,
2.3 × 1.5 = 3.45.

Question 32.
3.4 × 6.7
Answer:
The multiplication of 3.4 × 6.7 is 22.78.

Explanation:
The multiplication of 3.4 × 6.7 is
34 × 67 = 2,278.
3.4 × 6.7 = 22.78.

Question 33.
4.9 × 6.3
Answer:
The multiplication of 4.9 × 6.3 is 30.87.

Explanation:
The multiplication of 4.9 × 6.3 is
49 × 63 = 3,087,
4.9 × 6.3 = 30.87.

Question 34.
5.8 × 7.8
Answer:
The multiplication of 5.8 × 7.8 is 45.24.

Explanation:
The multiplication of 5.8 × 7.8 is
58 × 78 = 4,524,
5.8 × 7.8 = 45.24.

Question 35.
0.46 × 1.3
Answer:
The multiplication of 0.46 × 1.3 is 0.598.

Explanation:
The multiplication of 0.46 × 1.3 is
46 × 13 = 598.
0.46 × 1.3 = 0.598.

Question 36.
0.705 × 0.5
Answer:
The multiplication of 0.705 × 0.5 is 0.3525.

Explanation:
The multiplication of 0.705 × 0.5 is
705 × 5 = 3,525,
0.705 × 0.5 = 0.3525.

Question 37.
0.597 × 0.21
Answer:
The multiplication of 0.597 × 0.21 is 0.12537.

Explanation:
The multiplication of 0.597 × 0.21 is
597 × 21 = 12,537,
0.597 × 0.21 = 0.12537.

Question 38.
Math Journal Your friend knows how to find the product \(\frac{57}{100}\) × \(\frac{3}{10}\). However, your friend does not know how to find the product 0.57 × 0.3. Write an explanation that will help your friend understand how to multiply the two decimals.
Answer:
Here the product of \(\frac{57}{100}\) × \(\frac{3}{10}\) is \(\frac{171}{100}\) which is 1.71 and to find the product of 0.57 × 0.3 first we will multiply 57 × 3 which is 171 and then we will place decimal, so the product will be 1.71.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Lesson 3.1 Dividing Fractions to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Lesson 3.1 Answer Key Dividing Fractions

Math in Focus Grade 6 Chapter 3 Lesson 3.1 Guided Practice Answer Key

Solve.

Question 1.
Rina cut 3 paper squares into a number of equal pieces. Each piece was \(\frac{1}{6}\) of a square. Into how many pieces did Rina cut the 3 paper squares?


The model shows that:
Number of one-sixths in 1 paper square =
Number of one-sixths in 3 paper squares = ×

Answer:
Rina cut the 3 paper squares into 18 pieces.

Explanation:
Given that Rina cut 3 paper squares into a number of equal pieces and each piece was \(\frac{1}{6}\) of a square. So the number of many pieces did Rina cut the 3 paper squares is 3 ÷ \(\frac{1}{6}\)
= 3 × 6
= 18 pieces.

Divide.

Question 2.
3 ÷ \(\frac{1}{5}\) =
Answer:
3 ÷ \(\frac{1}{5}\) = 15.

Explanation:
The division of 3 ÷ \(\frac{1}{5}\)  is 3 × 5 = 15.

Question 3.
7 ÷ \(\frac{1}{4}\) =
Answer:
7 ÷ \(\frac{1}{4}\) = 28.

Explanation:
The division of 7 ÷ \(\frac{1}{4}\) is 7 × 4 = 28.

Question 4.
4 ÷ \(\frac{1}{2}\) =
Answer:
4 ÷ \(\frac{1}{2}\) = 8.

Explanation:
The division of 4 ÷ \(\frac{1}{2}\) is 4 × 2 = 8.

Question 5.
5 ÷ \(\frac{1}{3}\) =
Answer:
5 ÷ \(\frac{1}{3}\) = 15.

Explanation:
The division of 5 ÷ \(\frac{1}{3}\) is 5 × 3 = 15.

Question 6.
6 ÷ \(\frac{1}{5}\) =
Answer:
6 ÷ \(\frac{1}{5}\) = 15.

Explanation:
The division of 6 ÷ \(\frac{1}{5}\) is 6 × 5 = 15.

Question 7.
8 ÷ \(\frac{1}{8}\) =
Answer:
8 ÷ \(\frac{1}{8}\) = 64.

Explanation:
The division of 8 ÷ \(\frac{1}{8}\) is 8 × 8 = 64.

Hands-On

Activity Materials:

• 5 paper strips

Dividing Whole Numbers By A Fraction

Use 5 paper strips of the same size and length. Each strip represents 1 whole.

Step 1.
Take 2 paper strips. Divide each of them into thirds using vertical lines and place them as shown. Then find 2 ÷ \(\frac{2}{3}\)

Refer to your model.
Complete:
There are two-thirds in the 2 paper strips.
So, 2 ÷ \(\frac{2}{3}\) = .

Step 2.
Divide each of the other 3 paper strips into fourths using vertical lines and place them as shown. Then find 3 ÷ \(\frac{3}{4}\).

Refer to your model.
Complete:
There are three-fourths in the 3 paper strips.
So, 3 ÷ \(\frac{3}{4}\) = .

Complete:

Question 8.
Find 7 ÷ \(\frac{3}{4}\)

Question 9.
Mrs. Johnson bought 6 pizzas. She cut them into many equal pieces for the students in her class. Each piece was \(\frac{3}{10}\) of a whole pizza. How many students were there in the class if each child received only one piece of pizza?

Answer:
There were 20 students in the class.

Explanation:
Given that Mrs. Johnson bought 6 pizzas and she cut them into many equal pieces for the students in her class. Each piece was \(\frac{3}{10}\) of a whole pizza. So the number of students were there in the class is 6 ÷ \(\frac{3}{10}\) which is 6 × \(\frac{10}{3}\)
= 2 × 10
= 20 students.

Divide. Express the quotient in simplest form.

Question 10.
4 ÷ \(\frac{4}{7}\)
Answer:
4 ÷ \(\frac{4}{7}\) = 7.

Explanation:
The division of 4 ÷ \(\frac{4}{7}\) is 4 × \(\frac{7}{4}\) = 7.

Question 11.
6 ÷ \(\frac{2}{7}\)
Answer:
6 ÷ \(\frac{2}{7}\) = 21.

Explanation:
The division of 6 ÷ \(\frac{2}{7}\) is 6 × \(\frac{7}{2}\) which is 3 × 7 = 21.

Question 12.
9 ÷ \(\frac{3}{8}\)
Answer:
9 ÷ \(\frac{3}{8}\) = 24.

Explanation:
The division of 9 ÷ \(\frac{3}{8}\) is 9 × \(\frac{8}{3}\) which is 3 × 8 = 24.

Question 13.
5 ÷ \(\frac{10}{13}\)
Answer:
6\(\frac{1}{2}\).

Explanation:
The division of 5 ÷ \(\frac{10}{13}\) is 5 × \(\frac{13}{10}\) which is \(\frac{13}{2}\) = 6\(\frac{1}{2}\).

Question 14.
10 ÷ \(\frac{5}{14}\)
Answer:
10 ÷ \(\frac{5}{14}\) = 28.

Explanation:
The division of 10 ÷ \(\frac{5}{14}\) is 10 × \(\frac{14}{5}\) which is 2 × 14 = 28.

Question 15.
12 ÷ \(\frac{9}{10}\)
Answer:
12 ÷ \(\frac{9}{10}\) = 13 \(\frac{1}{3}\).

Explanation:
The division of 12 ÷ \(\frac{9}{10}\) is 12 × \(\frac{10}{9}\) which is \(\frac{40}{3}\) = 13 \(\frac{1}{3}\).

Hands-On Activity

Materials:

• 2 paper strips

Use 2 paper strips of the same size and length. Each strip represents 1 whole.

Step 1.
Take 1 paper strip and divide it into halves using vertical lines.
Then find \(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
Refer to your model.
Complete:
There are fourths in a half.

So, \(\frac{1}{2}\) ÷ \(\frac{1}{4}\) =

Step 2.
Find \(\frac{1}{2}\) ÷ \(\frac{1}{4}\) by multiplication.
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\) = Rewrite using the reciprocal of the divisor.
= Multiply.

Step 3.
Divide the other paper strip into one-thirds using vertical lines.
Then find \(\frac{2}{3}\) ÷ \(\frac{1}{6}\).
Refer to your model.
Complete.

Step 4.
Find \(\frac{2}{3}\) ÷ \(\frac{1}{6}\) by multiplication.
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\) = Rewrite using the reciprocal of the divisor
= Multiply.

Hands-On Activity

Dividing Fractions with Remainder

A pitcher contains \(\frac{4}{5}\) quart of orange juice.

Step 1.
Copy the model and divide
Complete: \(\frac{4}{5}\) qt = qt

Step 2.
Use the model to answer this question.
Into how many glasses, each containing \(\frac{3}{10}\) quart, can the orange juice be poured .
How many quarts of orange juice will be left in the pitcher? qt

Step 3.
Now find the number of glasses by division. Express your answer as a mixed number.

The answer 2\(\frac{2}{3}\) means there are 2 glasses of orange juice, each containing \(\frac{3}{10}\) quart, and a remaining glass of orange juice that contains of \(\frac{2}{3}\) of \(\frac{3}{10}\) quart.
How many quarts of orange juice will be left in the pitcher.

Complete.

Question 16.
Adam had \(\frac{5}{7}\) liter of water. He used the water to fill a few glasses completely. The capacity of each glass was \(\frac{2}{7}\) liter. How many glasses of water did Adam fill?

Answer:

Question 17.
Lina had \(\frac{2}{3}\) of a pizza. She cut it into pieces that were each \(\frac{1}{9}\) of the whole pizza. Into how many pieces did she cut it?

Answer:

Divide. Express the quotient in simplest form.

Question 18.
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\)
Answer:
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\)

Explanation:
The simplest form of \(\frac{2}{3}\) ÷ \(\frac{1}{6}\) is \(\frac{2}{3}\) × \(\frac{6}{1}\) = 4.

Question 19.
\(\frac{3}{5}\) ÷ \(\frac{1}{10}\)
Answer:
\(\frac{3}{5}\) ÷ \(\frac{1}{10}\) = 6.

Explanation:
The simplest form of \(\frac{3}{5}\) ÷ \(\frac{1}{10}\) is \(\frac{3}{5}\) × \(\frac{10}{1}\) which is 3 × 2 = 6.

Question 20.
\(\frac{3}{4}\) ÷ \(\frac{1}{2}\)
Answer:
\(\frac{3}{4}\) ÷ \(\frac{1}{2}\) = 1 \(\frac{1}{2}\).

Explanation:
The simplest form of
\(\frac{3}{4}\) ÷ \(\frac{1}{2}\) = \(\frac{3}{4}\) × \(\frac{2}{1}\) which is \(\frac{3}{2}\) = 1 \(\frac{1}{2}\).

Question 21.
\(\frac{1}{6}\) ÷ \(\frac{2}{3}\)
Answer:
\(\frac{1}{6}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{4}\).

Explanation:
The simplest form of
\(\frac{1}{6}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{6}\) × \(\frac{3}{2}\)
= \(\frac{1}{4}\).

Question 22.
\(\frac{5}{8}\) ÷ \(\frac{15}{16}\)
Answer:
\(\frac{5}{8}\) ÷ \(\frac{15}{16}\) = \(\frac{2}{3}\).

Explanation:
The simplest form of
\(\frac{5}{8}\) ÷ \(\frac{15}{16}\) = \(\frac{5}{8}\) × \(\frac{16}{15}\)
= \(\frac{2}{3}\).

Question 23.
\(\frac{7}{16}\) ÷ \(\frac{5}{12}\)
Answer:
\(\frac{7}{16}\) ÷ \(\frac{5}{12}\) = 1\(\frac{1}{20}\).

Explanation:
The simplest form of
\(\frac{7}{16}\) ÷ \(\frac{5}{12}\) = \(\frac{7}{16}\) × \(\frac{12}{5}\)
= \(\frac{21}{20}\)
= 1\(\frac{1}{20}\).

Complete.

Question 24.
Divide \(\frac{5}{9}\) by 4\(\frac{1}{3}\).

Answer:

Caution
Before finding the reciprocal of a whole number or a mixed number, you need to first write ¡t as an improper fraction.

Question 25.
Divide 2\(\frac{3}{5}\) by 1\(\frac{8}{9}\).

2\(\frac{3}{5}\) and 1\(\frac{8}{9}\) are both mixed numbers. Express the mixed numbers as improper fractions.

Answer:

Hands-On Activity

Division Involving Whole Numbers and Fractions

Work in pairs.

Step 1.
Find each quotient.

a) 4 ÷ \(\frac{2}{5}\) and \(\frac{2}{5}\) ÷ 4
Answer:
4 ÷ \(\frac{2}{5}\) = 10.
\(\frac{2}{5}\) ÷ 4 = \(\frac{1}{10}\).

Explanation:
The quotient of 4 ÷ \(\frac{2}{5}\) is
4 ÷ \(\frac{2}{5}\) = 4 × \(\frac{5}{2}\)
= 2 × 5
= 10.
And the quotient of \(\frac{2}{5}\) ÷ 4 is
\(\frac{2}{5}\) ÷ 4 = \(\frac{2}{5}\) × \(\frac{1}{4}\)
= \(\frac{1}{10}\).

b) \(\frac{1}{4}\) ÷ \(\frac{2}{3}\) and \(\frac{2}{3}\) ÷ \(\frac{1}{4}\)
Answer:
\(\frac{1}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{3}{8}\).
\(\frac{2}{3}\) ÷ \(\frac{1}{4}\) = 2 \(\frac{2}{3}\).

Explanation:
The quotient of \(\frac{1}{4}\) ÷ \(\frac{2}{3}\) is
\(\frac{1}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{4}\) × \(\frac{3}{2}\)
= \(\frac{3}{8}\).
The quotient of \(\frac{2}{3}\) ÷ \(\frac{1}{4}\) is
\(\frac{2}{3}\) ÷ \(\frac{1}{4}\) = \(\frac{2}{3}\) × \(\frac{4}{1}\)
= \(\frac{8}{3}\)
= 2 \(\frac{2}{3}\).

c) \(\frac{4}{5}\) ÷ \(\frac{3}{10}\) and \(\frac{3}{10}\) ÷ \(\frac{4}{5}\)
Answer:
\(\frac{4}{5}\) ÷ \(\frac{3}{10}\) = 2\(\frac{2}{3}\).
\(\frac{3}{10}\) ÷ \(\frac{4}{5}\) = \(\frac{3}{8}\).

Explanation:
The quotient of \(\frac{4}{5}\) ÷ \(\frac{3}{10}\) is
\(\frac{4}{5}\) ÷ \(\frac{3}{10}\) = \(\frac{4}{5}\) × \(\frac{10}{3}\)
= \(\frac{8}{3}\)
= 2\(\frac{2}{3}\).
And the quotient of \(\frac{3}{10}\) ÷ \(\frac{4}{5}\) is
\(\frac{3}{10}\) ÷ \(\frac{4}{5}\) = \(\frac{3}{10}\) × \(\frac{5}{4}\)
= \(\frac{3}{8}\).

d) \(\frac{5}{8}\) ÷ \(\frac{3}{4}\) and \(\frac{3}{4}\) ÷ \(\frac{5}{8}\)
Answer:
\(\frac{5}{8}\) ÷ \(\frac{3}{4}\) = \(\frac{5}{6}\).
\(\frac{3}{4}\) ÷ \(\frac{5}{8}\) = 1\(\frac{1}{5}\).

Explanation:
The quotient of \(\frac{5}{8}\) ÷ \(\frac{3}{4}\) is
\(\frac{5}{8}\) ÷ \(\frac{3}{4}\) = \(\frac{5}{8}\) × \(\frac{4}{3}\)
= \(\frac{5}{6}\).
The quotient of \(\frac{3}{4}\) ÷ \(\frac{5}{8}\) is
\(\frac{3}{4}\) ÷ \(\frac{5}{8}\) = \(\frac{3}{4}\) × \(\frac{8}{5}\)
= \(\frac{6}{5}\)
= 1\(\frac{1}{5}\).

Step 2.
What do you observe about the products of each pair of quotients?

Step 3.
Given that \(\frac{6}{7}\) ÷ 9 = \(\frac{2}{21}\) and \(\frac{10}{11}\) ÷ \(\frac{5}{6}\) = \(\frac{12}{11}\), find the following quotients mentally.

a) 9 ÷ \(\frac{6}{7}\)
Answer:
9 ÷ \(\frac{6}{7}\) = 10\(\frac{1}{2}\).

Explanation:
The quotient of 9 ÷ \(\frac{6}{7}\) is
9 ÷ \(\frac{6}{7}\) = 9 × \(\frac{7}{6}\)
= \(\frac{21}{2}\)
= 10\(\frac{1}{2}\).

b) \(\frac{5}{6}\) ÷ \(\frac{10}{11}\)
Answer:
\(\frac{5}{6}\) ÷ \(\frac{10}{11}\) = \(\frac{11}{12}\).

Explanation:
The quotient of \(\frac{5}{6}\) ÷ \(\frac{10}{11}\) is
\(\frac{5}{6}\) ÷ \(\frac{10}{11}\) = \(\frac{5}{6}\) × \(\frac{11}{10}\)
= \(\frac{11}{12}\).

Math Journal Explain in words the meaning of each division statement.

a) 4 ÷ \(\frac{2}{5}\) and \(\frac{2}{5}\) ÷ 4
Answer:
4 ÷ \(\frac{2}{5}\) = 10.
\(\frac{2}{5}\) ÷ 4 = \(\frac{1}{10}\).

Explanation:
The quotient of 4 ÷ \(\frac{2}{5}\) is
4 ÷ \(\frac{2}{5}\) = 4 × \(\frac{5}{2}\)
= 2 × 5
= 10.
And the quotient of \(\frac{2}{5}\) ÷ 4 is
\(\frac{2}{5}\) ÷ 4 = \(\frac{2}{5}\) × \(\frac{1}{4}\)
= \(\frac{1}{10}\).

b) \(\frac{1}{4}\) ÷ \(\frac{2}{3}\) and \(\frac{2}{3}\) ÷ \(\frac{1}{4}\)
Answer:
\(\frac{1}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{3}{8}\).
\(\frac{2}{3}\) ÷ \(\frac{1}{4}\) = 2\(\frac{2}{3}\).

Explanation:
The quotient of \(\frac{1}{4}\) ÷ \(\frac{2}{3}\) is
\(\frac{1}{4}\) ÷ \(\frac{2}{3}\) = \(\frac{1}{4}\) × \(\frac{3}{2}\)
= \(\frac{3}{8}\).
And the quotient of \(\frac{2}{3}\) ÷ \(\frac{1}{4}\) is
\(\frac{2}{3}\) ÷ \(\frac{1}{4}\) = \(\frac{2}{3}\) × \(\frac{4}{1}\)
= \(\frac{8}{3}\)
= 2\(\frac{2}{3}\).

Math in Focus Course 1A Practice 3.1 Answer Key

Divide. Express the quotient ¡n simplest form. Use models to help you.

Question 1.
1 ÷ \(\frac{1}{4}\)

Answer:
1 ÷ \(\frac{1}{4}\) = 4.

Explanation:
The simplest form of 1 ÷ \(\frac{1}{4}\) is
1 ÷ \(\frac{1}{4}\) = 1 × \(\frac{4}{1}\)
= 4.

Question 2.
3 ÷ \(\frac{3}{5}\)

Answer:
3 ÷ \(\frac{3}{5}\) = 5.

Explanation:
The simplest form of 3 ÷ \(\frac{3}{5}\) is
3 ÷ \(\frac{3}{5}\) = 3 × \(\frac{5}{3}\)
= 5.

Question 3.
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\)

Answer:
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\) = 6.

Explanation:
The simplest form of \(\frac{3}{4}\) ÷ \(\frac{1}{8}\) is
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\) = \(\frac{3}{4}\) × \(\frac{8}{1}\)
= 6.

Question 4.
\(\frac{2}{3}\) ÷ \(\frac{2}{9}\)

Answer:
\(\frac{2}{3}\) ÷ \(\frac{2}{9}\) = 3.

Explanation:
The simplest form of \(\frac{2}{3}\) ÷ \(\frac{2}{9}\) is
\(\frac{2}{3}\) ÷ \(\frac{2}{9}\) = \(\frac{2}{3}\) × \(\frac{9}{2}\)
= 3.

Draw a model to find each quotient.

Question 5.
1 ÷ \(\frac{1}{5}\)
Answer:
1 ÷ \(\frac{1}{5}\) = 5.

Explanation:
The quotient of 1 ÷ \(\frac{1}{5}\) is
1 ÷ \(\frac{1}{5}\) = 1 × \(\frac{5}{1}\)
= 5.

Question 6.
4 ÷ \(\frac{8}{9}\)
Answer:
4 ÷ \(\frac{8}{9}\) = 4\(\frac{1}{2}\).

Explanation:
The quotient of 4 ÷ \(\frac{8}{9}\) is
4 ÷ \(\frac{8}{9}\) = 4 × \(\frac{9}{8}\)
= \(\frac{9}{2}\)
= 4\(\frac{1}{2}\).

Question 7.
\(\frac{2}{5}\) ÷ \(\frac{3}{10}\)
Answer:
\(\frac{2}{5}\) ÷ \(\frac{3}{10}\) = 1\(\frac{1}{3}\).

Explanation:
The quotient of \(\frac{2}{5}\) ÷ \(\frac{3}{10}\) is
\(\frac{2}{5}\) ÷ \(\frac{3}{10}\) = \(\frac{2}{5}\) × \(\frac{10}{3}\)
= \(\frac{4}{3}\)
= 1\(\frac{1}{3}\).

Question 8.
\(\frac{3}{4}\) ÷ \(\frac{3}{16}\)
Answer:
\(\frac{3}{4}\) ÷ \(\frac{3}{16}\) = 4.

Explanation:
The quotient of \(\frac{3}{4}\) ÷ \(\frac{3}{16}\) is
\(\frac{3}{4}\) ÷ \(\frac{3}{16}\) = \(\frac{3}{4}\) × \(\frac{16}{3}\)
= 4.

Find each quotient. Express your answer in its simplest form.

Question 9.
4 ÷ \(\frac{1}{7}\)
Answer:
4 ÷ \(\frac{1}{7}\) = 28.

Explanation:
The quotient of 4 ÷ \(\frac{1}{7}\) is
4 ÷ \(\frac{1}{7}\) = 4 × \(\frac{7}{1}\)
= 28.

Question 10.
12 ÷ \(\frac{1}{3}\)
Answer:
12 ÷ \(\frac{1}{3}\) = 36.

Explanation:
The quotient of 12 ÷ \(\frac{1}{3}\) is
12 ÷ \(\frac{1}{3}\) = 12 × \(\frac{3}{1}\)
= 36.

Question 11.
9 ÷ \(\frac{3}{4}\)
Answer:
9 ÷ \(\frac{3}{4}\) = 12.

Explanation:
The quotient of 9 ÷ \(\frac{3}{4}\) is
9 ÷ \(\frac{3}{4}\) = 9 × \(\frac{4}{3}\)
= 3 × 4
= 12.

Question 12.
10 ÷ \(\frac{4}{5}\)
Answer:
10 ÷ \(\frac{4}{5}\) = 12\(\frac{1}{2}\).

Explanation:
The quotient of 10 ÷ \(\frac{4}{5}\) is
10 ÷ \(\frac{4}{5}\) = 10 × \(\frac{5}{4}\)
= \(\frac{25}{2}\)
= 12\(\frac{1}{2}\).

Question 13.
\(\frac{1}{2}\) ÷ \(\frac{1}{8}\)
Answer:
\(\frac{1}{2}\) ÷ \(\frac{1}{8}\) = 4.

Explanation:
The quotient of \(\frac{1}{2}\) ÷ \(\frac{1}{8}\) is
\(\frac{1}{2}\) ÷ \(\frac{1}{8}\) = \(\frac{1}{2}\) × \(\frac{8}{1}\)
= 4.

Question 14.
\(\frac{1}{4}\) ÷ \(\frac{1}{2}\)
Answer:
\(\frac{1}{4}\) ÷ \(\frac{1}{2}\) = \(\frac{1}{2}\).

Explanation:
The quotient of \(\frac{1}{4}\) ÷ \(\frac{1}{2}\) is
\(\frac{1}{4}\) ÷ \(\frac{1}{2}\) = \(\frac{1}{4}\) × \(\frac{2}{1}\)
= \(\frac{1}{2}\).

Question 15.
\(\frac{3}{5}\) ÷ \(\frac{11}{15}\)
Answer:
\(\frac{3}{5}\) ÷ \(\frac{11}{15}\) = 1\(\frac{4}{11}\).

Explanation:
The quotient of \(\frac{3}{5}\) ÷ \(\frac{11}{15}\) is
\(\frac{3}{5}\) ÷ \(\frac{11}{15}\) = \(\frac{3}{5}\) × \(\frac{15}{11}\)
= \(\frac{15}{11}\)
= 1\(\frac{4}{11}\).

Question 16.
\(\frac{2}{3}\) ÷ \(\frac{10}{13}\)
Answer:
\(\frac{2}{3}\) ÷ \(\frac{10}{13}\) = \(\frac{13}{15}\).

Explanation:
The quotient of \(\frac{2}{3}\) ÷ \(\frac{10}{13}\) is
\(\frac{2}{3}\) ÷ \(\frac{10}{13}\) = \(\frac{2}{3}\) × \(\frac{13}{10}\)
= \(\frac{13}{15}\).

Question 17.
\(\frac{5}{6}\) ÷ \(\frac{7}{12}\)
Answer:
\(\frac{5}{6}\) ÷ \(\frac{7}{12}\) = 1\(\frac{3}{7}\).

Explanation:
The quotient of \(\frac{5}{6}\) ÷ \(\frac{7}{12}\) is
\(\frac{5}{6}\) ÷ \(\frac{7}{12}\) = \(\frac{5}{6}\) × \(\frac{12}{7}\)
= \(\frac{10}{7}\)
= 1\(\frac{3}{7}\).

Question 18.
\(\frac{3}{4}\) ÷ \(\frac{9}{16}\)
Answer:
\(\frac{3}{4}\) ÷ \(\frac{9}{16}\) = 1\(\frac{1}{3}\).

Explanation:
The quotient of \(\frac{3}{4}\) ÷ \(\frac{9}{16}\) is
\(\frac{3}{4}\) ÷ \(\frac{9}{16}\) = \(\frac{3}{4}\) × \(\frac{16}{9}\)
= \(\frac{4}{3}\)
= 1\(\frac{1}{3}\).

Find each quotient. Express your answer in its simplest form.

Question 19.
\(\frac{1}{3}\) ÷ \(\frac{7}{4}\)
Answer:
\(\frac{1}{3}\) ÷ \(\frac{7}{4}\) = \(\frac{4}{21}\).

Explanation:
The quotient of \(\frac{1}{3}\) ÷ \(\frac{7}{4}\) is
\(\frac{1}{3}\) ÷ \(\frac{7}{4}\) = \(\frac{1}{3}\) × \(\frac{4}{7}\)
= \(\frac{4}{21}\).

Question 20.
\(\frac{1}{2}\) ÷ \(\frac{8}{4}\)
Answer:
\(\frac{1}{2}\) ÷ \(\frac{8}{4}\) = \(\frac{1}{4}\).

Explanation:
The quotient of \(\frac{1}{2}\) ÷ \(\frac{8}{4}\) is
\(\frac{1}{2}\) ÷ \(\frac{8}{4}\) = \(\frac{1}{2}\) × \(\frac{4}{8}\)
= \(\frac{1}{4}\).

Question 21.
\(\frac{1}{9}\) ÷ \(\frac{14}{3}\)
Answer:
\(\frac{1}{9}\) ÷ \(\frac{14}{3}\) = \(\frac{1}{42}\).

Explanation:
The quotient of \(\frac{1}{9}\) ÷ \(\frac{14}{3}\) is
\(\frac{1}{9}\) ÷ \(\frac{14}{3}\) = \(\frac{1}{9}\) × \(\frac{3}{14}\)
= \(\frac{1}{42}\).

Question 22.
\(\frac{5}{8}\) ÷ \(\frac{21}{4}\)
Answer:
\(\frac{5}{8}\) ÷ \(\frac{21}{4}\) = \(\frac{5}{42}\).

Explanation:
The quotient of \(\frac{5}{8}\) ÷ \(\frac{21}{4}\) is
\(\frac{5}{8}\) ÷ \(\frac{21}{4}\) = \(\frac{5}{8}\) × \(\frac{4}{21}\)
= \(\frac{5}{42}\).

Question 23.
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{8}\)
Answer:
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{8}\) = 1 \(\frac{11}{17}\).

Explanation:
The quotient of 3\(\frac{1}{2}\) ÷ 2\(\frac{1}{8}\) is
3\(\frac{1}{2}\) ÷ 2\(\frac{1}{8}\) = \(\frac{7}{2}\) ÷ \(\frac{17}{8}\)
= \(\frac{7}{2}\) × \(\frac{8}{17}\)
= \(\frac{28}{17}\)
= 1 \(\frac{11}{17}\).

Question 24.
5\(\frac{1}{4}\) ÷ 3\(\frac{1}{2}\)
Answer:
5\(\frac{1}{4}\) ÷ 3\(\frac{1}{2}\) = \(\frac{3}{2}\).

Explanation:
The quotient of 5\(\frac{1}{4}\) ÷ 3\(\frac{1}{2}\) is
5\(\frac{1}{4}\) ÷ 3\(\frac{1}{2}\) = \(\frac{21}{4}\) ÷ \(\frac{7}{2}\)
= \(\frac{21}{4}\) × \(\frac{2}{7}\)
= \(\frac{3}{2}\).

Question 25.
7\(\frac{3}{5}\) ÷ 8\(\frac{11}{15}\)
Answer:
7\(\frac{3}{5}\) ÷ 8\(\frac{11}{15}\) = \(\frac{114}{131}\).

Explanation:
The quotient of 7\(\frac{3}{5}\) ÷ 8\(\frac{11}{15}\) is
7\(\frac{3}{5}\) ÷ 8\(\frac{11}{15}\) =\(\frac{38}{5}\) ÷ \(\frac{131}{15}\)
= \(\frac{38}{5}\) × \(\frac{15}{131}\)
= \(\frac{114}{131}\).

Question 26.
12\(\frac{2}{3}\) ÷ 5\(\frac{11}{13}\)
Answer:
12\(\frac{2}{3}\) ÷ 5\(\frac{11}{13}\) = 2\(\frac{1}{6}\).

Explanation:
The quotient of 12\(\frac{2}{3}\) ÷ 5\(\frac{11}{13}\) is
12\(\frac{2}{3}\) ÷ 5\(\frac{11}{13}\) = \(\frac{26}{3}\) ÷ \(\frac{76}{13}\)
= \(\frac{38}{3}\) × \(\frac{13}{76}\)
= \(\frac{13}{6}\)
= 2\(\frac{1}{6}\).

Solve. Show your work.

Question 27.
6 pizzas were shared equally among a group of children. Each child got \(\frac{1}{9}\) of a pizza. How many children were in the group?
Answer:
The number of children were in the group is 54 children.

Explanation:
Given that 6 pizzas were shared equally among a group of children and each child got \(\frac{1}{9}\) of a pizza. So the number of children were in the group is 6 ÷ \(\frac{1}{9}\)
= 6 × 9
= 54 children.

Question 28.
A rectangle has an area of 15 square meters. It ¡s divided into parts, each with an area of \(\frac{3}{8}\) square meter. Into how many parts has the rectangle been divided?
Answer:
The number of parts has the rectangle been divided is 40 square meters.

Explanation:
Given that a rectangle has an area of 15 square meters and it ¡s divided into parts, each with an area of \(\frac{3}{8}\) square meter. So the number of parts has the rectangle been divided is 15 ÷ \(\frac{3}{8}\)
= 15 × \(\frac{8}{3}\)
= 5 × 8
= 40 square meters.

Question 29.
How many \(\frac{3}{8}\)-cup servings are in a pitcher containing 6\(\frac{3}{4}\) cups of orange juice?
Answer:
The number of serving pitchers be 18 cups.

Explanation:
Given that 1 cup contains \(\frac{3}{8}\) servings are in a pitcher containing and the total is 6\(\frac{3}{4}\) which is \(\frac{27}{4}\). So the number of serving pitchers be \(\frac{27}{4}\) ÷ \(\frac{3}{8}\)
= \(\frac{27}{4}\) × \(\frac{8}{3}\)
= 9 × 2
= 18 cups.

Question 30.
Maria buys 8\(\frac{1}{3}\) pounds of beef to make tacos for a party. She uses \(\frac{5}{9}\) pound of beef for each taco. How many tacos can Maria make?
Answer:
The number of tacos can Maria make is 15 tacos.

Explanation:
Given that Maria buys 8\(\frac{1}{3}\) pounds of beef to make tacos for a party which is \(\frac{25}{3}\) and she uses \(\frac{5}{9}\) pound of beef for each taco. So the number of tacos can Maria make is \(\frac{25}{3}\) ÷ \(\frac{5}{9}\)
= \(\frac{25}{3}\) × \(\frac{9}{5}\)
= 5 × 3
= 15.

The capacity of a large milk carton is 1\(\frac{1}{2}\) liters. A dozen large cartons are poured into a container and then poured into small cartons that each hold \(\frac{3}{10}\) liter. How many small cartons of milk can be filled?
Answer:
The number of small cartons of milk that can be filled is 60 cartons.

Explanation:
Given that the capacity of a large milk carton is 1\(\frac{1}{2}\) liters which is \(\frac{3}{2}\), so in pounds, it will be 12 × \(\frac{3}{2}\)
= 6 × 3
= 18.
And a dozen large cartons are poured into a container and then poured into small cartons that each hold \(\frac{3}{10}\) liter. Here, the total number of small cartons of milk can be filled = Total number of pounds of a dozen large cartons ÷ small carton capacity which is
= 18 ÷ \(\frac{3}{10}\)
= 18 × \(\frac{10}{3}\)
= 6 × 10
= 60.
The number of small cartons of milk that can be filled is 60 cartons.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Multiplying and Dividing Fractions and Decimals to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Answer Key Multiplying and Dividing Fractions and Decimals

Math in Focus Grade 6 Chapter 3 Quick Check Answer Key

Add or subtract.

Question 1.
5.3 + 6.49
Answer:
5.3 + 6.49 = 11.79.

Explanation:
The addition of 5.3 and 6.49 is 11.79.

Question 2.
6.51 – 2.03
Answer:
6.51 – 2.03 = 4.48.

Explanation:
The subtraction of 6.51 and 2.03 is 4.48.

Question 3.
9.62 + 7.08
Answer:
9.62 + 7.08 = 16.7.

Explanation:
The addition of 9.62 and 7.08 is 16.7.

Question 4.
8.4 – 7.52
Answer:
8.4 – 7.52 = 0.88.

Explanation:
The subtraction of 8.4 and 7.52 is 0.88.

Express each improper fraction as a mixed number in simplest form.

Question 5.
\(\frac{19}{3}\)
Answer:
6\(\frac{1}{3}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 6\(\frac{1}{3}\).

Question 6.
\(\frac{26}{4}\)
Answer:
6\(\frac{1}{2}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 6\(\frac{1}{2}\).

Question 7.
\(\frac{30}{7}\)
Answer:
4\(\frac{2}{7}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 4\(\frac{2}{7}\).

Question 8.
\(\frac{38}{5}\)
Answer:
7\(\frac{3}{5}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 7\(\frac{3}{5}\).

Question 9.
\(\frac{50}{8}\)
Answer:
6\(\frac{1}{4}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 6\(\frac{1}{4}\).

Question 10.
\(\frac{69}{9}\)
Answer:
7\(\frac{2}{3}\).

Explanation:
Here, improper fraction is a fraction in which the numerator is greater than the denominator. So the mixed fraction will be 7\(\frac{2}{3}\).

Express each mixed number as an improper fraction.

Question 11.
3\(\frac{1}{4}\)
Answer:
\(\frac{13}{4}\).

Explanation:
Here, a mixed fraction is a whole number and a proper fraction represented fraction. So 3\(\frac{1}{4}\) is \(\frac{13}{4}\).

Question 12.
4\(\frac{3}{7}\)
Answer:
\(\frac{31}{7}\).

Explanation:
Here, a mixed fraction is a whole number and a proper fraction represented fraction. So 4\(\frac{3}{7}\) is \(\frac{31}{7}\).

Question 13.
8\(\frac{5}{9}\)
Answer:
\(\frac{77}{9}\).

Explanation:
Here, a mixed fraction is a whole number and a proper fraction represented fraction. So 8\(\frac{5}{9}\) is \(\frac{77}{9}\).

Find each product in simplest form.

Question 14.
\(\frac{2}{5}\) × \(\frac{7}{8}\)
Answer:
\(\frac{2}{5}\) × \(\frac{7}{8}\) = \(\frac{7}{20}\).

Explanation:
The product of \(\frac{2}{5}\) × \(\frac{7}{8}\) is \(\frac{7}{20}\).

Question 15.
\(\frac{10}{11}\) × \(\frac{33}{5}\)
Answer:
\(\frac{10}{11}\) × \(\frac{33}{5}\) = 6.

Explanation:
The product of \(\frac{10}{11}\) × \(\frac{33}{5}\) is 2×3 = 6.

Question 16.
\(\frac{8}{7}\) × \(\frac{35}{12}\)
Answer:
\(\frac{8}{7}\) × \(\frac{35}{12}\) = 2\(\frac{1}{2}\).

Explanation:
The product of \(\frac{8}{7}\) × \(\frac{35}{12}\) which is \(\frac{10}{4}\) = 2\(\frac{1}{2}\).

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 2 Negative Numbers and the Number Line to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 2 Answer Key Negative Numbers and the Number Line

Math in Focus Grade 6 Chapter 2 Quick Check Answer Key

Draw a horizontal number line to represent each set of numbers.

Question 1.
Odd numbers from 20 to 30
Answer:
Odd numbers from 20 to 30 are 21, 23, 25, 27, 29.

Explanation:
Odd numbers from 20 to 30 are 21, 23, 25, 27, 29 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Question 2.
Mixed numbers from 3 to 5, with an interval of \(\frac{1}{6}\) between each pair of mixed numbers
Answer:
Mixed numbers from 3 to 5, with an interval of \(\frac{1}{6}\) between each pair of mixed numbers are 3, 3(1/6), 3(2/6), 3(3/6), 3(4/6), 3(5/6), 4, 4(1/6), 4(2/6), 4(3/6), 4(4/6), 4(5/6), 5.

Question 3.
Decimals between 8.0 and 10.0, with an interval of 0.25 between each pair of decimals
Answer:

Explanation:
Decimals between 8.0 and 10.0, with an interval of 0.25 between each pair of decimals8.25, 8.5, 8.75, 9, 9.25, 9.5, 9.75 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Compare each pair of numbers using > or <. Use a number line to help you.

Question 4.

Answer:


Explanation:
The given numbers are 3/8 and 5/6. Here we have to compare the pair of numbers. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left as we can observe in the above image. After comparing numbers on the number line 3/8 is less than 5/6.

Question 5.

Answer:


Explanation:
The given decimal numbers are 2.14 and 2.104. Here we have to compare the pair of numbers. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left as we can observe in the above image. After comparing decimal numbers on the number line 2.14 is greater than 2.104.

Question 6.

Answer:


Explanation:
The given numbers are 0.72 and 7/12. Here we have to compare the pair of numbers. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left as we can observe in the above image. After comparing numbers on the number line 0.72 is greater than 7/12.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Review Test to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Review Test Answer Key

Concepts and Skills

Draw a horizontal number line to represent each set of numbers.

Question 1.
Positive whole numbers less than 8
Answer:
0, 1, 2, 3, 4, 5, 6 and 7.

Explanation:
The positive whole numbers less than 8 are 0, 1, 2, 3, 4, 5, 6 and 7.

Question 2.
Whole numbers greater than 25 but less than 33
Answer:
26, 27, 28, 29, 30, 31 and 32.

Explanation:
The whole numbers greater than 25 and less than 33 are 26, 27, 28, 29, 30, 31 and 32.

Question 3.
Mixed numbers from 4 to 6, with an interval of \(\frac{1}{4}\) between each pair of mixed numbers
Answer:
4\(\frac{1}{4}\) , 4\(\frac{2}{4}\) , 4\(\frac{3}{4}\) ,  5\(\frac{1}{4}\) , 5\(\frac{2}{4}\) and 5\(\frac{3}{4}\) .

Explanation:
The mixed numbers numbers from 4 to 6 are 4\(\frac{1}{4}\) , 4\(\frac{2}{4}\) , 4\(\frac{3}{4}\) ,  5\(\frac{1}{4}\) , 5\(\frac{2}{4}\) and 5\(\frac{3}{4}\) .

Question 4.
Decimals between 3.0 and 3.8, with an interval of 0.2 between each pair of decimals
Answer:
3.2, 3.4 and 3.6.

Explanation:
Decimals between 3.0 and 3.8 with 0.2 interval are 3.2, 3.4 and 3.6.

Express each number as a product of its prime factors.

Question 5.
42
Answer:
2 x 3 x 7

Explanation:
Prime factors of 42 are 2, 3 and 7
The product of prime factors of 42 is 2 x 3 x 7.

Question 6.
150
Answer:
2 x 3 x 5 x 5

Explanation:
Prime factors of 150 are 2, 3 and 5
The product of prime factors of 150 is 2 x 3 x 5 x 5.

Find the common factors of each pair of numbers.

Question 7.
21 and 63
Answer:
1, 3, 7, 21.

Explanation:
Factors of 21 – 1, 3, 7, 21
Factors of 63 – 1, 3, 7, 9, 21, 63.
Common factors of 21 and 63 are 1, 3, 7, and 21.

Question 8.
35 and 70
Answer:
1, 5, 7, 35.

Explanation:
Factors of 35 are 1, 5, 7, 35
Factors of 70 are 1, 2, 5, 7, 10, 14,  35, 70.
Common factors of 35 and 70 are 1, 5, 7 and 35.

Find the greatest common factor of each pair of numbers.

Question 9.
8 and 12
Answer:
4

Explanation:
Factors of 8 are 1, 2, 4, 8
Factors of 12 are 1, 2, 3, 4, 6, 12
The greatest common factor of 8 and 12 is 4.

Question 10.
42 and 32
Answer:
2

Explanation:
Factors of 42 are 1, 2, 3, 6, 7, 14, 21, 42
Factors of 32 are 1, 2, 4, 8, 16, 32
The greatest common factor of 42 and 32 is 2.

Find the first three common multiples of each pair of numbers.

Question 11.
4 and 5
Answer:
20, 40, 60.

Explanation:
Multiples of 4 -4,8,12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60
Multiples of 5 – 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60
First three common multiples of 4 and 5 are 20, 40, 60.

Question 12.
9 and 21
Answer:
63, 126 and 189.

Explanation:
Multiples of 9 -9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126.
Multiples of 21 -21, 42, 63, 84, 105, 126, 147, 168, 189
First three common multiples of 9 and 21 are 63, 126, 189.

Find the least common multiple of each pair of numbers.

Question 13.
6 and 15
Answer:
30

Explanation:
Multiples of 6 -6, 12, 18, 24, 30
Multiples of 15 – 15, 30, 45.
Least common multiple of 6 and 15 is 30.

Question 14.
8 and 11
Answer:
88

Explanation:
Multiples of 8 – 8, 16, 24, 36, 40, 48, 56, 64, 72, 80, 88.
Multiples of 11 – 11, 22, 33, 44, 55, 66, 77, 88, 99,
Least common multiple of 8 and 11 is 88.

Find the square of each number.

Question 15.
14
Answer:

196

Explanation:
14² = 14 x 14
=196
The square of 14 is 196.

Question 16.
30
Answer:

900

Explanation:
30² = 30 x 30
= 900
The square of 30 is 900.

Find the square root of each number.

Question 17.
169
Answer:
13

Explanation:
Recalling the multiplication facts of 169, you know that
169 = 13 x 13
= 13²
So, \(\sqrt{169}\) = 13

Question 18.
484
Answer:
22

Explanation:
Recalling the multiplication facts of 484, you know that
484 = 22 x 22
= 22²
So, \(\sqrt{484}\) = 22

Find the cube of each number.

Question 19.
4
Answer:
64

Explanation:
4³ = 4 x 4 x 4
= 16 x 4
= 64
The cube of the number 4 is 64.

Question 20.
20
Answer:
8000

Explanation:
20³ = 20 x 20 x 20
= 400 x 20
= 8000
The cube of the number 20 is 8000.

Find the cube root of each number.

Question 21.
1,331
Answer:
11

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 1331 = 11 x 11 x 11
=11³
so, cube root of 1331 is 11.

Question 22.
9,261
Answer:
21

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 9261 = 21 x 21 x 21
=21³
so, cube root of 9621 is 21.

Find the value of each of the following.

Question 23.
4³ + 6²
Answer:
100

Explanation:
4³ = 4 x 4 x 4 = 64
6² = 6 x 6 = 36
4³ + 6² = 64 + 36 = 100
4³ + 6²  = 100

Question 24.
8³ – 5²
Answer:
487

Explanation:
8³ = 8 x 8 x 8 = 512
5² = 5 x 5 = 25
8³ – 5² = 512 – 25 = 487
8³ – 5² = 487

Question 25.
5³ × 4³ – 13²
Answer:
7381

Explanation:
5³ = 5 x 5 x 5 = 125
4³ = 4 x 4 x 4= 64
13² = 169
5³ x 4³ – 13² =125 x 64 – 169 = 7381
5³ x 4³ – 13² = 7381

Question 26.
8² + 10³ ÷ 5²
Answer:
104

Explanation:
8² = 8 x 8 = 64
10³ = 10 x 10 x 10 = 1000
5² = 5 x 5 = 25
8² + 10³ ÷  5² = 64 + (1000 ÷ 25)
= 64 + 40
= 104
8² + 10³ ÷  5² = 104.

Solve.

Question 27.
Given that 63² = 3,969, find the square of 630.
Answer:
396900

Explanation:
If 63² = 3,969 then square of 630 will be 396900.

Question 28.
Given that \(\sqrt{1,225}\) = 35, evaluate 350²
Answer:
122500

Explanation:
If \(\sqrt{1,225}\) = 35 then 350² will be 122500.

Question 29.
Given that 16³ = 4,096, find the cube root of 4,096,000.
Answer:
160

Explanation:
If 16³ = 4,096 then cube root of 4,096,000will be 160.

Question 30.
Given that = 24, evaluate 240³.
Answer:
13824000

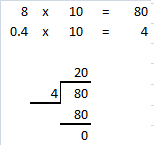
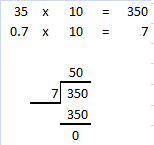
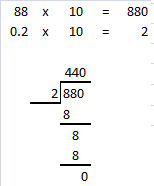
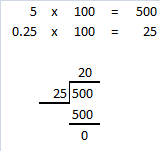
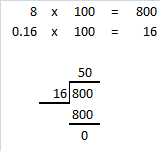
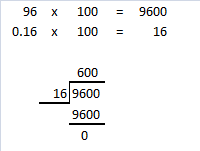
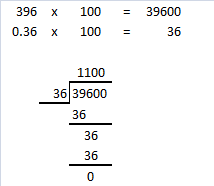
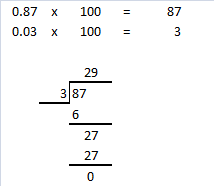
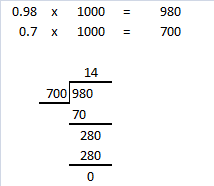
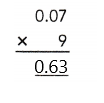
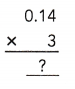
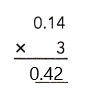
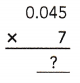
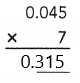
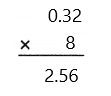
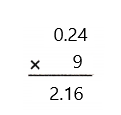
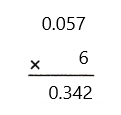
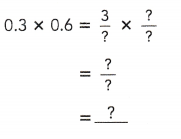
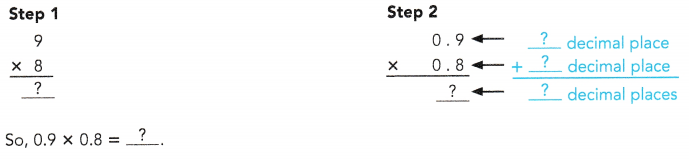
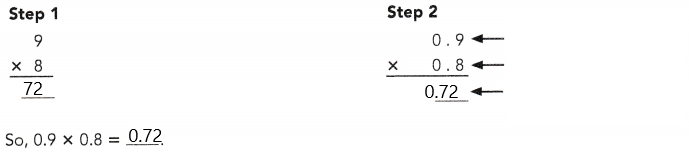
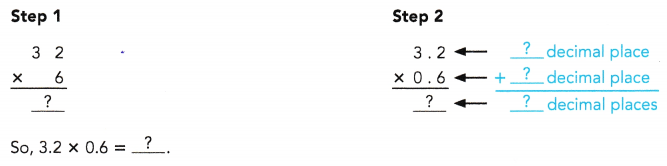
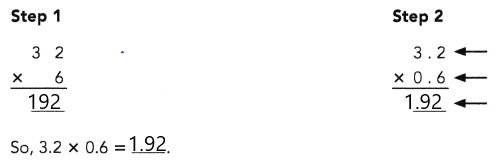
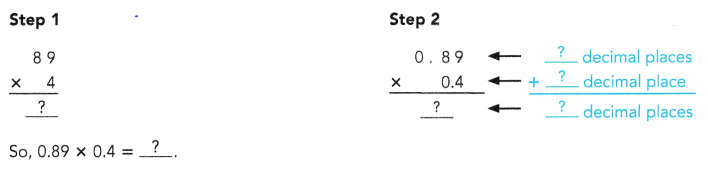
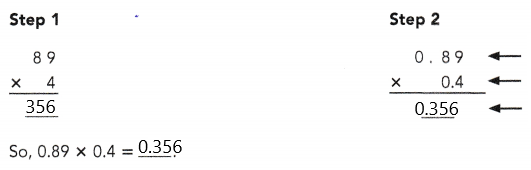
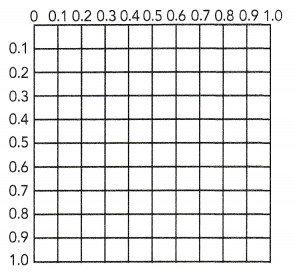
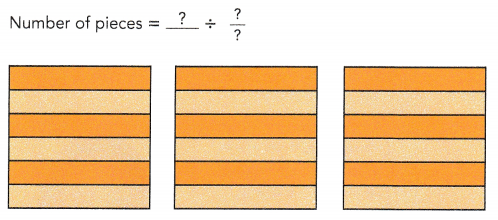
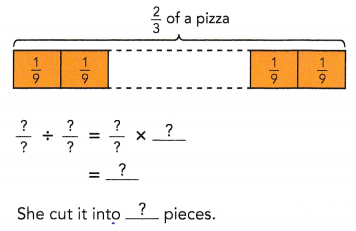
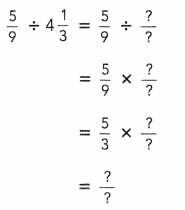
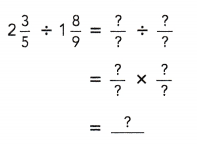
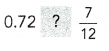
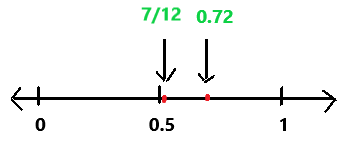
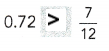
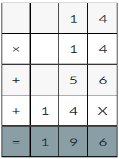
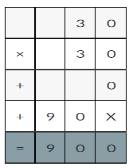
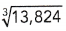If = 24 then 240³ will be 13824000.

Problem Solving

Solve. Show your work.

Question 31.
Find two consecutive numbers whose squares differ by 25.
Answer:
12 and 13

Explanation:
Square of 12 is 144, square of 13 is 169
169 – 144 = 25
SO, 12 and 13 are the two consecutive numbers whose squares differ by 25.

Question 32.
Riley is packing 144 pencils, 120 files, and 108 notebooks equally into as many boxes as possible.
a) Find the greatest number of boxes that Riley could pack the items into.
Answer:
9 boxes

Explanation:
Riley is packing 144 pencils, 120 files, and 108 notebooks equally into as many boxes as possible.
He needs 12 of each thing and he can pack 9 boxes.(12 x 9 = 108).

b) Find the number of pencils, files, and notebooks in each box.
Answer:
12 pencils, 12 files and 12 notebooks.

Question 33.
Imelda, Susan, and Clara are driving go-carts around a track. Imelda takes 14 minutes, Susan takes 18 minutes, and Clara takes 10 minutes to drive one lap. Suppose all three of them start together at a point and drive at their same speeds. After how many minutes would all three meet again?
Answer:

Question 34.
How many squares with sides that are 6 inches long are needed to cover a square with a side length of 30 inches without overlapping?
Answer:
5

Explanation:
A  square with a side 6 inches long,
6 x 5 = 30
So, to cover a square with a side length of 30 inches 5 squares with side of 6 inches are needed.

Question 35.
A wooden crate is a cube with edge lengths of 18 inches. The crate contains tiny plastic cubes with edge lengths of 3 inches. How many plastic cubes can fit inside the wooden crate?
Answer:
6

Explanation:
A wooden crate is a cube with edge lengths of 18 inches.
The crate contains tiny plastic cubes with edge lengths of 3 inches
3 x 6 = 18
So, 6 plastic cubes can fit inside the wooden crate.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.3 Common Factors and Multiples to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.3 Answer Key Common Factors and Multiples

Math in Focus Grade 6 Chapter 1 Lesson 1.3 Guided Practice Answer Key

Complete.

Use the lists of factors on the right to find the common factors of 10 and 28.

Question 1.
The factors of 1o are , , , and .
The factors of 28 are , , , , and .
The common factors of 10 and 28 are and .

Answer:
The factors of 10are 1, 2, 5, 10
The factors of 28 are 1, 2, 4, 7, 4, 28
The common factors are 1 and 2.

Find the common factors of each pair of numbers.

Question 2.
16 and 24
Answer:
1, 2 and 4.

Explanation:
The factors of 16 are 1, 2, 4, 8, 16
The factors of 24 are 1, 2, 3, 4, 6, 12, 24
The common factors of 16 and 24 are 1, 2 and 4.

Question 3.
27 and 35
Answer:
1

Explanation:
The factors of 27 are 1, 3, 9, 27
The factors of 35 are 1, 5, 7, 35
The common factors of 27 and 35 is 1.

Question 4.
36 and 50
Answer:
1 and 2.

Explanation:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
The factors of 50 are 1, 2, 5, 10, 25, 50
The common factors of 36 and 50 are 1 and 2.

Question 5.
40 and 54
Answer:
1 and 2.

Explanation:
The factors of 40 are 1, 2, 4, 5, 8, 10, 20, 40
The factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54.
The common factors of 40 and 54 are 1 and 2.

Complete.

Question 6.
Find the greatest common factor of 20 and 32.
Answer:
Method 1

The factors of 20 are , , , , , and .
The factors of 32 are , , , , , and
The common factors of 20 and 32 are , , and .
The greatest common factor of 20 and 32 is .

Method 2
By prime factorization,
20 = 2 • •
32 = 2 • • • •
Greatest common factor = 2 •
=
The greatest common factor of 20 and 32 is .

Method 3

The greatest common factor of 20 and 32 is .

Find the greatest common factor of each pair of numbers.

Question 7.
15 and 27
Answer:
3

Explanation:
The factors of 15 = 1, 3, 5, 15
The factors of 27 = 1, 3, 9, 27
The common factors of 15 and  27 are 1 and 3
The greatest common factor of 15 and 27 is 3.

Question 8.
36 and 54
Answer:
18

Explanation:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
The factors of 54 are  1, 2, 3, 6, 9, 18, 27, 54
The common factors of 36 and 54 are 1, 3, 6, 9, 18
The greatest common factor of 36 and 54 is 18.

Question 9.
48 and 72
Answer:
24

Explanation:
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 72 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 36, 72
The common factors of 48 and 72 are 1, 2, 3, 4, 6, 8, 12, 16, 24
The greatest common factor of 48 and 72 is 24.

Question 10.
40 and 100
Answer:
20

Explanation:
The factors of 40 are 1, 2, 4, 5, 8, 10, 20, 40
The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100
The common factors of 40 and 100 are 1, 2, 4, 5, 10, 20.
The greatest common factors of 40 and 100 is 20.

Hands-On Activity

Find The Common Factors And The Greatest Common Factor Of Two Numbers

Materials:

• number cards (from 10 to 100)
• factor cards (2s, 3s, 5s, and 7s)

Work in pairs.

Step 1.
Shuffle the number cards and place them face down on a flat surface. Give half the factor cards to each player.

Step 2.
Each player turns over a number card and uses his or her factor cards to show the prime factorization of the number.

Step 3.
The first player states the greatest common factor (GCF) of the two numbers. If the player is correct, the player keeps the two number cards. Players reuse the factor cards on each turn.
Example

Step 4.
Two new number cards are turned over and the process repeats. This time the second player gets to state the GCF.
Step 5.
Play continues until all number cards have been used. The player with more number cards is the winner.

Use the greatest common factor with the distributive property.

Express 12 + 20 as a product of the greatest common factor of the numbers and another sum.

First find the greatest common factor of the two numbers.

Greatest common factor of 12 and 20 = 2 • 2
= 4
Then write the sum a different way. You know that
12 = 4 • 3 20 = 4 • 5
So, 12 + 20 = 4 • 3 + 4 • 5
= 4(3 + 5)
The distributive property says that:
4(3 + 5) = 4 • 3 + 4 • 5

The number lines below show you that 12 + 20 and 4(3 + 5) represent the same number.
Notice that either way, you “end up” at the same place on the number line.
12 + 20 is a jump of 12 plus a jump of 20.

Complete.

Question 11.
Express 18 + 45 as a product of the greatest common factor of the numbers and another sum.
By prime factorization,
18 = 2 • • 45 = 3 • •
Greatest common factor of 18 and 45 = •
=
18 + 45 = • + •
= ( + )
Answer:

Express the sum of each pair of numbers as a product of the greatest common factor of the numbers and another sum.

Question 12.
35 + 91
Answer:
7( 5 + 13 )

Explanation:
By prime factorization,
35 = 5 x 7, 91 = 7 x 13
Greatest common factor of 35 and 91 = 7
35 + 91 = 5 . 7 + 13 . 7
= 7(5+ 13)
35 + 91 = 7(5 + 13).

Question 13.
60 + 85
Answer:
5 ( 12 + 17 )

Explanation:
By prime factorization,
60 = 2 x 2 x 3 x 5, 85 = 5 x 17
Greatest common factor of 60and 85 = 5
60 + 85 = 5 . 12 + 5 . 17
= 5( 12 + 17 )
60 + 85 = 5( 12 + 17 ).

Question 14.
24 + 64
Answer:
8( 3 + 8 )

Explanation:
By prime factorization,
24 = 2 x 2 x 2 x 3, 64 = 2 x 2 x 2 x 2 x 2 x 2
Greatest common factor of 2 4and 64 = 2 . 2 . 2 = 8
24 + 64 = 8 . 3 + 8 . 8
= 8( 3 + 8)
24 + 64 = 8( 3 + 8 )

Complete.

Question 15.

Answer:
15, 30 and 45

Explanation:
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45
The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45
The first three common multiples of 3 and 5 are 15, 30, 45.

List the first ten multiples of each pair of numbers. Then find the common multiples of each pair of numbers from the first ten multiples.

Question 16.
6 and 12
Answer:
12, 24, 36 and 48.

Explanation:
The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
The common multiples of 6 and 12 from first ten multiples are 12, 24, 36, 48.

Question 17.
7 and 11
Answer:
11

Explanation:
The multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77
The multiples of 11 are 11, 22, 33, 44, 55, 66, 77, 88, 99, 110.
The common multiples of 7 and 11 from first ten multiples is 77.

Complete.

Question 18.
Find the least common multiple of 8 and 10.
Method 1

Method 2
By prime factorization,
8 = 2 • • 10 = 2 •
Least common multiple = 2 • • •
=
The least common multiple of 8 and 10 is .

Method 3

The least common multiple of 8 and 10 is .

Find the least common multiple of each pair of numbers.

Question 19.
3 and 7
Answer:
21

Explanation:
By prime factorization,
3 = 3, 7= 7
The least common multiple = 3 . 7 = 21
The least common multiple of 3 and 7 is 21.

Question 20.
5 and 12
Answer:
60

Explanation:
By prime factorization,
5 = 5, 12 = 2 x 2 x 3
The least common multiple = 2 . 2 . 2. 3 . 5 = 60
The least common multiple of 5 and 12 is 60

Question 21.
4 and 9
Answer:
36

Explanation:
By prime factorization,
4 = 2 x 2, 9 = 3 x 3
The least common multiple = 2 . 2 . 3 . 3 = 36
The least common multiple of 4 and 9 is 36

Question 22.
6 and 11
Answer:
66

Explanation:
By prime factorization,
6 = 2 x 3, 11 = 11
The least common multiple = 2 . 3 . 11 = 66
The least common multiple of 6 and 11 is 66.

Math in Focus Course 1A Practice 1.3 Answer Key

Find the common factors of each pair of numbers.

Question 1.
18 and 63
Answer:
1, 3 and 9

Explanation:
The factors of 18 are 1, 2, 3, 6, 9, 18
The factors of 63 are 1, 3, 7, 9, 21, 63
The common factors of 18 and 63 are 1, 3, 9.

Question 2.
15 and 75
Answer:
1, 3, 5 and 15.

Explanation:
The factors of 15 are 1, 3, 5, 15
The factors of 75 are 1, 3, 5, 15, 25, 75
The common factors of 15 and 75 are 1, 3, 5, 15.

Question 3.
30 and 50
Answer:
1, 2, 5 and 10

Explanation:
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
The factors of 50 are 1, 2, 5, 10, 25, 50
The common factors of 30 and 500 are 1, 2, 5, 10.

Question 4.
64 and 92
Answer:
1, 2 and 4.

Explanation:
The factors of 64 are 1, 2, 4, 8, 16, 32, 64
The factors of 92 are 1, 2, 4, 23, 46, 92
The common factors of 44 and 92 are 1, 2, 4.

Question 5.
26 and 78
Answer:
1, 2, 13 and 26.

Explanation:
The factors of 26 are 1, 2, 13, 26
The factors of 78 are 1, 2, 6, 13, 26, 39, 78
The common factors of 26 and 78 are 1, 2, 13, 26.

Question 6.
55 and 88
Answer:
1 and 11.

Explanation:
The factors of 55 are 1, 5, 11, 55
The factors of 88 are 1, 2, 4, 8, 11, 22, 44, 88
The common factors of 55 and 88 are 1, 11.

Find the greatest common factor of each pair of numbers.

Question 7.
24 and 36
Answer:
12

Explanation:
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
The common factors are 1, 2, 3, 4, 6, 12
The greatest common factors of 24 and 36 is 12.

Question 8.
30 and 54
Answer:
6

Explanation:
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
The factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54
The common factors are 1, 2, 3, 6
The greatest common factors of 30 and 54 is 6.

Question 9.
42 and 98
Answer:
14

Explanation:
The factors of 42 are 1, 2, 3, 6, 7, 14, 21, 42
The factors of 98 are 1, 2, 7, 14, 49, 98
The common factors are 1, 2, 7, 14
The greatest common factors of 42 and 98 is 14.

Question 10.
48 and 72
Answer:
24

Explanation:
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The common factors are 1, 2, 3, 4, 6, 8, 12, 24
The greatest common factors of 48 and 72 is 24.

Question 11.
65 and 91
Answer:
13

Explanation:
The factors of 65 are 1, 5, 13, 65
The factors of 91 are 1, 7, 13, 91
The common factors are 1, 13
The greatest common factors of 65 and 91 is 13.

Question 12.
84 and 100
Answer:
4

Explanation:
The factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100
The common factors are 1, 2, 4
The greatest common factors of 84 and 100 is 4.

Find the first five common multiples of each pair of numbers.

Question 13.
5 and 6
Answer:
30, 60, 90, 120 and 150

Explanation:
The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65…..
The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60….
First five common multiples of 5 and 6 are 30, 60, 90, 120, 150.

Question 14.
4 and 7
Answer:
28, 56, 84, 112, 140

Explanation:
The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60….
The multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70…..
First five common multiples of 4 and 7 are 28, 56, 84, 112 and 140

Question 15.
9 and 10
Answer:
90, 180, 270, 360 and 450.

Explanation:
The multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90…..
The multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80 , 90…..
First five common multiples of 10 and 9 are 90, 180, 270, 360, 450.

Question 16.
8 and 11
Answer:
88, 176, 264, 352 and 440.

Explanation:
The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88…
The multiples of 11 are 11, 22, 33, 44, 55, 66, 77, 88, 99, 110
First five common multiples of 8 and 11 are 88, 176, 264, 352 and 440.

Question 17.
15 and 25
Answer:
75, 150 and 225.

Explanation:
The multiples of 15 are 15, 30, 45, 60, 75, 90, 105, 120, 135, 150….
The multiples of 25 are 25, 50, 75, 100, 125, 150, 175, 200, 225….
First five common multiples of 15 and 25 are 75, 150 and 225.

Question 18.
7 and 20
Answer:
140, 280, 420, 560 and 700

Explanation:
The multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70…..
The multiples of 20 are 20, 40, 60, 80, 100, 120, 140,160…
First five common multiples of 7 and 20 are 140, 280, 420, 560 and 700.

Find the least common multiple of each pair of numbers.

Question 19.
3 and 10
Answer:
30

Explanation:
By prime factorization,
3 = 3, 10 = 2 x 5
The least common multiple = 3 . 2 . 5 = 30
The least common multiple of 3 and 10 is 30.

Question 20.
7 and 12
Answer:
84

Explanation:
By prime factorization,
7 = 7, 12 = 2 x 2 x 3
The least common multiple = 7 . 2 . 2 . 3
The least common multiple of 7 and 12 is 84.

Question 21.
5 and 8
Answer:
40

Explanation:
By prime factorization,
5 = 5, 8= 2 x 2 x 2
The least common multiple = 5 . 2 . 2 . 2 = 40
The least common multiple of 5 and 8 is 40.

Question 22.
9 and 11
Answer:
99

Explanation:
By prime factorization,
9 = 3 x 3, 11 = 11
The least common multiple = 3 . 3 .11 = 99
The least common multiple of 9 and 11 is 99.

Question 23.
10 and 14
Answer:
70

Explanation:
By prime factorization,
10 = 2 x 5, 14 = 2. 7
The least common multiple = 2 . 5 . 7
The least common multiple of 10 and 14 is 70.

Question 24.
18 and 24
Answer:
72

Explanation:
By prime factorization,
18 = 2 x 3 x 3, 24 = 2 x 2 x 2 x 3
The least common multiple = 2 . 2 . 2 . 3 . 3 = 72
The least common multiple of 18 and 24 is 72.

Find the greatest common factor of each set of numbers.

Question 25.
24, 26, and 84
Answer:
2

Explanation:
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.
The factors of 26 are 1, 2, 13, 26
The factors of 84 are 1, 2, 4, 6, 7, 12, 14, 21, 28, 42, 84
The greatest common factor of 24, 26 and 84 is 2.

Question 26.
30, 48, and 72
Answer:
6

Explanation:
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The greatest common factor of 30, 48 and 72 is 6.

Question 27.
36, 24, and 96
Answer:
12

Explanation:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
The greatest common factor of 36, 24 and 96 is 12.

Question 28.
42, 90, and 81
Answer:
3

Explanation:
The factors of 42 are 1, 2, 3, 6, 7, 14, 21, 42
The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
The factors of 81 are 1, 3, 9, 27, 81
The greatest common factor of 42, 90 and 81 is 3

Question 29.
60, 75, and 102
Answer:
3

Explanation:
The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12,15, 20, 30, 60
The factors of 75 are 1, 3, 5, 15, 25, 75
The factors of 102 are 1, 2, 3, 6, 17, 34, 51, 102
The greatest common factor of 60, 75 and 102 is 3.

Question 30.
63, 105, and 294
Answer:
7

Explanation:
The factors of 63 are 1, 3, 7, 9, 21, 63
The factors of 105 are 1, 3, 5, 7, 15, 21, 35, 105
The factors of 294 are 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, 294
The greatest common factor of 63, 105 and 294 is 7.

Find the least common multiple of each set of numbers.

Question 31.
18, 24, and 42
Answer:

Explanation:
The least common multiple of 18, 24 and 42 is 2 x 3 x 3 x 4 x 7 = 504.

Question 32.
21, 33, and 57
Answer:

Explanation:
The least common multiple of 21, 33 and 57 is 3 x 7 x 11 x 19 = 4389.

Question 33.
14, 30, and 70
Answer:

Explanation:
The least common multiple of 14, 30 and 70 is 2 x 5 x 7 x 3 = 210.

Question 34.
27, 48, and 66
Answer:

Explanation:
The least common multiple of 27, 48 and 66 is 2 x 3 x 9 x 8 x 11 = 4752.

Question 35.
55, 75, and 115
Answer:

Explanation:
The least common multiple of 55, 75 and 115 is 5 x 11 x 15 x 23 = 18975.

Question 36.
78, 90, and 140
Answer:

Explanation:
The least common multiple of 78, 90 and 140 is 2 x 3 x 3 x 5 x 13 x 14 = 16380.

Find the greatest common factor and the least common multiple of each set of numbers.

Question 37.
10, 20, and 25
Answer:
5, 100

Explanation:
By prime factorization,
10 = 2 x 5, 20 = 2 x 2 x 5, 25 = 5 x 5
The least common multiple = 2 . 5 . 2 . 5 = 100
The least common multiple of 10 , 20 and 25 is 100.
The greatest common factor is 5.

Question 38.
16, 28, and 40
Answer:

Greatest common factor is 4.

Explanation:
The least common multiple of 16, 28 and 135 is 560.
By prime factorization:
16 = 2 x 2 x 2 x 2, 28 = 2 x 2 x 7, 40 = 2 x 2 x 2 x 5
common factors are 2 x 2
The greatest common factor is 4.

Question 39.
54, 81, and 135
Answer:
27, 810

Explanation:
By prime factorization,
54 = 2 x 3 x 3 x 3, 81= 3 x 3 x 3 x 3, 135 = 3 x 3 x 3 x 5
The least common multiple =2 . 3 . 3 . 3 . 3  . 5
The least common multiple of 84 , 81 and 135 is 810
The greatest common factor is 3 x 3 x 3 = 27.

Question 40.
72, 144, and 216
Answer:
72, 432

Explanation:
By prime factorization,
72 = 2 x 2 x 2 x 3 x 3, 144 = 2 x 2 x 2 x 2 x 3 x 3, 216 = 2 x 2 x 2 x 3 x 3 x 3
The least common multiple = 2 . 2 . 2 . 2 . 3 . 3 . 3
The least common multiple of 72 , 114 and 216 is 432.
The greatest common factor is 2 x 2 x 2 x 3 x 3 = 72

Solve.

Question 41.
Makayla has two types of ropes. She wants to cut the ropes into pieces of the same length for butterfly knots,

a) Find the greatest possible length that she can cut for each piece, so that no rope will be left unused.
Answer:

b) Write the sum of the two lengths and factor out the number you found in part a). What does the number inside the parentheses represent?
Answer:

Question 42.
Giselle buys two types of flowers, 48 pink roses and 56 white lilies. She combines the flowers to make identical bouquets, with no flowers left over.
a) Find the greatest number of bouquets that Giselle can make.
Answer:
Giselle can make 8 bouquets

Explanation:
By prime factorization,
48 = 2 x 2 x 2 x 2 x 3, 56 = 2 x 2 x 2 x 7
common multiple is 2 x 2 x 2 = 8
Greatest common multiple of 48  and 56 is 8

b) Find the number of pink roses and white lilies in each bouquet.
Answer:
6 pink roses and 7 white lilies

Explanation:
pink roses = 48 = 8 x 6
white lilies = 56 = 8 x 7
So, Each bouquet has 6 pink roses and 7 white lilies.

Question 43.
A red light flashes every 14 minutes. A blue light flashes every 24 minutes. When will the two lights flash together again, if they last flashed together at 8 A.M.?
Answer:

Question 44.
a) Find the product of 84 and 90.
Answer:

Explanation:
The product of 84 and 90 is 7560.

b) Find the product of the greatest common factor and the least common multiple of 84 and 90.
Answer:

Explanation:
Least common multiple of 84 and 90 is 1260,
Greatest common factor of 84 and 90 is 6
Product of the greatest common factor and the least common multiple of 84 and 90 is
1260 x 6 = 7560.

c) What do you observe about your answers to parts a) and b)?
Answer:
The answers of both parts a and b are same.

d) Choose two other numbers and repeat parts a) and b). Do you get the same results?
Answer:
I chose the numbers 6 and 12
Yes, the results are same

Explanation:

The product of the two numbers is equal to the product of the least common multiple and greatest common factor of the numbers.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.2 Prime Factorization to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.2 Answer Key Prime Factorization

Math in Focus Grade 6 Chapter 1 Lesson 1.2 Guided Practice Answer Key

Complete.

Question 1.
Express 48 as a product of its prime factors.
Answer:
Method 1

Method 2

Math in Focus Course 1A Practice 1.2 Answer Key

Question 1.
Copy the array of numbers. Circle all the prime numbers.

Answer:

Explanation:
I circled all the prime numbers between 1 and 30.

Express each number as a product of its prime factors.

Question 2.
6
Answer:

6 = 2 x 3

Explanation:
2 and 3 are the prime factors of 6.

Question 3.
15
Answer:

15 = 3 x 5

Explanation:
3 and 5 are the prime factors of 15.

Question 4.
36
Answer:

36 = 2 x 2 x 3 x 3

Explanation:
2 and 3 are the prime factors of 36.

Question 5.
78
Answer:

78 = 2 x 3 x 13

Explanation:
2, 3 and 13 are the prime factors of 78.

Question 6.
184
Answer:

184 = 2 x 2 x 2 x 23

Explanation:
2 and 23 are the prime factors of 184.

Question 7.
360
Answer:

360 = 2 x 2 x 2 x 3 x 3 x 5

Explanation:
2, 3 and 5 are the prime factors of 360.

Question 8.
24
Answer:

24 = 2 x 2 x 2 x 3

Explanation:
2 and 3 are the prime factors of 24.

Question 9.
49
Answer:

49 = 7 x 7

Explanation:
7 is the only prime factor of 49.

Question 10.
81
Answer:

81 = 3 x 3 x 3 x 3

Explanation:
3 is the prime factor of 81.

Question 11.
144
Answer:

144 = 2 x 2 x 2 x 2 x 3 x 3

Explanation:
2 and 3 are the prime factors of 144.

Question 12.
245
Answer:

245 = 5 x 7 x 7

Explanation:
5 and 7 are the prime factors of 245.

Question 13.
510
Answer:

510 = 2 x 3 x 5 x 17

Explanation:
2, 3, 5 and 17 are the prime factors of 510.

Question 14.
250
Answer:

250 = 2 x 5 x 5 x 5

Explanation:
2 and 5 are the prime factors of 250.

Question 15.
1,089
Answer:

1089 = 3 x 3 x 11 x 11

Explanation:
3 and 11 are the prime factors of 1089.

Question 16.
4,725
Answer:

4725 = 3 x 3 x 3 x 5 x 5 x 7.

Explanation:
3, 5 and 7 are the prime factors of 4725.

Question 17.
900
Answer:

900 = 2x 2 x 3 x 3 x 5 x 5

Explanation:
2, 3 and 5 are the prime factors of 900.

Question 18.
27,000
Answer:

27000 = 2x 2 x 2 x 3 x 3 x 3 x 5 x 5 x 5.

Explanation:
2, 3 and 5 are the prime factors of 27000.

Solve.

Question 19.
Math Journal Describe the steps for finding the prime factors of 42.
Answer:

Question 20.
400 written as a product of its prime factors is 2 × 2 × 2 × 2 × 5 × 5. Write 800 as a product of its prime factors.
Answer:
2 x 2 × 2 × 2 × 2 × 5 × 5 = 800

Explanation:
800 written as a product of its prime factors is 2 x 2 × 2 × 2 × 2 × 5 × 5.

Question 21.
Given that 320 written as a product of its prime factors is 2 × 2 × 2 × 2 × 2 × 2 × 5, write 3,200 as a product of its prime factors.
Answer:
2 x 2 × 2 × 2 × 2 × 2 × 2 × 5 x 5 = 3200

Explanation:
3200 written as a product of its prime factors is 2 x 2 × 2 × 2 × 2 × 2 × 2 × 5 x 5 .

Question 22.
2,700 written as a product of its prime factors is 2 × 2 × 3 × 3 × 3 × 5 × 5. Write 270 as a product of its prime factors.
Answer:
2 × 3 × 3 × 3 × 5 = 270

Explanation:
270 written as a product of its prime factors is 2 ×  3 × 3 × 3 × 5.

Question 23.
It is given that 4,800 can be expressed in terms of its prime factors as 2 × 2 × 2 × 2 × 2 × 2 × 3 × 5 × 5.

a) Write 1,200 as a product of its prime factors.
Answer:
2 x 2 x 2 x 2 x 3 x 5 x 5 = 1200

Explanation:
1200 can be expressed in terms of its prime factors as 2 x 2 x 2 x 2 x 3 x 5 x 5.

b) Now, write 120 as a product of its prime factors.
Answer:
2 x 2 x 2 x 3 x 5 = 120

Explanation:
120 can be expressed in terms of its prime factors as 2 x 2 x 2 x 3 x 5 .

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 5 Lesson 5.2 Real-World Problems: Rates and Unit Rates to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 5 Lesson 5.2 Answer Key Real-World Problems: Rates and Unit Rates

Math in Focus Grade 6 Chapter 5 Lesson 5.2 Guided Practice Answer Key

Solve.

Question 1.
A unicycle wheel makes 196 revolutions in 7 minutes.
a) At this rate, how many revolutions does it make in 1 minute?
The unicycle wheel makes the same number of revolutions every minute.

Answer:
28 revolutions
Explanation:

b) At this rate, how many revolutions does the unicycle wheel make in 15 minutes?

min → × = revolutions
The unicycle makes revolutions in 15 minutes.
Answer:
420 revolutions
Explanation:

15 min → 28 × 15 = 420 revolutions
The unicycle makes 420 revolutions in 15 minutes.

Question 2.
Megan babysits for 5 hours and earns $60.
a) At this rate, how much does she earn in 1 hour?
hours → $
1 hour → $ ÷ = $
She earns $ in 1 hour.
Answer:
$ 12 in 1 hour.
Explanation:
5 hours → $ 60
1 hour → $ 60 ÷ 5 = $12
She earns $ 12 in 1 hour.

b) At this rate, how much will Megan earn if she babysits for 14 hours?
14 hours → × = $
Megan will earn $ if she babysits for 14 hours.
Answer:
$168 for 14 hours
Explanation:
14 hours → 14 × 12 = $168
Megan will earn $ 168 if she babysits for 14 hours.

Question 3.
The table shows the charges for renting a bicycle.
Tom rented a bicycle from 10 A.M. to 2 P.M. ON the same day. How much did he pay for renting the bicycle?

Total number of hours = h
Charge for first hour = $
Charge for each additional 1 hour = 2 × Cost for each additional \(\frac{1}{2}\) hour
= 2 × $
= $
Charge for last three hours = × $
= $
Total charge = $ + $
= $
Tom paid $ for renting the bicycle.
Answer:
$18
Explanation:
Total number of hours = 4 h
Charge for first hour = $3.00
Charge for each additional 1 hour = 2 × Cost for each additional \(\frac{1}{2}\) hour
= 2 × $2.5
= $5.0
Charge for last three hours = 3 × $5
= $15.00
Total charge = $3.00 + $15.00
= $18.00
Tom paid $18.00 for renting the bicycle.

Question 4.
Chloe scored 87 points in 5 basketball games, and Fiona scored 45 points in 2 basketball games. Which of the two players scored more points per game? Explain.
Chloe: .
5 games → points
1 game → ÷ 5 = points
Chloe scored points per game.

Fiona: .
2 games → points
1 game → ÷ = points
Fiona scored points per game.

Comparing the number of points each player scored per game, scored a higher number of points per game.
So, scored more points per game.
Answer:
5.1 scored more points per game
Explanation:
Chloe: .
5 games → 87 points
1 game → 87 ÷ 5 = 17.4 points
Chloe scored 17.4 points per game.

Fiona: .
2 games → 45 points
1 game → 45 ÷ 2 = 22.5 points
Fiona scored 22.5 points per game.

Comparing the number of points each player scored per game, Fiona scored a higher number of points per game.
22.5 – 17.4 = 5.1
So, 5.1 scored more points per game.

Question 5.
A high-speed train can travel at a speed of 65 meters per second. How far can the train travel in 2 seconds?

Answer:
130 M
Explanation:

Question 6.
The distance between City X and City Y is 216 kilometers. Mr. Thomas rides his motorcycle at a speed of 54 kilometers per hour. How long does he take to travel from City X to City Y?
Method 1
km → h
km → \(\frac{?}{?}\) = h
Mr. Thomas takes hours to travel from City X to City Y.

Method 2
Time = Distance ÷ Speed
= ÷
= h
Mr. Thomas takes hours to travel from City X to City Y.
Answer:
4 hours
Explanation:
Method 1
216 km → h
216 km → \(\frac{216}{54?}\) = 4 h
Mr. Thomas takes 4 hours to travel from City X to City Y.

Method 2
Time = Distance ÷ Speed
= 216 ÷ 54
= 4 h
Mr. Thomas takes 4 hours to travel from City X to City Y.

Question 7.
The distance between Town P and Town Q is 80 miles, and the distance between Town Q and Town R is 320 miles. A van takes 2\(\frac{1}{2}\) hours to travel from Town P to Town Q. It takes another 5 hours to travel from Town Q to Town R. Find the average speed of the van for the whole journey.

Total distance from Town P to Town R = 80 +
= mi
Total time taken to travel from Town P to Town R = 2\(\frac{1}{2}\) +
= h

= \(\frac{?}{?}\)
= ÷
= mi/h or mph
The average speed of the van is miles per hour.
Answer:
53.33 min/hr or 53 mph
Explanation:

Total distance from Town P to Town R = 80 + 320 = 400 mi
Total time taken to travel from Town P to Town R = 2\(\frac{1}{2}\) + 5
= \(\frac{15}{2}\) h
=7\(\frac{1}{2}\) h

= \(\frac{?}{?}\)
= 400 ÷7 \(\frac{1}{2}\)
= 53.33 min/hr or 53 mph
The average speed of the van is 53.33 miles per hour.

Question 8.
Celia ran around a 400-meter track two times. It took her 4 minutes to run around the track once, and 6 minutes to run around it again. Find Celia’s average speed.
Total distance Celia ran = 2 ×
= m
Total time taken to run around the track twice = +
= min

= \(\frac{?}{?}\)
= m/min
Celia’s average speed was meters per minute.
Answer:
80 meters per minute.
Explanation:
Total distance Celia ran = 2 × 400 = 800 m
Total time taken to run around the track twice = 4 + 6 = 10 min

= \(\frac{800}{10}\)
= 80 m/min
Celia’s average speed was 80 meters per minute.

Math in Focus Course 1A Practice 5.2 Answer Key

Solve. Show your work.

Question 1.
A tennis ball machine can launch 60 tennis balls in 12 minutes. At this rate, how many tennis balls can it launch in 2 hours?
Answer:
600 Tennis balls
Explanation:
There are 120 minutes in 2 hours
10 sets of 12 minutes in 120 minutes.
\(\frac{120}{12}\) x 60 = 600
Therefore, 10 sets of 60 balls launched.

Question 2.
Water flows from a faucet at a rate of 5 liters every 25 seconds.
a) At this rate, how much water will flow from the faucet in 45 seconds?
Answer:
9 liters
Explanation:
The rate per 5 seconds, given in the first question is 45 seconds.
\(\frac{5}{25}\) = \(\frac{11}{5}\)
The x amount of liters in 45 seconds.
\(\frac{x}{45}\) = \(\frac{11}{5}\)
5x = 45
x = 9 liters

b) At this rate, how long will it take to collect 60 liters of water?
Answer:
300 seconds or 5 hours
Explanation:
9 liters for every 45 seconds.
60 liters in x amount of seconds.
\(\frac{60}{x}\) = \(\frac{11}{5}\)
x = 60 x 5
x = 300 sec

Question 3.
There are 1,600 kilocalories in the 5 cups of dog food that Mike gives his adult dog. Mike gives his puppy 2 cups of the same dog food. How many kilocalories are there in this 2-cup serving?
Answer:
640 kilocalories
Explanation:
There are 1,600 kilocalories in the 5 cups of dog food that Mike gives his adult dog.
Kilocalories = \(\frac{1,600}{5}\)
Mike gives his puppy 2 cups of the same dog food.
Total kilocalories are there in this 2-cup serving
Kilocalories = 320 per cup
Kilocalories for 2 cups = 320 x 2 = 640 for 2 cups

Question 4.
The table shows the postal charges for sending letters to Country Y. How much does it cost to send a letter weighing 60 grams to Country Y?

Answer:
$1.70
Explanation:
Cost of a letter weighing 60 grams to Country
first 20 g = 50 cents
next 40 g = 30 cents x 4 = 120 cents
weighing 60 grams to Country Y total  = 120 + 50
= 170 cents or $1.70

Question 5.
A vehicle traveled at a speed of 54 kilometers per hour for 3 hours. Find the distance traveled.
Answer:
162 kilometers
Explanation:
A vehicle traveled at a speed of 54 kilometers per hour
The distance traveled for 3 hours
1 hour = 54 kilometers
3 hours = 54 x 3 = 162 kmph.

Question 6.
A pigeon can fly at a speed of 84 kilometers per hour. How long does it take the pigeon to fly 7 kilometers?
Answer:
\(\frac{1}{12}\)minutes
Explanation:
A pigeon can fly at a speed of 84 kilometers per hour.
\(\frac{84}{1}\) = \(\frac{7}{x}\)
84x = 7
x = \(\frac{7}{84}\)
The distance taken by pigeon to fly 7 kilometers
= \(\frac{1}{12}\)

Question 7.
Karen walks home from school at a speed of 5 kilometers per hour. She takes 12 minutes to reach home. What is the distance between her school and her home? (Hint: Convert the time from minutes to hours.)
Answer:
1 kilometer
Explanation:
Distance = speed x time
= 5 x 12
=5 x 12/60 km
=60/60
=1 km

Question 8.
Kayla ran from her home to a beach at a speed of 6 meters per second. The distance from her home and the beach was 756 meters.
a) How long did she take to run from her home to the beach?
Answer:
126 seconds
Explanation:
Time = Distance ÷ Speed
Kayla ran from her home to a beach at a speed of 6 meters per second.
The distance from her home and the beach was 756 meters.
Distance = 756m
Speed= 6 meters per second
756m ÷ 6m/s = 126s

b) If Kayla wants to take 18 fewer seconds to reach the beach, at what speed must she run?

Answer:
7 meter per second
Explanation:
speed = Distance /time
= 756 / 108    (126 – 18 = 108sec)
= 7 m/s

Question 9.
Car A travels 702 miles on 12 gallons of gasoline. Car B travels 873 miles on 15 gallons of gasoline. David wants to buy a car with the lowest fuel consumption. Find out the distance traveled by each car per gallon of gasoline. Then tell which of the two cars, A, or B, David should buy.
Answer:
Car A
Explanation:
Car A travels 702 miles on 12 gallons of gasoline
= \(\frac{702}{12}\)
= 58.5 miles per gallon

Car B travels 873 miles on 15 gallons of gasoline
= \(\frac{873}{15}\)
= 58.2 miles of gallon
Car A,  David should buy.

Question 10.
Post A and Post B are 120 meters apart. Post B and Post C are 300 meters apart. Ben cycled from Post A to Post B in 15 seconds. Then he cycled from Post B to Post C in 55 seconds. Find Ben’s average speed for the distance from Post A to Post C.
Answer:
6 meters per second
Explanation:
Post A to B
= \(\frac{120}{15}\)
= 8m/s
Post B to C
= \(\frac{300}{55}\)
= 5.45 m/s
average speed for the distance from Post A to Post C.
\(\frac{8 + 5.45}{2}\)
= 6.72m/s

Question 11.
Mr. Alan drove for 2\(\frac{1}{5}\) hours at a speed of 70 kilometers per hour. He then drove another 224 kilometers. He took 5 hours for the whole journey. What was Mr. Alan’s average speed for the whole journey?
Answer:
57.4 KMPH
Explanation:
Mr. Alan drove for 2\(\frac{1}{5}\) hours at a speed of 70 kilometers per hour
Distance = speed x time
Speed = Distance /Time
= \(\frac{224}{5}\)
= 44.5 KMPH
Mr. Alan’s average speed for the whole journey
= (70 + 44.5)/2
= 57.4 KMPH

Question 12.
A family took 2 hours to drive from City A to City B at a speed of 55 miles per hour. On the return trip, due to a snowstorm, the family took 3 hours to travel back to City A.
a) How many miles did the family travel in all?
Answer:
220 miles
Explanation:
City A to B
Distance = Speed x time
= 55 x 2 = 110 km
Return journey from city B to A distance 110 km
Distance = Speed x time
110 = Speed x 3
Speed = 36.66 miles per hour

b) What was the average speed for the entire trip?
Answer:
44 miles per hour
Explanation:
Return journey from city B to A distance 110 km
Distance = Speed x time
110 = Speed x 3
Speed = 36.66 miles per hour
the average speed for the entire trip
(55 + 36.66)/2 = 45.83 miles per hour

Brain @ Work

Question 1.
The distance between Point A and Point B is 3,120 meters. Caroline leaves Point A and Laura leaves Point B at the same time. The two girls cycle toward each other until they meet at Point C. Caroline’s speed is 7.2 meters per second, and Laura’s speed is 8.4 meters per second.
a) How long does Laura take to reach Point C?
Answer:
1,680 minutes
Explanation:
7.2 + 8.4 = 15.6 m/s
Time = Distance / Speed
= 3120/15.6
= 200 s
Laura take to reach Point C
Distance = Time x speed
= 200 x 8.4 = 1680 min

b) What is the distance between Point A and Point C?

Answer:
Caroline leaves Point A
Explanation:
Distance from Point A to C
A = 3,120 and C = 1,680
3,120 – 1,680 = 1,440m