Hillary

This handy Math in Focus Grade 4 Workbook Answer Key Chapter 13 Symmetry detailed solutions for the textbook questions.

Math in Focus Grade 4 Chapter 13 Answer Key Symmetry

Math Journal

Complete.

Question 1.

Explain why the dotted line is the line of symmetry for the figure.
Answer:
If a figure can be folded or divided into half so that the two halves match exactly then such a figure is called a symmetric figure. The figure above is symmetric.
The dotted line in above symmetric figure that divides the figure into two equal halves is called the line of symmetry.

Question 2.

Does the square have rotational symmetry about the center shown? Explain.
Answer:
Yes, The square have rotational symmetry for the center shown in the above figure.
Explanation:
If a figure is rotated around a center point and it still appears exactly as it did before the rotation, it is said to have rotational symmetry. A number of shapes like squares, circles, regular hexagons etc. have rotational symmetry.

Put On Your Thinking Cap!

Challenging Practice

Shade the correct squares so that the pattern of shaded squares has line symmetry about the given dotted line.

Question 1.

Answer:

Shaded the correct squares in the above figure. The pattern of shaded squares has line symmetry for the given dotted line.

Question 2.

Answer:

Shaded the correct squares in the above figure. The pattern of shaded squares has line symmetry for the given dotted line.

In the square grid below, design a symmetric pattern that has both line symmetry about the given dotted line and rotational symmetry.

Question 3.

Answer:

In the above square grid, designed a symmetric pattern that has both line symmetry for the given dotted line and rotational symmetry.

Put On Your Thinking Cap!

Problem Solving

Add one unit square to each figure to make it symmetric about the given dotted line.

Question 1.

Answer:

Added one unit square to the above figure to make it symmetric for the given dotted line.

Question 2.

Answer:

Added one unit square to the above figure to make it symmetric for the given dotted line.

Shade unit squares in each pattern so that it has line symmetry and rotational symmetry.

Question 3.

Answer:

Shaded unit squares in above pattern. Now the above figure has both line symmetry and rotational symmetry.

Question 4.

Answer:

Shaded unit squares in above pattern. Now the above figure has both line symmetry and rotational symmetry.

Solve.

Question 5.
Using the digits 0, 1, 6, 8, and 9, write down all the possible three-digit numbers that have rotational symmetry. The digits can be used more than once.
Answer:
Three digit numbers:
(000, 010, 080 are not considered generally as a three-digit number)
101, 609, 808, 906,
replace the middle digit successively by 1 and 8 gives
111, 619, 818, 916,
181, 689, 888, 986
for a total of 12 numbers

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Chapter 12 Practice 1 Real-World Problems: One-Step Problems to score better marks in the exam.

Math in Focus Grade 3 Chapter 12 Practice 1 Answer Key Real-World Problems: One-Step Problems

Solve. Use bar models to help you.

Question 1.
A restaurant has two tables of different lengths. One is 146 centimeters long. The other is 185 centimeters long. What is their total length? Write your answer in meters and centimeters.

Answer:
There total length is 331 centimeters
There total length is 3.31 meters
Explanation:
A restaurant has two tables of different lengths. One is 146 centimeters long.
The other is 185 centimeters long.
145 + 185 = 331 cm
3.31 meters
1 meter = 100 centimeters

Question 2.
Jim is preparing for a race. He runs around the track 3 times each day. If he runs 300 meters a day, what is the length of the track?
Answer:
100 meters
Explanation:
Jim is preparing for a race. He runs around the track 3 times each day.
If he runs 300 meters a day,
300 ÷ 3 = 100 meters is the length of the track

Question 3.
A baby elephant has a mass of 1 45 kilograms. The mass of its sister is 5 times as much. What is the mass of its sister?
Answer:
The mass of its sister = 725 kilograms
Explanation:
A baby elephant has a mass of 1 45 kilograms. The mass of its sister is 5 times as much.
145 x 5 = 725

Question 4.
James has a fish tank with a capacity of 24 liters. He uses a 2-liter pail to fill the tank. How many pails of water does he use?

Answer:
12 pails of water that he use
Explanation:
James has a fish tank with a capacity of 24 liters.
He uses a 2-liter pail to fill the tank.
24 ÷  2 = 12

Question 5.
A watering can contains 980 milliliters of water. Some water is used to water the plants. In the end, 350 milliliters of water are left. How much water is used to water the plants?

Answer:
630 milliliters water is used to water the plants
Explanation:
A watering can contains 980 milliliters of water.
Some water is used to water the plants.
In the end, 350 milliliters of water are left.
980 – 350 = 630

Question 6.
A baker has 2,000 grams of flour. He uses 425 grams of it. What is the mass of the flour left? Give your answer in kilograms and grams.
Answer:
In kilograms = 1.575
In grams = 1575
Explanation:
A baker has 2,000 grams of flour. He uses 425 grams of it.
2000 – 425 = 1575
1 kg = 1000 grams
1.575 grams

Question 7.
Max buys 875 grams of nuts on Monday. He buys 955 grams of nuts on Tuesday. What is the total mass of nuts he buys? Give your answer in kilograms and grams.
Answer:
the total mass of nuts he buys = 1830 grams
In kilograms = 1.830 Kilograms.
Explanation:
Max buys 875 grams of nuts on Monday. He buys 955 grams of nuts on Tuesday.
875 + 955 = 1830 grams

Question 8.
Mrs. Spence has 4 bottles of orange juice. Each bottle contains 125 milliliters of juice. She pours all the juice into an empty container. How much orange juice is in the container?
Answer:
1 liter orange juice is in the container
Explanation:
Mrs. Spence has 4 bottles of orange juice
Each bottle contains 125 milliliters of juice.
She pours all the juice into an empty container.
125 x 4 = 1000 = 1 liter

Go through the Math in Focus Grade 3 Workbook Answer Key Chapter 2 Practice 1 Mental Addition to finish your assignments.

Math in Focus Grade 3 Chapter 2 Practice 1 Answer Key Mental Subtraction

Add mentally. First, add the tens. Then, add the ones.

Example

Question 1.
24 + 55 = ?
24 + 50 = ___
___ + ___ = ___
So, 24 + 55 = ____

Answer:

24 + 50 = 74
74 + 5 = 79
So, 24 + 55 = 79

Question 2.
22 + 64 = ?
20 + 64 = ___
___ + ___ = ____
So, 22 + 64 = ___

Answer:

20 + 64 = 84
84 + 2 = 86
So, 22 + 64 = 86

Add mentally. Use number bonds to help you.

Example

Question 3.
37 + 45 = ?
37 + 50 = __
___ – ___ = ___
So, 37 + 45  = ___

Answer:

37 + 50 = 87
87 – 5 = 82
So, 37 + 45  = 82

Question 4.
46 + 34 = ?
46 + 40 = ___
__ – __ = ___
So 46 + 34 = ___

Answer:

46 + 40 = 86
86 – 6 = 80
So 46 + 34 = 80

Add mentally. Use number bonds to help you.

Question 5.
41 + 43 = ___
Answer:
41 + 43
40 + 40 = 80
80 + 1 + 3 = 84
So, 41 + 43 = 84

Question 6.
31 + 64 = ___
Answer:
31 + 64
30 + 60 = 90
90 + 1 + 5 = 95
So, 31 + 64 = 95

Question 7.
15 + 47 = ___
Answer:
15 + 47
15 + 50 = 65
65 – 3 = 62
So, 15 + 47 = 62

Question 8.
46 + 48 = ___
Answer:
46 + 48
50 + 50 = 100
100 – 4 -2 = 94
So, 46 + 48 = 94

Go through the Math in Focus Grade 3 Workbook Answer Key Chapter 3 Practice 1 Addition Without Regrouping to finish your assignments.

Math in Focus Grade 3 Chapter 3 Practice 1 Answer Key Addition Without Regrouping

Add.

Example

Question 1.

Answer:

Explanation:
6,210 + 765 = 6,975.

Question 2.

Answer:

Explanation:
5,324 + 3,351 = 8,675.

Question 3.

Answer:

Explanation:
5,413 + 1,382 = 6,795.

Question 4.

Answer:

Explanation:
7,363 + 1,406 = 8,769.

Question 5.

Answer:

Explanation:
1,048 + 3,430 = 4,478.

Question 6.

Answer:

Explanation:
3,157 + 2,242 = 5,399.

Add.

Example

Question 7.
5,362 + 506 = ____

Answer:
5,362 + 506 = 5,868.

Explanation:

Question 8.
6,542 + 3,050 = ____

Answer:
6,542 + 3,050 = 9,592.

Explanation:

Question 9.
4,632 + 5,306 = ____

Answer:
4,632 + 5,306 = 9,938.

Explanation:

Question 10.
741 + 2,100 = ____

Answer:
741 + 2,100 = 2,841.

Explanation:

Find the sum. Use base-ten blocks to help you.
Example
The sum of 6,324 and 251 is 6,575

Question 11.
The sum of 8,624 and 1,362 is ____
Answer:
The sum of 8,624 and 1,362 is 9,986.

Explanation:

Question 12.
The sum of 3,452 and 5,037 is ____
Answer:
The sum of 3,452 and 5,037 is 8,489.

Explanation:

Add
Example

Question 13.
3,005 + 4 = ___
Answer:
3,005 + 4 = 3,009.

Explanation:
3,005 + 4 = 3,009.

Question 14.
6,015 + 24 = ___
Answer:
6,015 + 24 = 6,039.

Explanation:
6,015 + 24 = 6,039.

Question 15.
2,021 + 42 = ___
Answer:
2,021 + 42 = 2,063.

Explanation:
2,021 + 42 = 2,063.

Question 16.
8,600 + 300 = ___
Answer:
8,600 + 300 = 8,900.

Explanation:
8,600 + 300 = 8,900.

Question 17.
2,362 + 606 = ___
Answer:
2,362 + 606 = 2,968.

Explanation:
2,362 + 606 = 2,968.

Question 18.
3,633 + 1,143 = ___
Answer:
3,633 + 1,143 = 4,776.

Explanation:
3,633 + 1,143 = 4,776.

Question 19.
4,361 + 3,015 = ___
Answer:
4,361 + 3,015 = 7,376.

Explanation:
4,361 + 3,015 = 7,376.

Write the matching letters of each answer to find out what “Buenas tardes” means.
Question 20.

Answer:
good afternoon.

Explanation:

3,005 + 4 = 3,009.
6,015 + 24 = 6,039.
2,021 + 42 = 2,063.
8,600 + 300 = 8,900.
2,362 + 606 = 2,968.
3,633 + 1,143 = 4,776.
4,361 + 3,015 = 7,376.

Add. Show your work.
Example

Question 21.
4,094 + 803 = ____

Answer:
4,094 + 803 = 4,897.

Explanation:

Question 22.
5,051 + 2,136 = ____

Answer:
5,051 + 2,136 = 7,187.

Explanation:

Question 23.
7,423 + 1,362 = ____

Answer:
7,423 + 1,362 = 8,785.

Explanation:

Question 24.
6,036 + 3,112 = ___

Answer:
6,036 + 3,112 = 9,148.

Explanation:

Question 25.
8,999 + 1,000 = ____

Answer:
8,999 + 1,000 = 9,999.

Explanation:

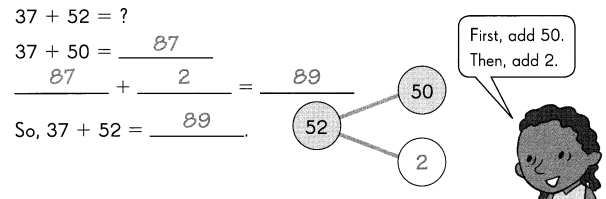
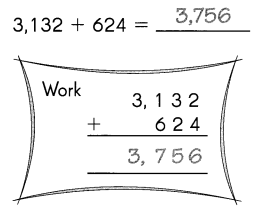
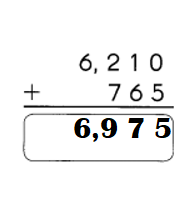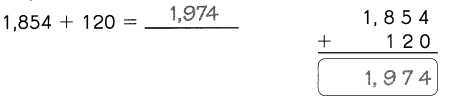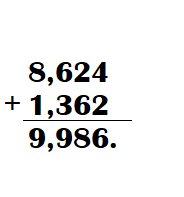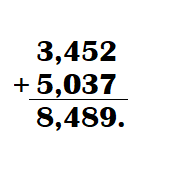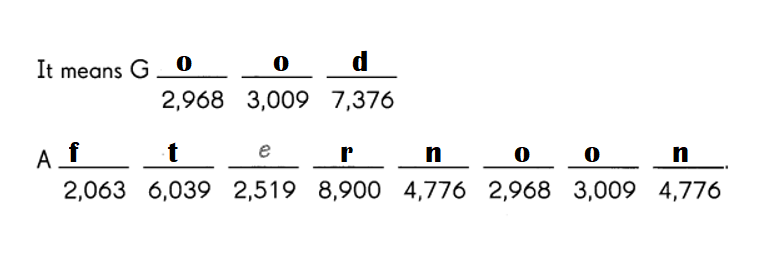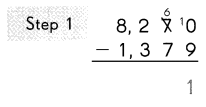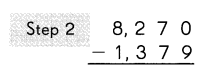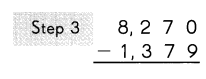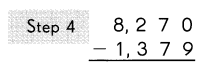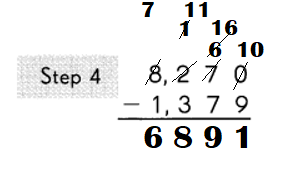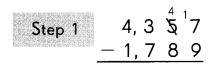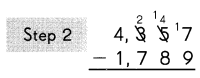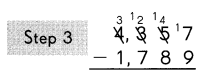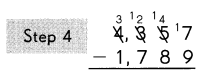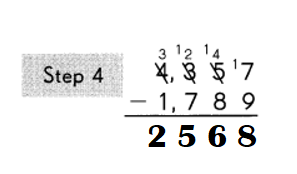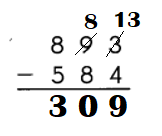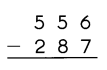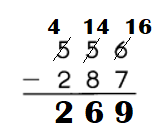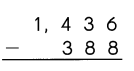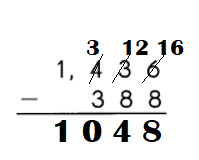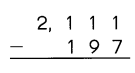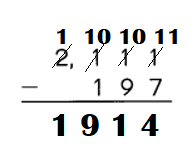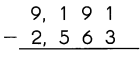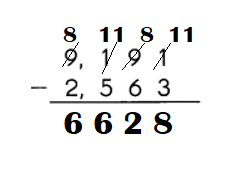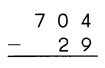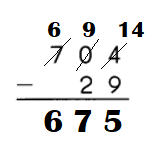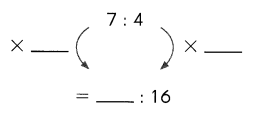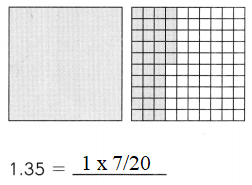Go through the Math in Focus Grade 3 Workbook Answer Key Chapter 4 Practice 3 Subtraction with Regrouping in Ones, Tens, Hundreds, and Thousands to finish your assignments.

Math in Focus Grade 3 Chapter 4 Practice 3 Answer Key Subtraction with Regrouping in Ones, Tens, Hundreds, and Thousands

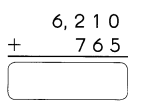
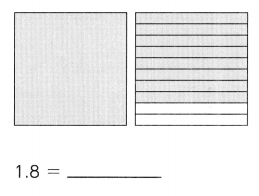
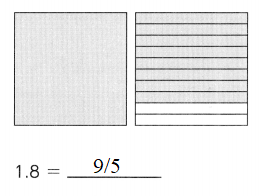
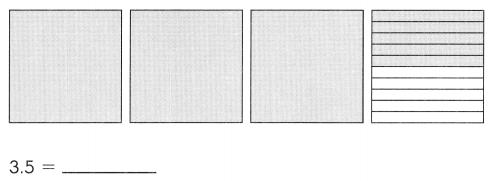
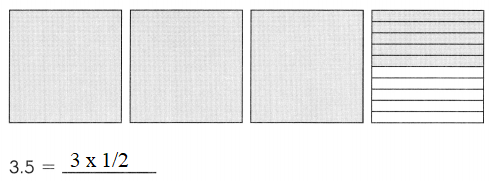
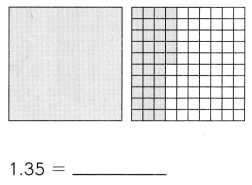
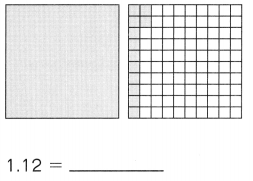
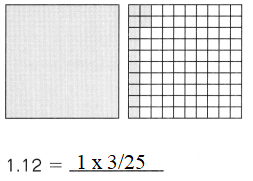
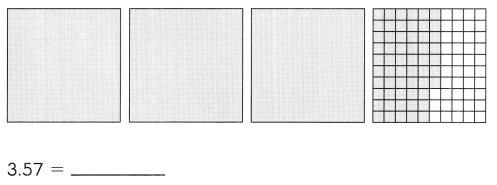
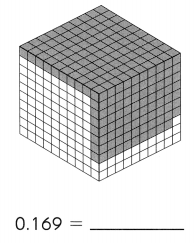
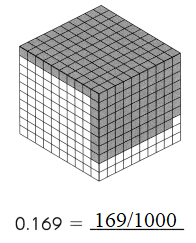
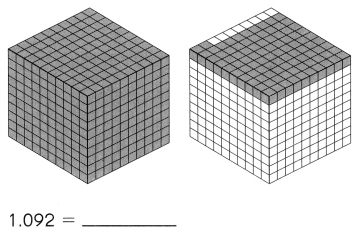
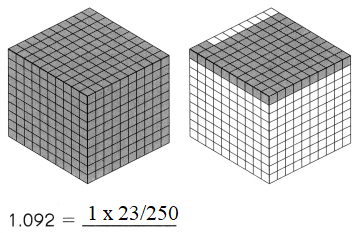
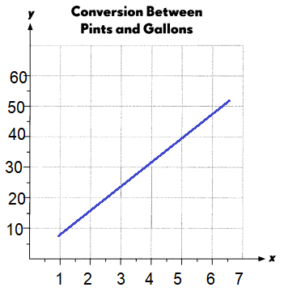
Subtract. Fill in the blanks.

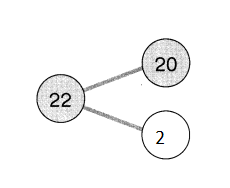
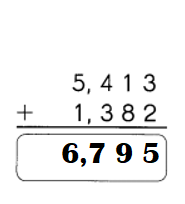
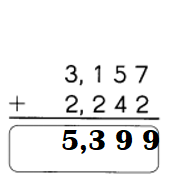
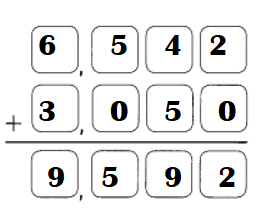
Question 1.
Example

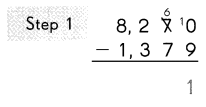
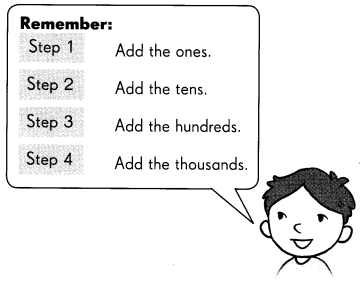
Subtract the ones.
9 ones cannot be subtracted from 0 ones.
So, regroup the tens and ones.
7 tens 0 ones
= __ tens ___ ones

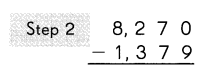
Subtract the tens.
7 tens cannot be subtracted from 6 tens.
So, regroup the hundreds and tens.
2 hundreds 6 tens
= __ hundred ___ tens
Subtract the hundreds.

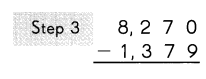
3 hundreds cannot be subtracted from
___ hundred.
So, regroup the thousands and hundreds.
8 thousands 1 hundred
= ___ thousands ___ hundreds

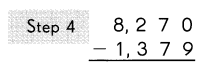
Subtract the thousands.

Answer:
8270 – 1379 = 6891.

Explanation:

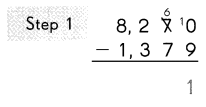
Subtract the ones.
9 ones cannot be subtracted from 0 ones.
So, regroup the tens and ones.
7 tens 0 ones
= 6 tens 10 ones.

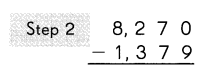
Subtract the tens.
7 tens cannot be subtracted from 6 tens.
So, regroup the hundreds and tens.
2 hundreds 6 tens
= 1 hundred 16 tens.
Subtract the hundreds.

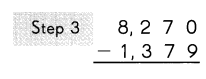
3 hundreds cannot be subtracted from 2 hundred.
So, regroup the thousands and hundreds.
8 thousands 1 hundred
= 7 thousands 11 hundreds

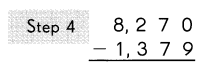
Subtract the thousands.

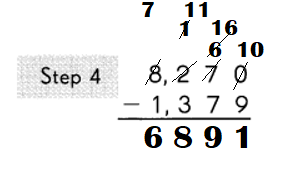
Subtract. Fill in the blanks.

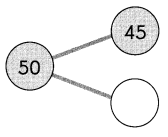
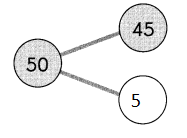
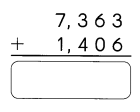
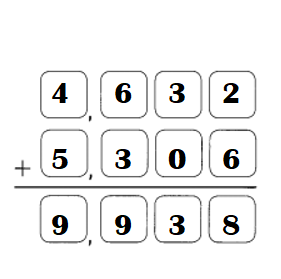
Question 2.

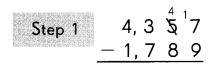
Subtract the ones.
9 ones cannot be subtracted from 7 ones.
So, regroup the tens and ones.
5 tens 7 ones
= ___________ tens ___________ ones

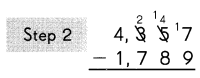
Subtract the tens.
8 tens cannot be subtracted from ___________ tens.
So, regroup the hundreds and tens.
3 hundreds 4 tens
= __________ hundreds __________ tens

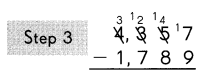
Subtract the hundreds.
7 hundreds cannot be subtracted from
___________ hundreds.
So, regroup the thousands and hundreds.
4 thousands 2 hundreds.
= ____ thousands __ hundreds

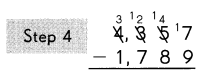
Subtract the thousands.

Answer:
4357 – 1789 = 2568.

Explanation:

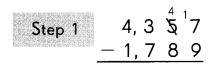
Subtract the ones.
9 ones cannot be subtracted from 7 ones.
So, regroup the tens and ones.
5 tens 7 ones
= 4 tens 17 ones.

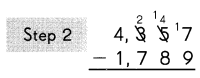
Subtract the tens.
8 tens cannot be subtracted from 4 tens.
So, regroup the hundreds and tens.
3 hundreds 4 tens
= 2 hundreds 14 tens.

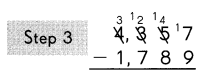
Subtract the hundreds.
7 hundreds cannot be subtracted from
2 hundreds.
So, regroup the thousands and hundreds.
4 thousands 2 hundreds.
= 3 thousands 12 hundreds.

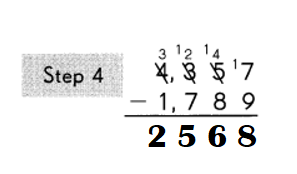
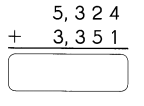
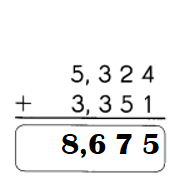
Subtract. Regroup when needed.

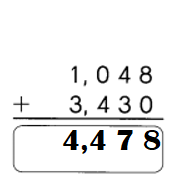
Question 3.

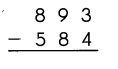
Answer:

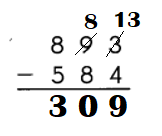
Explanation:
Step:1
Subtract the ones.
3 ones cannot be subtracted from 4 ones.
So, regroup the tens and ones.
9 tens 3 ones
= 8 tens 13 ones.

Step:2:
Subtract the tens.

Step:3
Subtract the hundreds.

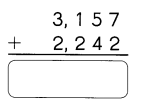
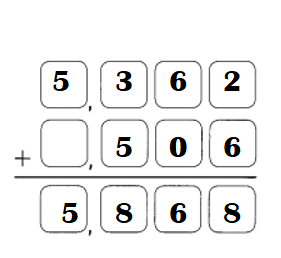
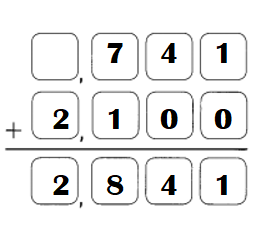
Question 4.

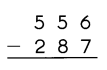
Answer:

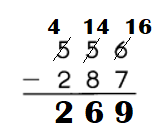
Explanation:
Step:1
Subtract the ones.
7 ones cannot be subtracted from 6 ones.
So, regroup the tens and ones.
5 tens 6 ones
= 4 tens 16 ones.

Step:2:
Subtract the tens.
4 tens cannot be subtracted from 8 tens.
So, regroup the hundreds and tens.
5 hundreds 4 tens
= 4 hundreds 14 tens.

Step:3
Subtract the hundreds.

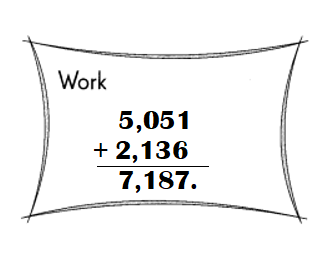
Question 5.

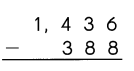
Answer:

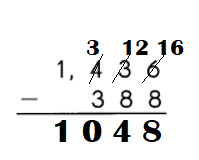
Explanation:
Step:1
Subtract the ones.
8 ones cannot be subtracted from 6 ones.
So, regroup the tens and ones.
3 tens 6 ones
= 2 tens 16 ones.

Step:2:
Subtract the tens.
8 tens cannot be subtracted from 2 tens.
So, regroup the hundreds and tens.
4 hundreds 2 tens
= 3 hundreds 12 tens.

Step:3
Subtract the hundreds.

Question 6.

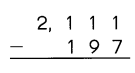
Answer:

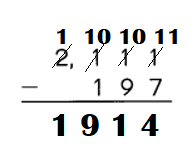
Explanation:
Step:1
Subtract the ones.
7 ones cannot be subtracted from 1 ones.
So, regroup the tens and ones.
1 tens 1 ones
= 10 tens 11 ones.

Step:2:
Subtract the tens.
9 tens cannot be subtracted from 0 tens.
So, regroup the hundreds and tens.
1 hundreds 0 tens
= 0 hundreds 10 tens.

Step:3
Subtract the hundreds.
1 hundreds cannot be subtracted from
0 hundreds.
So, regroup the thousands and hundreds.
2 thousands 0 hundreds.
= 1 thousands 10 hundreds.

Step:4
Subtract the thousands.

Question 7.

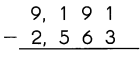
Answer:

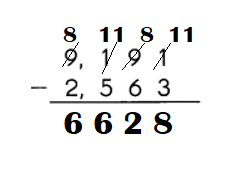
Explanation:
Step:1
Subtract the ones.
3 ones cannot be subtracted from 1 ones.
So, regroup the tens and ones.
9 tens 1 ones
= 8 tens 11 ones.

Step:2:
Subtract the tens.

Step:3
Subtract the hundreds.
5 hundreds cannot be subtracted from 1 hundreds.
So, regroup the thousands and hundreds.
9 thousands 1 hundreds.
= 8 thousands 11 hundreds.

Step:4
Subtract the thousands.

Question 8.

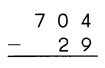
Answer:

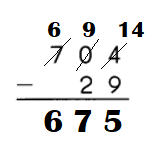
Explanation:
Step:1
Subtract the ones.
9 ones cannot be subtracted from 4 ones.
So, regroup the tens and ones.
0 tens 4 ones
=  tens 14 ones.

Step:2:
Subtract the tens.
2 tens cannot be subtracted from 0 tens.
So, regroup the hundreds and tens.
7 hundreds 0 tens
= 6 hundreds 9 tens.

Step:3
Subtract the hundreds.

Question 9.
Color the answers from above to find the path to the present.

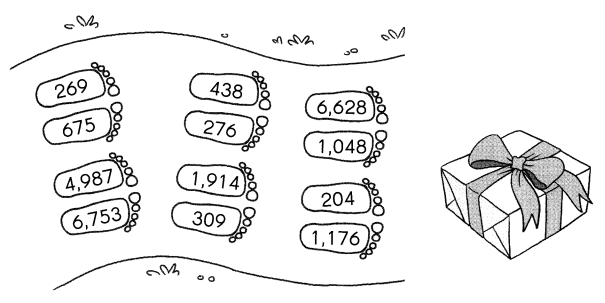
Answer:

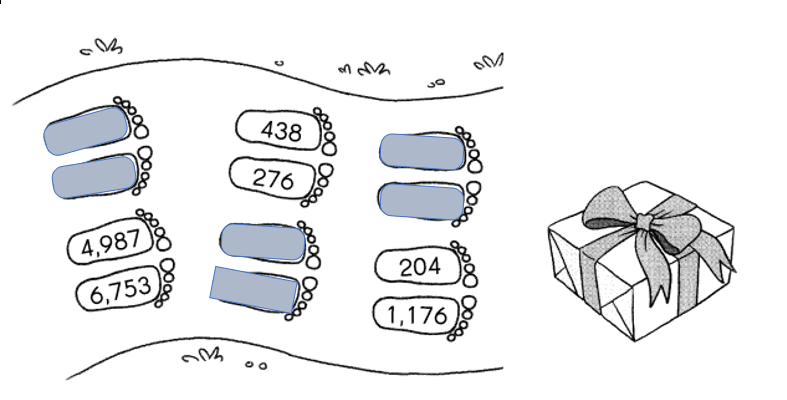
Explanation:
8270 – 1379 = 6891.
4357 – 1789 = 2568.

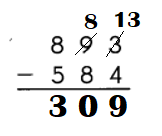
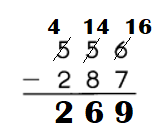
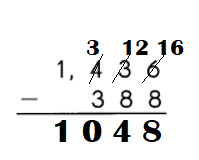
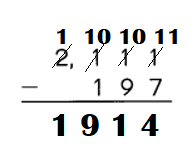
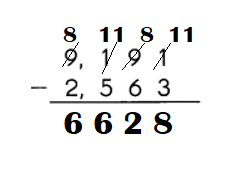
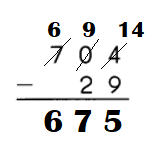
Subtract. Regroup when needed.
Example
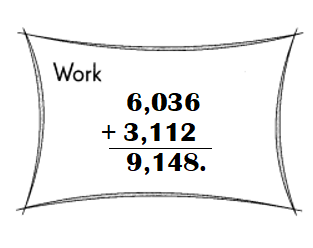
3,852 – 1,621 = 2,231

Question 10.
7,162 – 5,002 = ___
Answer:
7,162 – 5,002 = 2160.

Explanation:
7,162 – 5,002 = 2160.

Question 11.
7,156 – 43 = ___
Answer:
7,156 – 43 = 7113.

Explanation:
7,156 – 43 = 7113.

Question 12.
3,696 – 2,475 = ___
Answer:
3,696 – 2,475 = 1221.

Explanation:
3,696 – 2,475 = 1221.

Question 13.
7,342 – 2,502 = ___
Answer:
7,342 – 2,502 = 4840.

Explanation:
7,342 – 2,502 = 4840.

Question 14.
8,513 – 566 = ___
Answer:
8,513 – 566 = 7947.

Explanation:
8,513 – 566 = 7947.

Question 15.
6,707 – 1,125 = ___
Answer:
6,707 – 1,125 = 5582.

Explanation:
6,707 – 1,125 = 5582.

Question 16.
2,152 – 1,648 = ___
Answer:
2,152 – 1,648 = 504.

Explanation:
2,152 – 1,648 = 504.

Question 17.
5,261 – 85 = ___
Answer:
5,261 – 85 = 5176.

Explanation:
5,261 – 85 = 5176.

Question 18.
9,133 – 7,269 = ___
Answer:
9,133 – 7,269 = 1864.

Explanation:
9,133 – 7,269 = 1864.

Question 19.
3,087 – 1,779 = ___
Answer:
3,087 – 1,779 = 1308.

Explanation:
3,087 – 1,779 = 1308.

Question 20.
7,965 – 978 = ___
Answer:
7,965 – 978 = 6987.

Explanation:
7,965 – 978 = 6987.

Write the corresponding letters from Exercise 11 to 20 to find the name of this national treasure.
Question 21.

Answer:

Explanation:
3,852 – 1,621 = 2,231
7,162 – 5,002 = 2160.
7,156 – 43 = 7113.
3,696 – 2,475 = 1221.
7,342 – 2,502 = 4840.
8,513 – 566 = 7947.
6,707 – 1,125 = 5582.
2,152 – 1,648 = 504.
5,261 – 85 = 5176.
9,133 – 7,269 = 1864.
3,087 – 1,779 = 1308.
7,965 – 978 = 6987.

Question 22.
Where is this national treasure located?
____ __________
Answer:
New York, USA is this national treasure located.

Explanation:
This national treasure is located in New York, USA.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 7 Practice 2 Equivalent Ratios to score better marks in the exam.

Math in Focus Grade 5 Chapter 7 Practice 2 Answer Key Equivalent Ratios

Write ratios to compare the two sets of items.

Question 1.
The ratio of the number of CDs in Group A to the number of CDs in
Group B is ___ : ____
Answer: 4 : 8
Explanation:
Given,
Number of CD’s in Group A is 4,
Number of CD’s in Group B is 8,
So,the ratio of the number of CD’s in Group A to the number of CD’s in Group B is 4 : 8

Question 2.
The ratio of the number of CD-holders in Group A to the number of CD-holders in Group B is ___ : ____
Answer: 1 : 2
Explanation:
Given,
The number of CD – holders in Group A is 1,
The number of CD – holders in Group B is 2,
So the ratio of the number of CD – holders in Group A to the number of CD – holders in Group B is 1 : 2.

Question 3.
____ : ____ = ____ : ____ in simplest form.
Answer: 18 : 12 = 3 : 2
Explanation:
Given,
Both the numbers 18 and 12 can be divisible by 6 we get 3 : 2 to be in the simplest form.

Write ratios to compare the two sets of items.

Question 4.
The ratio of the number of pencils in Group A to the number of pencils in
Group B is ___ : _____
Answer: 18 : 27
Explanation:
In Group A there are 6 bundles of pencils each bundle has 3,
We need to multiply 6 with 3 we get 18,
In Group B there are 9 bundles of pencils each bundle has 3,
We need to multiply 9 with 3 we get 27,
So the ratio of the number of pencils in Group A to the number of pencils in Group B is 18 : 27.

Question 5.
The ratio of the number of bundles in Group A to the number of bundles in
Group B is ___ : ____
Answer: 6 : 9
Explanation:
There are 6 bundles of pencils in Group A,
There are 9 bundles of pencils in Group B,
So the ratio of the number of bundles in Group A to the number of bundles in Group B is 6 : 9.

Question 6.
18 : 27 = 6 : 9 = ___ : ____ in simplest form.
Answer: 2 : 3
Explanation:
Given,
Numbers 18 and 27 are divisible by 3 in the form 6 : 9,
To make it into the simplest form we need to divide by 3, we get 2 : 3.

Find the greatest common factor of each set of numbers.

Example :
4 and 6 2

Question 7.
6 and 9 _______
Answer:
The greatest coomon factor of each set of numbers is 3
Explanation:
Both the numbers 6 and 9 are divisible by 3.

Quantities 8.
6 and 18 _____
Answer: 6
Explanation:
There are four common factors of 6 and 18 that are 1,2, 3 and 6,
So the greatest common factor is 6.

Question 9.
12 and 32 ____
Answer:
4
Explanation:
The greatest common factor for 12 and 32 is 4.

Complete.

Question 10.

Answer: 9: 15

Quantities 11.

Answer: 28:16

Question 12.
4 : 3 = 24 : ___
Answer:24:18

Question 13.
8 : 3 = 64 : ___
Answer: 64:24

Question 14.
4 : 9 = ___ : 45
Answer: 20:45

Question 15.
6 : 7 = 42 : ___
Answer: 42:49

Question 16.
5 : 8 = 45 : ___
Answer: 45:72

Question 17.
9 : 6 = ___ : 54
Answer: 81:54

Complete to express each ratio in simplest form.

Question 18.

Answer: 3:2

Question 19.

Answer: 5:7

Question 20.
12 : 30 = ___ : 5
Answer: 2:5
Both the numbers 12 and 30 need to be divisble by 6 to get the simplest form of 2 : 5

Question 21.
14 : 28 = 1 : ___
Answer: 1:2

Question 22.
60 : 45 = ___ : 3
Answer: Both the numbers 60 and 45 need to be divisble by 15 to get the simplest form of 4 : 3.

Question 23.
72 : 104 = __ : 13
Answer: Both the numbers 72 and 104 need to be divisble by 8 to get the simplest form of 9 : 13.

Question 24.
6 : 16 = __ : __
Answer: Both the numbers 6 and 16 need to be divisble by 2 to get the simplest form of 3 : 8.

Question 25.
15 : 35 = __ : ___
Answer: Both the numbers 15 and 35 need to be divisble by 5 to get the simplest form of 3 : 7.

Question 26.
4 : 48 = ___, ___
Answer: Both the numbers 4 and 48 need to be divisble by 4 to get the simplest form of 1 : 12.

Question 27.
56 : 21 = __ : ___
Answer: Both the numbers 56 and 21 need to be divisble by 7 to get the simplest form of 8 : 3.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 8 Practice 3 Rewriting Decimals as Fractions and Mixed Numbers to score better marks in the exam.

Math in Focus Grade 5 Chapter 8 Practice 3 Answer Key Rewriting Decimals as Fractions and Mixed Numbers

Rewrite each decimal as a fraction or mixed number in simplest form.

Question 1.

Answer:

1.8 in fraction is
1.8 = 9/5

Question 2.

2.2 = ______
Answer:

2.2 in mixed number is 2 × 1/5

Question 3.

Answer:

3.5 mixed number is 3×1/2

Question 4.
0.36
Answer:
0.36 in fraction is 9/25

Question 5.

Answer:

1.35 in mixed number is 1×7/20

Rewrite each decimal as a fraction or mixed number in simplest form.

Question 6.

Answer:

1.12 in mixed number is 1×3/25

Question 7.

Answer:

3.57 in mixed number is 3×57/100

Question 8.

Answer:

0.058 in fraction number is 29/500.

Question 9.

Answer:

0.169 in fraction number is 169/1000.

Question 10.

Answer:

1.092 in mixed number is 1×23/250.

Rewrite the decimal as a mixed number in simplest form.

Question 11.

Answer:

2.235 in mixed number is 2×47/200.

Rewrite each decimal as a fraction or mixed number in simplest form.

Question 12.
7.3
Answer:
7.3 in fraction number is 73/10.

Question 13.
26.9
Answer:
26.9 in mixed number is 269/10.

Question 14.
0.59
Answer:
0.59 in fraction number is 59/100.

Question 15.
15.82
Answer:
15.82 in mixed number is 15×41/50.

Question 16.
1.28
Answer:
1.28 in mixed number is 1×7/25.

Question 17.
4.109
Answer:
4.109 in mixed number is 4109/1000

Question 18.
0.136
Answer:
0.136 in fraction number is 17/125.

Question 19.
3.602
Answer:
3.602 in mixed number is 3×301/500.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 11 Graphs and Probability provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 11 Answer Key Graphs and Probability

Put On Your Thinking Cap!

Challenging Practice

Complete.

Question 1.
The table shows the conversion from gallons to pints. Complete the table.

Answer:

Explanation:
1 gallon = 8 pints
if number of gallons (x) = 1,
number of pints (y) = 1 x 8 = 8
So, substitute the x value and multiply with 8 to complete the table.

Question 2.
Write the equation relating the number of pints (y) to the number of gallons (x).
______________
Answer:
y = x × 8
Explanation:
x – Number of Gallons
y – Number of Pints
y = x × 8

Question 3.
Draw the graph of the equation. Label the axes and the equation.

Answer:

Explanation:
Above graph shows the conversion between pints and gallons.
Take number of gallons on x-axis and number of pints on y-axis.
Take the difference between each pint as 10.

Use the graph to answer the questions.

Question 4.
How many pints is 3\(\frac{1}{2}\) gallons?
Answer:
28 pints
Explanation:
y = 3\(\frac{1}{2}\) × 8 = 28 gallons

Question 5.
How many pints is 4\(\frac{1}{2}\) gallons?
Answer:
36 gallons
Explanation:
y = 4\(\frac{1}{2}\) × 8 = 36 pints

Question 6.
How many gallons is 20 pints?
Answer:
2 \(\frac{1}{2}\) gallons
Explanation:
20 =x × 8 = 28 gallons
x = \(\frac{20}{8}\)
= 2 \(\frac{4}{8}\)

Question 7.
How many gallons is 44 pints?
Answer:
5\(\frac{1}{2}\) gallons
Explanation:
y = x × 8

Complete.

Question 8.
The table shows the conversion from quarts to cups. Complete the table.

Answer:

Explanation:
1 Quarts = 4 cups
if number of Quarts (x) = 1,
number of cups (y) = 1 x 4 = 4
So, substitute the x value and multiply with 4 to complete the table.

Question 9.
Write the equation relating the number of cups (y) to the number of quarts (x).
Answer:
y = x × 4
Explanation:
x is Number of Quarts
y is Number of Cups
y = x × 4

Put On Your Thinking Cap!

Problem Solving

Solve.

Question 1.
Jim has a dime, a nickel, and a quarter. How many different amounts of money can he form using one or more of these coins?
Answer:
These are the possible coins combinations

Explanation:
A probability is a number that reflects the chance or likelihood that a particular event will occur.
So, Jim has the above combinations of coins.

Question 2.
There are an equal number of red, blue, and green beads in a bag. One bead is picked, its color is noted and the bead is replaced. Then a second bead is picked.
a. Draw a tree diagram to show the outcomes.
Answer:

Explanation:
You might observed total 9 combinations as per the above tree diagram.
Now, probability of picking different color beads, is as shown in the diagram.
As we know probability is a number that reflects the chance or likelihood that a particular event will occur.

b. What is the probability of picking two red beads?
Answer:
\(\frac{1}{9}\)
Explanation:
You might observed total 9 combinations as per the above tree diagram.
Now, probability of picking two red beads, is as shown in the diagram below.

c. What is the probability of picking one red and one green bead?
Answer:
\(\frac{2}{9}\)
Explanation:
You might observed total 9 combinations as per the above tree diagram.
Now, probability of picking one red and one green bead, is as shown in the diagram below.

d. What is the probability of picking no red beads?
Answer:
\(\frac{4}{9}\)

Explanation:
You might observed total 9 combinations as per the above tree diagram.
Now, probability of picking no red, means first select blue and green.

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 10 Lesson 10.4 Area of Composite Figures to score better marks in the exam.

Math in Focus Grade 6 Course 1 B Chapter 10 Lesson 10.4 Answer Key Area of Composite Figures

Math in Focus Grade 6 Chapter 10 Lesson 10.4 Guided Practice Answer Key

Use graph paper. Copy the hexagon and solve.

Question 1.
Divide the hexagon into two identical triangles and a rectangle.
Answer:

Explanation:
As shown in the figure, a regular hexagon is divided into two identical traingles and a rectangle.
The two identical traingle are AFE and BCD.
The rectangle formed is ABDE.

Question 2.
Divide the hexagon in another way. Name the polygons that make up the hexagon.

Answer:

Explanation:
Mark the center of the hexagon.
Draw a line from the center point to a vertex.
Draw lines from the center point to the third and fifth vertices.
Each part is a rhombus, which is a four-sided figure with equal side lengths and two sets of parallel sides.
A hexagon can form 3 identical rhombus.

Complete.

Question 3.
Trapezoid ABDE is made up of square A BCE and triangle ECD. triangle ECD is 60 square inches. The length of \(\overline{C D}\) is 12 inches.

a) Find the height of triangle ECD.

Area of triangle ECD = in.²
Area of triangle ECD = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) ∙ ∙ EC
= ∙ EC
÷ = ∙ EC ÷
= EC
The height of triangle ECO is î.. inches,
Answer:
In triangle ECD, the base length is equal to 12 in and the area is 60 sq.in.
Area of triangle ECD = \(\frac{1}{2}\)bh
60 = \(\frac{1}{2}\)×12×EC
60 = 6×EC
60÷6 = 6×EC÷6
10 = EC
The height of triangle ECD is 10 in.

b) Find the area of square ABCE.
Area of square ABCE = l²
=
The area of square ABCE is  square inches.
Answer:
A square has all equal sides, so the length of it will be 10 in.
Area of square ABCE = length×length
= 10×10
= 100 sq.in
The area of square ABCE is 100 sq.in

c) Find the areà of trapezoid ABDE.
Area of the trapezoid ABDE
= area of square ABCE + area of triangle ECD
= +
=  in.²
The area of trapezoid ABDE is square inches.
Answer:
Area of the trapezoid ABDE
= \(\frac{1}{2}\)×(sum of bases)×height
Length of BD = BC+CD = 10+12 = 22 in
= \(\frac{1}{2}\)×(10+22)×10
= \(\frac{1}{2}\)×32×10
= 16×10
= 160 sq.in

Complete.

Question 4.
The area of parallelogram ABEF is 84 square meters.

a) Find the area of triangle BDE.
Area of parallelogram ABEF = bh
= ∙ h
÷ = h ÷
= h
The height of parallelogram ABEF is also the height of triangle BDE.
Area of triangle BDE = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) • BD • h
= \(\frac{1}{2}\) • ( + ) •
= m²
The area of triangle BDE is square meters.
Answer:
Given that area of parallelogram ABEF is 84 sq.m and base is 5m.
Area of parallelogram ABEF = bh
84 = 5×h
84÷5 = 5×h÷5
16.8 = h
The height of parallelogram ABEF is also the height of triangle BDE which is 16.8 m high.
Area of triangle BDE = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) × BD × h
= \(\frac{1}{2}\) × (BC+CD) × h
= \(\frac{1}{2}\) × (12+8) × h
= \(\frac{1}{2}\) × 20 × 16.8
= \(\frac{1}{2}\) × 336
= 168 sq.m

b) Find the area of trapezoid CDEF.
Parallelogram ABEF and trapezoid CDEF have the same height.
Area of trapezoid CDEF = \(\frac{1}{2}\)h(b₁ + b₂)
= • • ( + )
The area of trapezoid CDEF is square meters.
Answer:
Parallelogram ABEF and trapezoid CDEF have the same height. Therefore, the height will be 16.8 m
Since ABEF is a parallelogram, AB and FE will have the same length.
Height = 16.8 m
Sum of bases = 8+5 = 13
Area of trapezoid CDEF = \(\frac{1}{2}\)h(b₁ + b₂)
= \(\frac{1}{2}\)×16.8×13
= \(\frac{1}{2}\)×218.4
= 109.2 sq.m
The area of trapezoid CDEF is 109.2 sq.m.

Math in Focus Course 1B Practice 10.4 Answer Key

Copy each figure and draw straight lines to divide. Describe two ways to find the area of each figure.

Question 1.
Divide the figure into a rectangle and two right triangles.

Answer:

Divide the given figure into two equal parts.
It will form two identical rectangles.
Divide the first identical rectangle diagonally into two equal parts, which will form an equilateral triangle.

Question 2.
Divide the figure into a rectangle and two right triangles.

Answer:

Explanation:
Draw a perpendicular segment between the base and the opposite vertex. Similarly, draw a line segment to the other end also.
The figure is divided now into three parts.
Two parts will form an right angle triangle and the third will form a rectangle.

Question 3.
Divide the figure into a rectangle and a right triangle.

Answer:

Explanation:
Draw a line segment parallel to the base length.
The first part formed is the right angle triangle and the second part is the rectangle.

Copy each figure and draw straight lines to divide. Describe a way to find the area.

Question 4.

Answer:

Explanation:
If the given figure is divided using straight line, it will form a triangle and a rectangle.
Area of polygon will be the sum of areas of rectangle and area of triangle.
Area of polygon = Area of triangle+Area of rectangle
= (\(\frac{1}{2}\) × b × h) + (length×width)
Here, the base of triangle and the width of rectangle will be of same length.

Question 5.

Answer:

Explanation:
If the given figure is divided using straight line, it will form 5 identical triangles.
Area of polygon = n×\(\frac{1}{2}\)×b×h
Here n equals 5
Area of polygon = 5×\(\frac{1}{2}\)×b×h
Here, the base of trinagle will be equal to side length of the pentagon.

Find the area of each figure.

Question 6.
Parallelogram ABDE is made up of square ACDF, triangle ABC, and triangle FDE. Triangle ABC and triangle FDE are identical. The area of square ACDF is 36 square meters. Find the area of triangle ABC. Then find the area of parallelogram ABDE.

Answer:
Given that ACDF is a square and its area is 36 sq.m
Area of ACDF = side×side
36 = side×side
6×6 = side×side
Therefore, side of a sqaure will be 6 m.
Here, the side of square is equal to the height of the trinagle.
The height of triangle is 6m and the base is 4m.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×4×6
= 24÷2
= 12 sq.m
Area of triangle ABC and DFE will be same as both have the same dimensions.
Area of parallelogram ABDE = Area of ABC + Area of DFE + Area of ACDF
= 12+12+36
= 60 sq.m

Question 7.
Math Journal Describe how you would divide the figure with straight lines. Which sides of the figure would you measure to find its area? Explain your answer.

Answer:

Explanation:
Draw a vertical line segment between the two vertex and divide it in two parts.
Two triangles will be formed. Since both the trinagles lie on same base, the base length of these triangles will be same. The perpendicular segment between the base and the opposite vertex will be the height of the triangle.
Measure the drawn line segment to get the base length and the perpendicular line segment to get the height.
Area of triangle can be found using the formula \(\frac{1}{2}\)×b×h.
Area of polygon will be the sum of areas of two trinagles formed.
Area of polygon = Area of first triangle + Area of second trinangle

Find the area of triangle EBC.

Question 8.
In the figure below, trapezoid ABDE is made up of three triangles, and figure ABCE is a parallelogram. Find the area of triangle EBC if the area of trapezoid ABDE is 180 square centimeters.

Answer:
Given that trapezoid ABDE is made up of three triangles, ABE BEC and ECD and its area is 180 sq.cm
Figure ABCE  is a parallelogram.
Area of triangle ECD:
In triangle ECD, the base measures 6cm and the height measures 12cm.
Area of ECD = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×6×12
= 72÷2
= 36 sq.cm
To find the area of triangle EBC, we need the length of BC, which is the base of the parallelogram ABCE.
To calculate the base of parallelogram ABCE , first we need to find the area of ABCE.
Area of trapezoid = Area of parallelogram ABCE + Area of triangle ECD
180 = Area of parallelogram ABCE + 36
180-36 = Area of parallelogram ABCE + 36 – 36
Area of parallelogram ABCE = 144 sq.cm
We know the height of the polygon is 12cm.
Area of parallelogram ABCE = base × height
144 = base × 12
144 ÷ 12 = (base × 12) ÷ 12
12 = base
Thus, the length of BC will be 12 cm.
Area of triangle EBC = \(\frac{1}{2}\)×b×h.
= \(\frac{1}{2}\)×12×12
= 144÷2
= 72 sq.cm

Solve. Use graph paper.

Question 9.
a) Plot the points P (-2, 2), Q (-2, -2), R (-4, -5), S (1, -5), and T (3, -2) on a coordinate plane. Connect the points in order to form figure PQRST.
Answer:
Plot the points P (-2, 2), Q (-2, -2), R (-4, -5), S (1, -5), and T (3, -2) on a coordinate plane.
When connected the points, it forms a polygon as shown below.

b) Find the area of figure PQRST.
Answer:
When the figure PQRST is divided using a line segment. It forms a triangle and a parallelogram.
Area of the polygon PQRST = Area of QTSR + Area of PQT
In the figure, QTSR forms a parallelogram. Let us assume RS as base and the perpendicular segment between the base and the opposite side will be the height.
Base = 5 units
Height = 3 units
Area of QTSR = base×height
= 5×3
= 15 sq.units
In the figure, PQT forms a parallelogram. Let us assume QT as base and the perpendicular segment between the base and the opposite vertex will be the height.
Base = 5 units
Height = 4 units
Area of PQT = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×5×4
= \(\frac{1}{2}\)×20
= 10 sq.units
Area of the polygon PQRST = 15 + 10
= 25 sq.units

c) Point V lies on along \(\overline{Q T}\). The area of triangle PQV is \(\frac{2}{5}\) the area of triangle PQT. Give the coordinates of point V. Plot point V on the coordinate plane.
Answer:
Given that the point V lies on along \(\overline{Q T}\). The area of triangle PQV is \(\frac{2}{5}\) the area of triangle PQT.
Area of PQV = \(\frac{2}{5}\)×area of triangle PQT
As calculated above, Area of PQT = 10 sq.units
= \(\frac{2}{5}\)×10
= 20÷5
= 4 sq.units
Let us assume PQ as base which is 5 units.
Area of PQV = \(\frac{1}{2}\)×b×h
4 = \(\frac{1}{2}\)×4×h
4 = 2×h
4÷2 = (2×h)÷2
2 = h
The height will be 2 units long.
Therefore the point V can be placed 2 units high from the base along \(\overline{Q T}\), which will be (0,-2)

Find the area of trapezoid MNRS.

Question 10.
In the figure below, trapezoid MNRS is made up of trapezoid MNPT, triangle TPQ, and parallelogram TQRS. The area of triangle TPQ is 84 square feet. The lengths of \(\overline{N P}\), \(\overline{P Q}\), and \(\overline{Q R}\) are in the ratio 2 : 1.5 : 1.
Find the area of trapezoid MNRS.

Answer:
Given that the trapezoid MNRS made up of trapezoid MNPT, triangle TPQ, and parallelogram TQRS.
Area of triangle TPQ = 84 sq.ft and the length of PQ is 12 ft and MS is 18 ft.
Area of TPQ = \(\frac{1}{2}\)×b×h, where b is length of PQ and h is unknown.
84 = \(\frac{1}{2}\)×12×h
84 = 6×h
84÷6 = (6×h)÷h
14 = h
The height of triangle will be 14 ft.
The lengths of \(\overline{N P}\), \(\overline{P Q}\), and \(\overline{Q R}\) are in the ratio 2 : 1.5 : 1
Let p be the proportion.
1.5p=12
1.5p÷1.5 = 12÷1.5
p = 8
Length of NP = 2p = 2×8 = 16 ft
Length of QR = 1p = 1×8 = 8 ft
NR = NP+PQ+QR
= 16+12+8
= 36 ft
In trapezoid MNRS, MS and NR will be the two parallel bases.
Area of trapezoid MNRS = \(\frac{1}{2}\)×(sum of bases)×height
= \(\frac{1}{2}\)×(18+36)×14
= \(\frac{1}{2}\)×54×14
= 756÷2
= 378 sq.ft
Thus, the area of trapezoid MNRS = 378 sq.ft

Find the area of triangle BDE.

Question 11.
The figure below is made up of two trapezoids ABEFand BCDE. The area of triangle FGE is 26 square inches, and the area of trapezoid BCDE is 82.5 square inches. BG is equal to GE. Find the area of triangle BDE.

Answer:
The figure is made up of two trapezoids ABEFand BCDE, two triangles FGE,BCD and BDE.
Area of triangle FGE is 26 sq.in and height is 8 in.
Area of trapezoid BCDE is 82.5 sq.in
BG is equal to GE and length of CD is 2 in.
First we need to find the base length, GE.
Area of triangle FGE = \(\frac{1}{2}\)×base×height
26 = \(\frac{1}{2}\)×base×8
26 = 4×base
26÷4 = (4×base)÷4
6.5 = base
Length of GE = Length of BG = 6.5 in
Length of BE = Length of GE + Length of BG
= 6.5+6.5 =13 in
Area of trapezoid BCDE = \(\frac{1}{2}\)×(sum of bases)×height
82.5  =  \(\frac{1}{2}\)×(BE+CD)×height
82.5  =  \(\frac{1}{2}\)×15×height
82.5 = 7.5×height
82.5÷7.5 = (7.5×height)÷7.5
height = 11 in
The height of tarpezoid and triangle will be of same length.
Now, we can find the area of triangle BDE.
Area of triangle BDE = \(\frac{1}{2}\)×base×height
= \(\frac{1}{2}\)×BE×height
= \(\frac{1}{2}\)×BE×height
= \(\frac{1}{2}\)×13×11
= 143÷2
= 71.5 sq.in

Find the area of the shaded region.

Question 12.
\(\frac{3}{8}\) of the triangle is shaded.

Answer:
Given trinagle is 28cm wide and 35cm high.
Area of trinagle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 28 × 35
= \(\frac{1}{2}\) × 980
= 980÷2
= 490 sq.cm
The shaded region is \(\frac{3}{8}\) of the triangle.
Therefore, area of shaded region will be \(\frac{3}{8}\) × 490
= 1470÷8
= 183.75 sq.cm

Find the height of trapezoid PQRS.

Question 13.
Trapezoid PORS s made up of isosceles triangle PQS and triangle SQR. The area of triangle PQS is 16.5 square inches. The areas of triangle PQS and triangle SQR are in the ratio 2 : 3, Find the height of trapezoid PQRS.

Answer:
Given that the trapezoid PORS s made up of isosceles triangle PQS and triangle SQR.
Area of triangle PQS is 16.5 square inches.
Since PQS is an isosceles triangle, PS will be equal to SQ.
The areas of triangle PQS and triangle SQR are in the ratio 2 : 3.
\(\frac{PQS}{SQR}\) = \(\frac{2}{3}\)
3×PQS = 2×SQR
3×16.5 = 2×SQR
49.5 = 2×SQR
49.5÷2 = (2×SQR)÷2
24.7 = SQR
Area of triangle SQR = 24.7 sq.in
Area of trapezoid = Area of triangle PQS + Area of triangle SQR
= 16.5+24.7
= 41.2 sq.in
Area of trapezoid = \(\frac{1}{2}\)×(sum of bases)×height
41.2 = \(\frac{1}{2}\)×(6+9)×height
41.2 = \(\frac{1}{2}\)× 15 ×height
41.2 = 7.5×height
41.2 ÷ 7.5 = (7.5×height)÷7.5
5.4= height
Thus, the height of trapezoid PQRS = 5.4 in

Find the area of each figure.

Question 14.
In the figure below, trapezoid ABCD is made up of square BCDE and triangles ABF and APE. The area of square BCDE is 576 square feet. The ratio of BF to FE is 2: 1. Find the area of triangle ABF.

Answer:
Given that the trapezoid ABCD is made up of square BCDE and triangles ABF and APE.
Area of square BCDE = 576 sq.ft
Area of square BCDE = length×length
576 = length×length
24×24 = length×length
Length of square = 24 ft.
The ratio of BF to FE is 2: 1.
\(\frac{BF}{FE}\) = \(\frac{2}{1}\)
1×BF = 2×FE
BE = 2×FE + FE
24 = 3×FE
24÷3 = 3×FE÷3
FE = 8ft
BF = 2×8 = 16ft
Area of triangle ABF = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 16 × 12
= 192÷2
= 96 sq.ft

Brain @ Work

Question 1.
Figure ABCD is made up of square PQRS and four identical triangles. The area of triangle APD
is 49 square feet. The lengths of \(\overline{\mathrm{AP}}\) and \(\overline{\mathrm{PD}}\) are in the ratio 1: 2. Find the area of figure ABCD.

Answer:
Given that the figure ABCD is made up of square PQRS and four identical triangles. The area of triangle APD
is 49 square feet.
The lengths of \(\overline{\mathrm{AP}}\) and \(\overline{\mathrm{PD}}\) are in the ratio 1: 2.
Let the proportion be ‘p’
\(\frac{AP}{PD}\) = 1: 2
PD = 2×AP
Area of triangle APD = \(\frac{1}{2}\) × base × height
49 = \(\frac{1}{2}\) × PD × AP
49 = \(\frac{1}{2}\) × 2×AP×AP
49 = AP×AP
7×7 = AP×AP
AP = 7ft
PD = 2×7 = 14ft
As all are identical triangles, the longest side or base will be twice of the height.
SC = 2×DS, where DS = 7ft
PD = PS+SD
14 = PS+7
14-7 = PS+7-7
PS = 7ft
PQRS is a square, so all sides will be equal.
Area of square PQRS = length×length
= 7×7
= 49 sq.ft
Area of ABCD = Area of four identical triangles + Area of square PQRS
= 4×49 + 49
= 196+49
= 245 sq.ft

Question 2.
The figure is made up of squares BCDE and AEFH. The length of \(\overline{D E}\) is 6 centimeters, and the length of \(\overline{E F}\) is 12 centimeters.
a) Write the length of \(\overline{F G}\) in terms of x.
Answer:
Length of DE = 6 cm
Length of EF = 12 cm
Since AEFH is a square, all sides will be equal.
Therefore, the length of HF will be 12cm
HF = HG + GF
12 = x+GF
12-x = x+GF-x
GF = 12-x
Therefore, the length of \(\overline{F G}\) will be 12-x

b) Find the area of the shaded region in terms of x.
Answer:

c) Give the value of x for which the shaded region has the greatest area. What is the shape of the shaded region for the value of x you have given?

Answer:

Question 3.
Figure ABCD is a square. Point S is in the middle of \(\overline{A D}\), and point T is in the middle of and \(\overline{C D}\). What fraction of the square is shaded?

Answer:
Given that the figure ABCD is a square.
Point S is in the middle of \(\overline{A D}\), and point T is in the middle of and \(\overline{C D}\).
To find the fraction of shaded square we need to find the area of trinagle STB.
Let us assume each side length of the square as 1m.
AD=DC=CB=BA=1m
Since S and T are the midpoints of AD and DC.
Length of DS = Length of SA = \(\frac{1}{2}\) m
Length of DT = Length of TC = \(\frac{1}{2}\) m
ASB forms a right angle triangle; AB²+AS² = SB²
1²+(\(\frac{1}{2}\))² = SB²
1+\(\frac{1}{4}\) = SB²
\(\frac{5}{4}\) = SB²
SB = √\(\frac{5}{4}\)
SB = \(\frac{√5}{2}\)
In triangle DST
ST²=(\(\frac{1}{2}\))² + (\(\frac{1}{2}\))²
= \(\frac{1}{4}\) + \(\frac{1}{4}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
ST = √\(\frac{1}{2}\)
Draw a perpendicular segment from BU on ST

Now BUS will be a right angle triangle,
BS²=BU²+US²
Length of SU will be \(\frac{1}{2}\) of ST
Length of SU = \(\frac{1}{2}\) × \(\frac{1}{√2}\) = \(\frac{1}{2√2}\)
(\(\frac{√5}{2}\))² = BU²+ (\(\frac{1}{2√2}\) )²
\(\frac{5}{4}\) = BU²+\(\frac{1}{8}\)
\(\frac{5}{4}\)–\(\frac{1}{8}\) = BU²
(\(\frac{5}{4}\)×\(\frac{2}{2}\))-\(\frac{1}{8}\) = BU²
\(\frac{10}{8}\)–\(\frac{1}{8}\) = BU²
\(\frac{9}{8}\)= BU²
BU=√\(\frac{9}{8}\)
BU=\(\frac{3}{2√2}\)
Area of STB:
Length of ST=\(\frac{1}{√2}\)
Height = \(\frac{3}{2√2}\)
Area of triangle STB=\(\frac{1}{2}\)×b×h
=\(\frac{1}{2}\)×\(\frac{1}{√2}\)×\(\frac{3}{2√2}\)
= 2×√2×2√2
= 2×2×2=8(√2×√2=2)
= \(\frac{3}{8}\) sq.m

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 10 Review Test to score better marks in the exam.

Math in Focus Grade 6 Course 1 B Chapter 10 Review Test Answer Key

Concepts and Skills

Identify a base and a height of each triangle.

Question 1.

Answer:
Assume a side as the base of triangle and the perpendicular segment between the base and the opposite vertex will be the height of the triangle.
Let us assume the side BC as the base, then the segment AD which is drawn perpendicular between the base and the opposite vertex will be the height.
Thus, base of triangle = BC
Height of the triangle = AD.

Question 2.

Answer:
Assume a side as the base of triangle and the perpendicular segment between the base and the opposite vertex will be the height of the triangle.
Let us assume the side NP as the base, then the segment MQ which is drawn perpendicular between the base and the opposite vertex will be the height.
Thus, base of triangle = NP
Height of the triangle = MQ

Find the area of each figure.

Question 3.

Answer:
If we assume the line segment measuring 28cm as the base, then the height will be the perpendicular line segment between the base and the opposite vertex which is 8cm.
Area of triangle = \(\frac{1}{2}\)×28×8
= \(\frac{1}{2}\)×224
= 224÷2
= 112 sq.cm
Thus, the area for the given polygon will be 112 sq.cm

Question 4.

Answer:
The given polygon is parallelogram.
Let us assume the base of the parallelogram as 46.3 cm, then the height will be the perpendicular line segment between the base and the opposite vertex which is 15 cm.
Area of parallelogram = base×height
= 46.3×15
= 694.5 sq.cm
Thus, the area for the given polygon will be 694.5 sq.cm

Question 5.

Answer:
The given polygon is similar to trapezium.
A trapezium has a pair of parallel sides, measuring 50cm and 18cm.
The height will be the perpendicular line segment between the base and the opposite vertex which is 31.5 cm.
Area of trapezoid = \(\frac{1}{2}\)×(sum of bases)×height
= \(\frac{1}{2}\)×(50+18)×31.5
= \(\frac{1}{2}\)×68×31.5
= 2142÷2
= 1071 sq.cm
Thus, the area for the given polygon will be 1071 sq.cm

Find the area of the shaded region.

Question 6.
The area of the regular octagon below is 560 square inches.

Answer:
A regular octagon will be made up of her 8 identical triangles.
Thus, the area of octagon will be equal to sum of the 8 identical triangles.
Given that the area of the regular octagon is 560 sq.in
Area of octagon = 8 × Area of triangle
560 = 8 × Area of triangle
560÷8 = (8 × Area of triangle)÷8
Area of triangle = 70sq.in
The shaded region is half of the triangle.
Area of shaded region = \(\frac{1}{2}\)×Area of triangle
= \(\frac{1}{2}\)×70
= 35 sq.in
Thus, the area of shaded region is 35 sq.in

Problem Solving

Find the area of the shaded region.

Question 7.

Answer:
The given figure has two triangles and a square.
Length of square is 15 cm.
Area of square will be length×length
= 15×15
= 225 sq.cm
The area of shaded region can be calculated by subtracting the area of square from the area of parallelogram.
So, calculate the area of parallelogram.
Area of parallelogram = base×height
The base of parallelogram is 15+20=35 cm and
the height will be 15 cm.
= 35×15
= 525 sq.cm
Area of shaded region = Area of parallelogram – Area of square
= 525 – 225
= 300 sq.cm

Solve.

Question 8.
Figure ABCD is a parallelogram. BC is 16 centimeters, CD is 12 centimeters, and AH is 10 centimeters.
a) Find the area of parallelogram ABCD.
Answer:
Given that figure ABCD is a parallelogram.
BC is 16 centimeters and AH is 10 centimeters.
Area of parallelogram ABCD = base × height
= BC × AH
= 16×10
= 160 sq.cm

b) Find the length of \(\overline{\mathrm{AK}}\). Round your answer to the nearest tenth of a centimeter.

Answer:
ABCD is a parallelogram with two triangles ABC and ACD.
Area of parallelogram = Area of triangle ABC + Area of triangle ACD
The area of parallelogram is 160 sq.cm
Area of triangle ABC= \(\frac{1}{2}\)×base×height
= \(\frac{1}{2}\)×BC×AH
= \(\frac{1}{2}\)×16×10
= 160÷2
= 80 sq.cm
Area of parallelogram = 80 + Area of triangle ACD
160 = 80 + Area of triangle ACD
160-80 = 80 + Area of triangle ACD – 80
80 = Area of triangle ACD
Length of AD = 12cm
Area of triangle ACD = \(\frac{1}{2}\)×base×height
80 = \(\frac{1}{2}\)×12×AK
80 = 6×AK
80÷6 = (6×AK)÷6
13.3 = AK
13.3 when rounded of to nearest tenth will be 13
The length of AK = 13cm

Question 9.
Figure ABCD is a trapezoid. The length of \(\overline{\mathrm{BC}}\) is 36 centimeters. The areas of triangles ABC and ACD are in the ratio 1.5:1. Find the length of \(\overline{\mathrm{AD}}\).

Answer:
Given that figure ABCD is a trapezoid.
The length of \(\overline{\mathrm{BC}}\) is 36 centimeters.
Area of triangle ABC = \(\frac{1}{2}\)×base×height
= \(\frac{1}{2}\)×36×10
= 360÷2
= 180 sq.cm
The areas of triangles ABC and ACD are in the ratio 1.5:1
\(\frac{ABC}{ACD}\) = \(\frac{1.5}{1}\)
Area of triangle ABC = 1.5×Area of triangle ACD
180 = 1.5×Area of triangle ACD
180÷1.5 = (1.5×Area of triangle ACD)÷1.5
120 = Area of triangle ACD
Area of triangle ACD = \(\frac{1}{2}\)×base×height
120 = \(\frac{1}{2}\)×AD×10
120 = AD×5
120 ÷ 5  = (AD×5)÷5
24 = AD
Thus, the length of \(\overline{\mathrm{AD}}\) is 24 cm.

Question 10.
Parallelogram PRTVis made up of triangle PQV, triangle QUV, and trapezoid QRTU. The area of parallelogram PRTV is 96 square feet. The lengths of \(\overline{\mathrm{TU}}\) and \(\overline{\mathrm{UV}}\) are equal. Find the area of triangle QUV.

Answer:
Parallelogram PRTV is made up of triangle PQV, triangle QUV, and trapezoid QRTU.
The area of parallelogram PRTV is 96 sq.ft. The lengths of TU is equal to UV.
Area of parallelogram PRTV = 96
Area of parallelogram PRTV = base×height
96 = base×8
96÷8 = (base×8)÷8
12 = base
TV is the base of the parallelogram PRTV which is equal to 12 ft.
TV = VU+UT
12 = VU+VU
12 = 2×VU
12÷2 = (2×VU)÷2
6 = VU
Length of VU is 6 ft.
Area of triangle QUV = \(\frac{1}{2}\)×base×height
= \(\frac{1}{2}\)×UV×8
= \(\frac{1}{2}\)×6×8
= 48÷2
= 24 ft

Question 11.
Charles drew a regular hexagon and divided it into two identical trapezoids. The side length of the hexagon is 16 centimeters, and the length of the diagonal shown is 32 centimeters. Charles measured the height of one of the trapezoids and found that the height was 13.9 centimeters. Find the area of the hexagon.

Answer:
A regular hexagon and divided it into two identical trapezoids.
The side length of the hexagon is 16 cm and the height of one of the trapezoids is 13.9 cm. The length of the diagonal shown is 32 cm.
The side length makes with the height of the trapezium.
Pythagoras theorem is applied to get the base of the triangle.
base² = 16²-(13.9)²
base² = 256-193.21
base² = 62.79
base will be the square root of 62.79
Base length will be 7.9 cm
The length of opposite diagonal can be calculated by subtracting the sum of base length of two triangle from the length of diagonal.
Length of the parallel side = 32-(7.9+7.9)
= 16.2 cm
Area of trapezoid = \(\frac{1}{2}\)×(sum of bases)×height
= \(\frac{1}{2}\)×(32+16.2)×13.9
= \(\frac{1}{2}\)×48.2×13.9
= \(\frac{1}{2}\)×669.9
= 334.9 sq.cm
Area of hexagon = Area of trapezoid + Area of trapezoid
= 334.9+334.9
= 669.8 sq.ft
Thus, the area of hexagon is 669.8 sq.ft