Hillary

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 8 Practice 3 Ways to Add to score better marks in the exam.

Math in Focus Grade 1 Chapter 8 Practice 3 Answer Key Ways to Add

Complete each addition sentence.

Example
What is double 1?

Double 1 means to add 1 more to 1.
1 + 1 = 2

Question 1.
What is double 2?

Double 2 means to add ___ more to 2.
___ + ___ = ____
Answer:
Double 2 means to add 2 more to 2.
2 + 2 = 4

Question 2.
What is double 3?

Double 3 means to add ___ more to 3.
____ + ___ = ___
Answer:
Double 3 means to add 3 more to 3.
3 + 3 = 6

Question 3.
4 + 4 = ____
Answer: 8

Question 4.
5 + 5 = ____
Answer: 10

Complete each addition sentence.

Question 5.
a. 3 + 3 = ____
3 + 4 = ____
Answer:
3 + 3 = 6
3 + 4 = 7

b. 3 + 3 is double ____
3 + 4 is double ____ plus ____
Answer:
3 + 3 is double 6
3 + 4 is double 6 plus 1

Complete the number bonds. Then fill in the blanks.

Example

Question 6.

Answer:

Question 7.

Answer:

Use doubles facts to complete the addition sentences.

Example

Question 8.

Answer: 0 + 0 = 0

Question 9.

Answer: 6 + 6 = 12

Question 10.

Answer: 5 + 5 = 10

Question 11.

Answer: 8 + 8 = 16

Question 12.

Answer: 9 + 9 = 18

Question 13.

Answer: 10 + 10 = 20

Add the doubles-plus one numbers. Use doubles facts to help you. Then write the doubles fact you used.

Example
5 + 6 = 11
Doubles fact: 5 + 5 = 10

Question 14.
7 + 6 = ____
Doubles fact: ___ + ____ = _____
Answer:
7 + 6 = 13
Doubles fact: 6 + 6 = 12

Question 15.
7 + 8 = ____
Doubles fact: ___ + ____
Answer:
7 + 8 = 15
Doubles fact: 7 + 7 = 14

Question 16.
9 + 10 = ____
Doubles fact: ___ + ____
Answer:
9 + 10 = 19
Doubles fact: 9 + 9 = 18

Question 17.
8 + 9 = ____
Doubles fact: ___ + ____
Answer:
8 + 9 = 17
Doubles fact: 8 + 8 = 16

Read More:

Apollohosp Pivot Calculator

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 6 Practice 1 Finding the Area of a Rectangle with Fractional Side Lengths to score better marks in the exam.

Math in Focus Grade 5 Chapter 6 Practice 1 Answer Key Finding the Area of a Rectangle with Fractional Side Lengths

Example

Question 1.

A = ____ × width
= ____ × \(\frac{1}{2}\)
= ___ m²
The area of the rectangle is ____ square meters.
Answer:
Area = length × width
A = 3/5 × 1/2
A = 3/10 m²
Explanation:
In the above image we can observe that length is 3/5 m and width is 1/2 m. The area of the rectangle is 3/10 square meters.

Question 2.

Answer:
Area = length × width
A = 3/4 × 1/8
A = 3/32 ft²
Explanation:
In the above image we can observe that length is 3/4 feet and width is 1/8 feet. The area of the rectangle is 3/32 square feet.

Find the area of each rectangle.

Question 3.

Answer:
Area = length × width
A = 4/5 × 5/6
A = 2/3 cm²
Explanation:
In the above image we can observe that length is 4/5 cm and width is 5/6 cm. The area of the rectangle is 2/3 square centimeters.

Question 4.

Answer:
Area = length × width
A = 3/7 × 2/4
A = 3/14 m²
Explanation:
In the above image we can observe that length is 3/7 m and width is 2/4 m. The area of the rectangle is 3/14 square meters.

Question 5.
A 1 -meter square plot of land is covered by a rectangular patch of grass that measures \(\frac{4}{7}\) meter by \(\frac{2}{3}\) meter. What is the area of the patch of grass?

Answer:
Area = length × width
A = 4/7 × 2/3
A =8/21 m²
Explanation:
In the above image we can observe that length is 4/7 m and width is 2/3 m. The area of the rectangular patch of grass is 8/21 square meters.

Question 6.
Find the area of the top of a rectangle bedside table with a length of \(\frac{3}{4}\) yard and width that is \(\frac{1}{6}\) yard less than the length.
Answer:
Length = 3/4 yard
width = (3/4 – 1/6) yard
= 7/12 yard
Area = length × width
A = 3/4× 7/12
A = 7/16 yard²
Explanation:
The area of the top of a rectangle bedside table with a length of 3/4 yard and width of 7/12 yard is 7/16 square yards.

Find the area of each composite figure.

Question 7.

Answer:

Area of the rectangle = length ×  width
A = (3/5 ×  1/5) + (3/5 ×  1/5)
A = 3/25 + 3/25
A = 6/25 cm²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length and width of first rectangle are 3/5 cm and 1/5 cm.
So, Area of first rectangle = 3/5 × 1/5 = 3/25 cm²
Length of second rectangle is 3/5 cm (4/5 – 1/5 ) and width is 1/5 cm.
So, Area of second rectangle = 3/5 × 1/5 = 3/25 cm²
Hence, total area of the image = 3/25 + 3/25 = 6/25 cm²
Question 8.

Answer:

Explanation:
Area of the rectangle = length ×  width
A = (3/9 ×  2/7) + (4/7 ×  1/9)
A = 6/63 + 4/63
A = 10/63 m²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length of first rectangle is 3/9 m (4/9 – 1/9 ) and width is 2/7 m.
So, Area of first rectangle = 3/9 × 2/7 = 6/63 m²
Length and width of second rectangle are 4/7 m and 1/9 m.
So, Area of second rectangle =4/7 × 1/9 = 4/63 m²
Hence, total area of the image = 6/63 + 4/63 = 10/63 m²

Question 9.

Answer:

Area of the rectangle = length ×  width
A = (4/5 ×  3/5) + (1/10×  1/5)
A = 12/25 + 1/50
A = (24 + 1)/ 50
A = 1/2 m²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length of first rectangle is 4/5 m and width is 3/5 m.
So, Area of first rectangle = 4/5 × 3/5 = 12/25 m²
Length and width of second rectangle are 1/10 m and 1/5 m.
So, Area of second rectangle = 1/10 × 1/5 = 1/50 m²
Hence, total area of the image = 12/25+ 1/50 = (24 + 1)/50 = 1/2 m²

Question 10.

Answer:

Area of the rectangle = length ×  width
A = (6/7 ×  1/3) + (4/7 ×  2/9) + (2/7 ×  2/9)
A = 2/7 + 8/63 + 4/63
A = (18 + 8 + 4)/63
A = 30/63 Yd²
Explanation:
To calculate the area we have divided the image into three rectangles.
Length and width of first rectangle are 6/7 yard and 1/3 yard.
So, Area of first rectangle =6/7 × 1/3 = 2/7 yd²
Length and width of second rectangle are 4/7 yard and 2/9 yard.
So, Area of second rectangle = 4/7 × 2/9 = 8/63 yd²
Length of third rectangle is 2/7 yard and width is 2/9 yard.
So, Area of third rectangle = 2/7 × 2/9 = 4/63 yd²
Hence, total area of the image = 2/7 + 8/63 + 4/63 = 30/63 yd²

Find the area of the shaded part.

Question 11.

Answer:
Area of the square = length ×  width
A = (3/5 ×  3/5) – (1/5 × 1/5)
A = 9/25 – 1/25
A = 8/25 in²
Explanation:
To calculate the area we have subtract inner square from outer square.
Length and width of outer square are 3/5 in and 3/5 in.
So, Area of outer square = 3/5 × 3/5 = 9/25 in²
Length and width of inner square are 1/5 in and 1/5 in.
So, Area of inner square = 1/5 × 1/5 = 1/25 in²
Hence, area of the shaded part = 9/25 – 1/25 = 8/25 in²

Question 12.

Answer:
Area of the rectangle = length ×  width
A = (8/9 × 2/3) – (5/9 × 1/6)
A = 16/27 – 5/54
A = (32 – 5)/54
A = 1/2 m²
Explanation:
To calculate the area we have subtract inner rectangle from outer rectangle.
Length and width of outer rectangle are 8/9 m and 2/3 m.
So, Area of outer rectangle =8/9 × 2/3 = 16/27 m²
Length and width of inner rectangle are 5/9 m and 1/6 m.
So, Area of inner rectangle = 5/9 × 1/6 = 5/54 m²
Hence, area of the shaded part = 16/27 – 5/54 = 27/54 = 1/2m²

Read More:

Easy Pivot Point Calculator

This handy Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 14 and 15 provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Cumulative Review Answer Key for Chapters 14 and 15

Concepts and Skills

Name each solid. Then write the number of faces and vertices, and the shapes of the faces. (Lesson 14.1)

Question 1.

Answer:

Explanation:
Given solid triangular prism shape has  number of faces -4,
number of vertices-6 and shapes of faces- 8.

Question 2.

Answer:

Explanation:
Given solid triangular prism shape has  number of faces – 5,
number of vertices – 5 and shapes of faces – 10.

Name the solid formed from each net. (Lesson 14.1)

Question 3.

Answer:

Explanation:
Given solid formed with the net is pentagonal prism.

Question 4.

Answer:

Explanation:
Given solid formed with the net is square based pyramid.

Complete. (Lesson 14.2)

Question 5.
A ___ has two parallel and congruent bases that are joined by a curved surface.
Answer:
Cylinder,

Explanation:
A cylinder is formed by two parallel congurent circular bases and a curved surface that connects
the bases.

Question 6.
A ____ does not have any edges or vertices, and has the same distance
across any line through its center.
Answer:
Circle,

Explanation:
A circle does not have any edges or vertices, and has the same distance
across any line through its center.

Question 7.
A _____________ has one vertex, a circular base, and a curved surface.
Answer:
Cone,

Explanation:
A cone has one vertex, a circular base, and a curved surface.

Question 8.
A sphere has no ___ and________ surfaces.
Answer:
Faces, Edges, Vertices,

Explanation:
A sphere has no faces, edges, vertices and surfaces.

Find how many unit cubes are used to build each solid. (Lesson 15.1)

Question 9.

_____________ unit cubes
Answer:
16 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 16 unit cubes,
So, the volume of a 16 unit cubes = 16 X (Side × Side × Side),
= 16 X (1 unit × 1 unit × 1 unit),
= 16 unit cubes.

Question 10.

_____________ unit cubes
Answer:
13 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 13 unit cubes,
So, the volume of a 13 unit cubes = 13 X (Side × Side × Side),
=13 X (1 unit × 1 unit × 1 unit),
= 13 unit cubes.

Draw a cube with edges 2 times as long as the edges of this unit cube. (Lesson 15.2)

Question 11.

Answer:

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
Shown the volume of a unit cube = Side × Side × Side,
= 2 units × 1 unit × 1 unit,
= 2 units cubes.

Complete the drawing of this rectangular prism. (Lesson 15.2)

Question 12.

Answer:

Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 4 units X 2 units  X 3 units =
24 unit cubes rectangular prism.

Find the surface area of each prism. (Lesson 15.3)

Question 13.

Answer:
The surface area of rectangular prism is 1860 cm²,

Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(18 cm X 20 cm) + (20 cm X 15 m) + (15 cm X  18 cm)],
= 2 X [(360 cm²) + (300 cm²) + (270 cm²)]
= 2 X [ 930 cm²],
= 1860 cm².

Question 14.

Answer:
Surface area of triangular prism = 1,392 cm²,

Explanation:
2 × \(\frac{1}{2}\) × 12 cm × 16 cm = 192 cm²,
12 cm × 25 cm = 300 cm.²
16 cm × 25 cm = 400 cm.²
20 cm × 25 cm = 500 cm.²
192 cm ²+   300 cm² + 400 cm² + 500 cm.² = 1,392 cm²,
Surface area of triangular prism = 1,392 cm².

These solids are built using 1-inch cubes. Find and compare their volumes. (Lesson 15.4)

Question 15.

Length = _____4_______ in.
Width = _____4_______ in.
Height = _____4______ in.
Volume = _____64_____ in.³

Length = ______6______ in.
Width = _______4_____ in.
Height = ______3_____ in.
Volume = _____72_____ in.³
Solid _______A____ has less volume than solid ____B______.
Answer:
Volume of given cube A has  64 cubic units,
Volume of given cube B has  72 cubic units,
Solid A has less volume than solid B,

Explanation:
As we know volume of  solid is l X w X h,
Total surface area of A is 4 in X 4 in X 4 in = 64 cubic units.
Total surface area has 6 in X 4 in X 3 in = 72 cubic units.
Given cube contains 2 less small unit cubes so first we
calculate total surface and subtract missing cubic uints,
therefore, Solid A has less volume than solid B,

Find the volume of each rectangular prism. (Lesson 15.5)

Question 16.

Answer:
Volume of given rectangular prism is 27 cm³,

Explanation:
Given Length = 3 cm, Width = 1 cm and Height = 9 cm,
Volume of the rectangular prism is lwh = 3 cm X 1 cm X 9 cm = 27 cm³.

Question 17.

Answer:
Volume of given rectangular prism is 330 m³,

Explanation:
Given Length = 11 m, Width = 6 m and Height =5 m,
Volume of the rectangular prism is lwh = 11 cm X 6 m X 5 m = 330 m³.

Find the volume of water in each container in liters and milliliters. (Lesson 15.5)

Question 18.

Answer:
Volume of given rectangular prism is 10,290 cm³ which is equal to 10,290 milliliters,

Explanation:
Given Length = 14 cm, Width = 21 cm and Height = 35 cm,
Volume of the rectangular prism is lwh = 14 cm X 21 cm X 35 cm = 10,290 cm³.
as 1 cubic centimeter is equal to 1 milliliters therefore volume of given
rectangular prism is 10,290 cm³ which is equal to 10,290 milliliters.

Question 19.

Answer:
Volume of given rectangular prism is 1,008 cm³ which is equal to 1,008 milliliters,

Explanation:
Given Length = 7 cm, Width = 9 cm and Height = 16 cm,
Volume of the rectangular prism is lwh = 7 cm X 9 cm X 16 cm = 1,008 cm³.
as 1 cubic centimeter is equal to 1 milliliters therefore volume of given
rectangular prism is 1,008 cm³ which is equal to 1,008 milliliters.

Problem Solving

Solve. Show your work.

Question 20.
The length of a rectangular block is 20 inches. Its width is half its length.
Its height is half its width. What is the surface area of the block?
Answer:
The surface area of a rectangular prism is 1860 cm²,

Explanation:
Given the length of a rectangular block is 20 inches. Its width is half its length.
So width is 10 inches, Its height is half  its width is 5 inches
The surface area of the block is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(10 in X 20 in) + (5 in X 20 in) + (5 in X  10 in)],
= 2 X [(200 in²) + (100 in²) + (50 in²)]
= 2 X [ 350 in²],
= 700 in².

Solve. Show your work.

Question 21.
A rectangular piece of poster board measures 70 centimeters by 50 centimeters.
The net of a cube with 12-centimeter edges is cut from it.
What is the area of the poster board left?
Answer:
The area of the poster board left 2,636 cm²,
Explanation:
Given a rectangular piece of poster board measures 70 centimeters by 50 centimeters,
70 cm X 50 cm = 3,500 cm², The net of a cube with 12-centimeter edges is cut from it.
Volume of cube is 6 X 12 cm X 12 cm = 864 cm², therefore the area of the poster board
left is 3,500 cm² – 864 cm² = 2,636 cm².

Question 22.
A rectangular prism is 15 inches long and 12 inches high.
Its width is \(\frac{3}{5}\) its length. Find its volume.
Answer:
Volume of a rectangular prism is 1,620 in³,

Explanation:
Given a rectangular prism is 15 inches long and 12 inches high.
Its width is \(\frac{3}{5}\) its length. So length is
\(\frac{3}{5}\) X 15 = \(\frac{3 X 15}{5}\) = 9 inches,
therefore volume is 15 inches X 12 inches X 9 inches = 1,620 in³.

Solve. Show your work.

Question 23.
Three cubes with edges measuring 5 inches are stacked on top of one another.
What is the total volume of the 3 cubes?
Answer:
The total volume of the 3 cubes is 375 in³,

Explanation:
Given three cubes with edges measuring 5 inches are stacked on top of one another.
3 X (5 inches X 5 inches X 5 inches) = 3 X (125 in³) = 375 in³.

Question 24.
The rectangular container shown contains 2 liters of water.
How much more water must be added to fill the container completely?
Give your answer in liters.

Answer:
1,750 cubic cm more water must be added to fill the container completely,

Explanation:
Given rectangular cuboid volume is 10 cm X 25 cm X 15 cm = 3,750 cubic cms as
the rectangular container shown contains 2 liters of water.
Equal to 2 X 1000 = 2,000 cubic cms  so much more water must be
added to fill the container completely is 3,750 cubic cm – 2,000  cubic cm = 1,750 cubic cm.

Solve. Show your work.

Question 25.
A container is 28 centimeters long, 1 4 centimeters wide, and 10 centimeters high.
It is half-filled with juice. Kathy pours 500 milliliters of water into the
container to make a juice drink. Find the volume of juice drink in the container now.
Give your answer in liters and milliliters.
Answer:
Given a container is 28 centimeters long, 1 4 centimeters wide, and 10 centimeters high.
Volume of container is 28 cm X 14 cm X 10 cm = 3,920 cubic centimeters,
It is half-filled with juice. \(\frac{1}{2}\) X 3,920 = 1,960 cubic centimeters or
1,960 milliliters now Kathy pours 500 milliliters of water into the container
to make a juice drink. Therefore the volume of juice drink in the container now is
1,960 milliliters + 500 milliliters = 2,460 milliliters and 1,000 milliliters = 1 liter,
So 2 L 460 milliliters.

Question 26.
The fish tank shown is filled with 4 liters of water per minute from a faucet.
How long does it take to fill the tank completely?

Answer:
Long does it will take to fill the tank completely is 6 minutes,

Explanation:
Given the tank has length is 45 cm, width is 16 cm and height is 30 cm,
volume = 45 cm X 16 cm X 30 cm = 2,16,00 cubic cms 21 liters 600 milliliters,
as fish tank shown is filled with 4 liters of water per minute from a faucet,
Long does it will take to fill the tank completely is 21,600 ÷ 4 = 5 minutes 400 ≈ 6 minutes.

Solve. Show your work.

Question 27.
A tank with a square base with edges measuring 20 centimeters and a
height of 36 centimeters is \(\frac{2}{3}\)-filled with water.
Each minute, 2 liters of water leak out of the tank through a crack in the bottom.
How long does it take for all the water to leak out?

Answer:
It will be approximately 5 minutes long for water to leak out,

Explanation:
Given a tank with a square base with edges measuring 20 centimeters
and a height of 36 centimeters, So volume is
20 cm X 20 cm X 36 cm = 14,400 cubic centimeters ,
and tank is filled with \(\frac{2}{3}\)-filled with water means
\(\frac{2}{3}\) X 14,400 = 9,600 milliliters and each minute 2 liters of
water leak out of the tank through a crack in the bottom is
9,600 ÷ 2,000 = 4.8 ≈ 5minutes.

Read More:

Bse Smallcap Index

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 16 Practice 3 Addition of Time provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 16 Practice 3 Answer Key Addition of Time

Add

Example

Question 1.

So, 3 h 25 min + 5 h 30 min
= ______ h _______ min.

______ h + ______ h = ______ h
______ min + ______ min = ______ min
______ h + ______ min = ______ h ______ min
Answer: 8 hour 55 minutes.
Follow the below steps :
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 3 hours+5 hours
=8 hours.
Step 2: Add minutes.
= 25 min+30 min
= 55 min.
Finally, we get in hours and minutes are 8 hours 55 minutes.

Question 2.

So, 7 h 30 min + 3 h 14 min
= ______ h _______ min.

______ h + ______ h = ______ h
______ min + ______ min = ______ min
______ h + ______ min = ______ h ______ min
Answer: 10 hours 44 minutes.
Follow the below steps :
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 7 hours+3 hours
=10 hours.
Step 2: Add minutes.
= 30 min+14 min
= 44 min.
Finally, we get in hours and minutes are 10 hours 44 minutes.

Question 3.

So, 2 h 50 min + 1 h 9 min
= ______ h _______ min.

______ h + ______ h = ______ h
______ min + ______ min = ______ min
______ h + ______ min = ______ h ______ min
Answer: 3 hour 59 minutes.
Follow the below steps :
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 2 hours+1 hours
=3 hours.
Step 2: Add minutes.
= 50 min+9 min
= 59 min.
Finally, we get in hours and minutes are 3 hours 59 minutes.

Add

Question 4.
20 min + 55 min = __________ min

Answer: 1 hour 15 minutes.
Explanation:

The given question is 20 min+55 min=X min.
If we add 20 min and 55 min then we get 20+55=75 min.
To this 75 minutes, we need to convert in hours and minutes.
75 can be written as 60 and 15:
1 hour=60 minute.
And remaining 15 minutes will stay the same.
Finally, 75 min=1 hours 15 minutes.

Question 5.
55 min + 45 min = __________ min

Answer:

The given question is 55 min+45 min=X min.
If we add 55 min and 45 min then we get 55+45=100 min.
To this 100 minutes, we need to convert in hours and minutes.
100 can be written as 60 and 40:
1 hour=60 minute.
And remaining 40 minutes will stay the same.
Finally, 100 min=1 hours 40 minutes.

Question 6.
4 h 46 min + 2 h 14 min = _____ h _____ min
= ________ h
Answer: 7 hours.
Follow the below steps :
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 4 hours+2 hours
=6 hours.
Step 2: Add minutes.
= 46 min+14 min
= 60 min.
Step 3: Apply rule 3. We got 60 minutes. So subtract 60 and add 1 to the hours.
=60-60
=0.
Adding 1 to the hours:
= 6 hours+1
=7 hours.
Therefore,  the answer is 7 hours.

Question 7.
1 h 48 min + 3 h 35 min = _____ h _____ min
= _____ h _____ min
Answer: 5 hours 23 minutes.
Follow the below steps :
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 1 hours+3 hour
=4 hours.
Step 2: Add minutes.
= 48 min+35 min
= 83 min.
Step 3: Apply rule 3. We got 60 minutes. So subtract 60 and add 1 to the hours.
=83-60
=23.
Adding 1 to the hours:
= 4 hours+1
=5 hours.
Therefore,  the answer is 5 hours 23 minutes.

Solve.

Question 8.
Grace spends 50 minutes practicing the piano. Then she spends 2 hours 1 5 minutes doing her homework. How long does she spend on the two tasks?
Answer:
The minutes she spends on the piano=50 min
The time spends on her homework=2 h 15 min
The total time she spends on both works=X
By following some steps we need to calculate the total hours and min.
1. Add the hours
2. Add the minutes
3. If the minutes are 60 or more, subtract 60 from the minutes and add 1 to hours
Explanation:
Step 1: First add hours.
= 0+2
=2 hours.
Step 2: Add minutes.
= 50 min+15 min
= 65 min.
Step 3: Apply rule 3. We got 60 minutes. So subtract 60 and add 1 to the hours.
=65-60
=5.
Adding 1 to the hours:
= 2 hours+1
=3 hours.
Therefore,  the answer is 3 hours 5 minutes.

Read More:

Abb Calculator

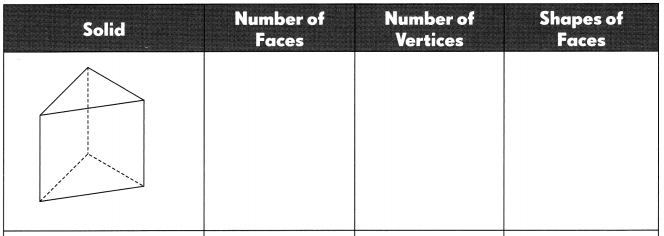
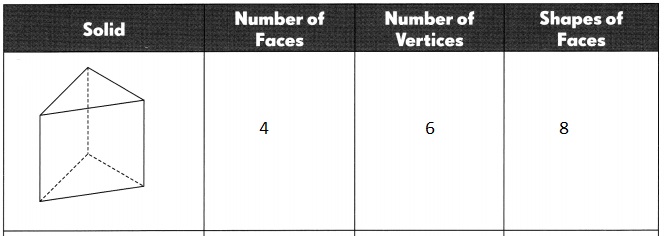
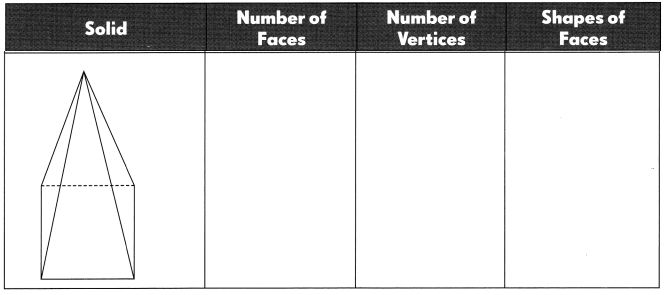
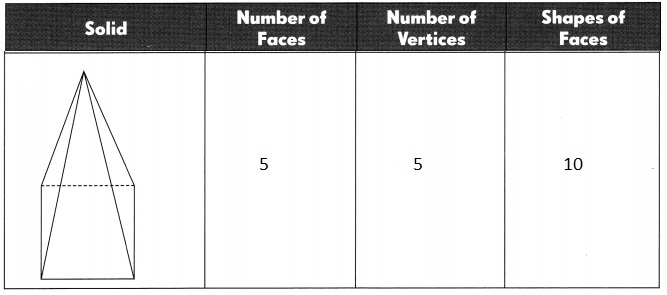
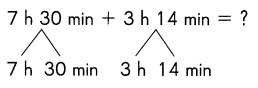
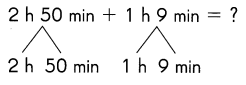
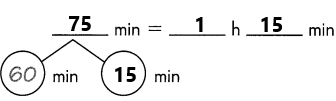
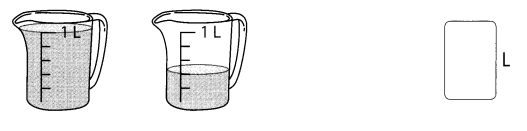
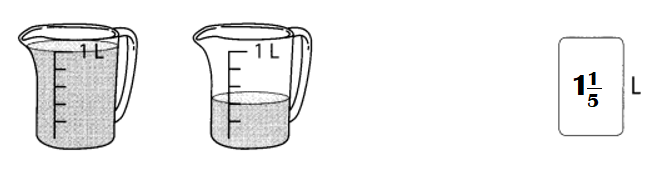
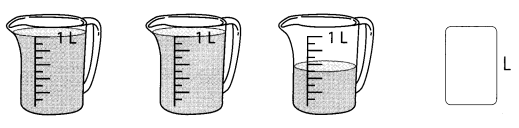
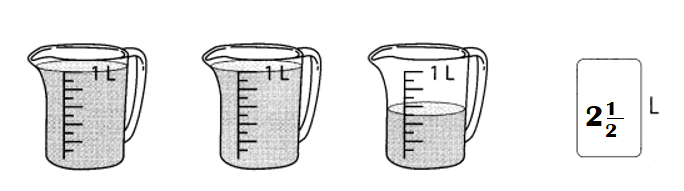
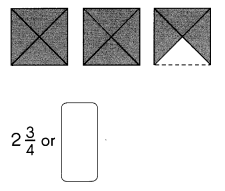
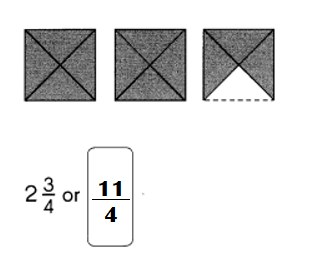
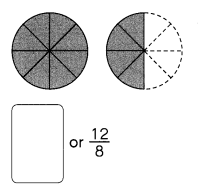
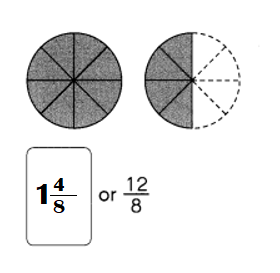
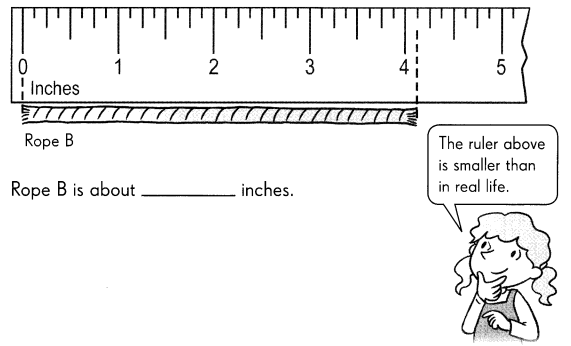
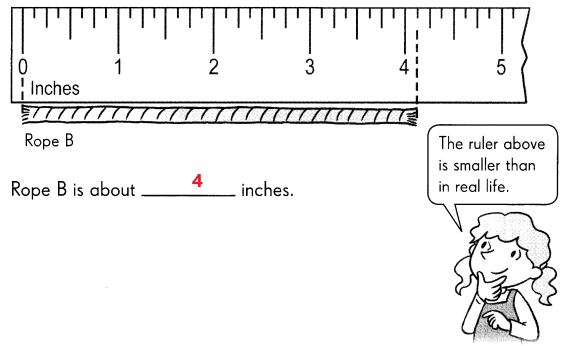
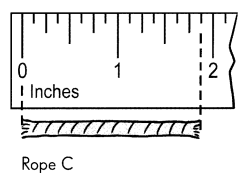
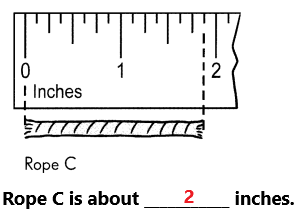
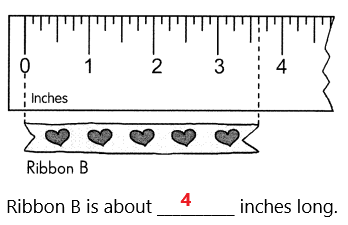
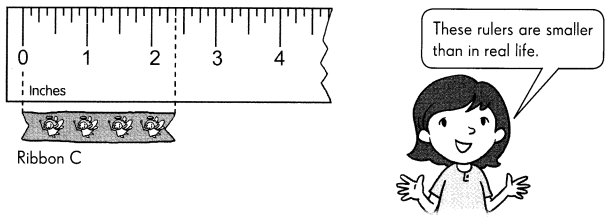
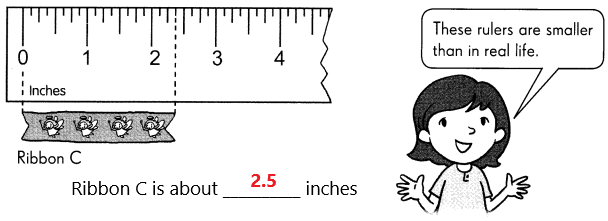
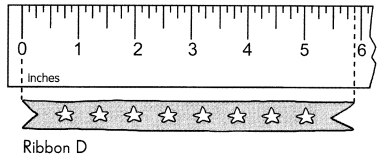
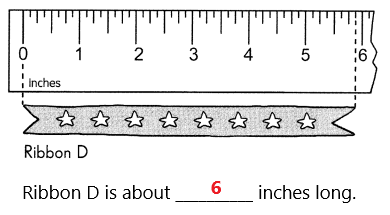
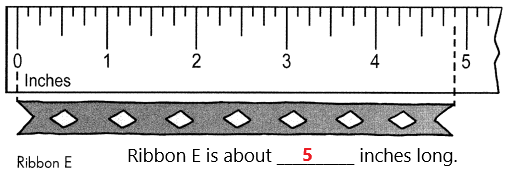
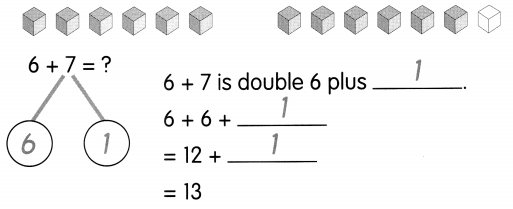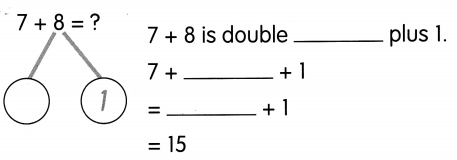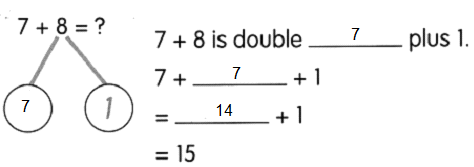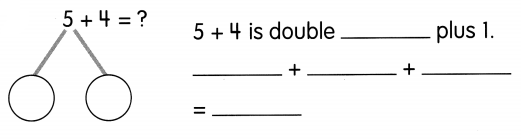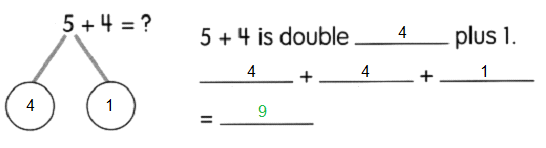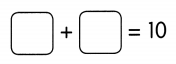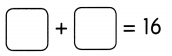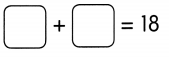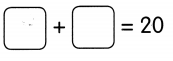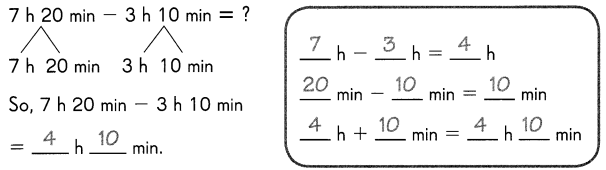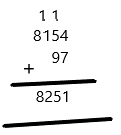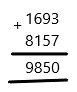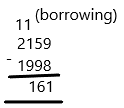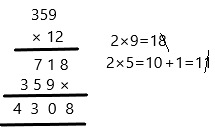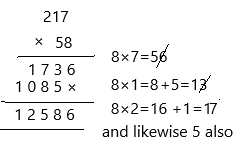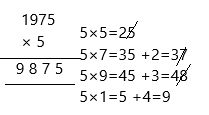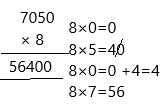Go through the Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 1 and 2 to finish your assignments.

Math in Focus Grade 5 Cumulative Review Chapters 1 and 2 Answer Key

Concepts and Skills

Write each number in standard form. (Lesson 1.1)

Question 1.
One hundred thousand, seventy _____
Answer:
100,070,

Explanation:
Standard form or expanded notation is a way of writing numbers to see the math value of individual digits.
Numbers are separated into individual place values to write in numbers.
One hundred thousand = 100 x 1000,
Seventy = 7 x 10,
Add both 100,000 + 70 = 100,070.

Question 2.
Five hundred sixty thousand _____
Answer:
560,000,

Explanation:
Standard form or expanded notation is a way of writing numbers to see the
math value of individual digits.
Numbers are separated into individual place values to write in numbers.
Five hundred sixty thousand = 560 x 1000 = 560,0 00.

Question 3.
Five million, eighty thousand, five _____
Answer:
50,080,005,

Explanation:
Standard form or expanded notation is a way of writing numbers to see the
math value of individual digits.
Numbers are separated into individual place values to write in numbers.
Five million = 5 x 1,000,000,
Eighty thousand = 80 x 1000,
Five = 5,
Add all the numbers = 50,080,005.

Question 4.
Two million, four hundred thousand, seven hundred twenty ___
Answer:
2,400,720,

Explanation:
Standard form or expanded notation is a way of writing numbers to see the
math value of individual digits.
Numbers are separated into individual place values to write in numbers.
Two million = 2 x 1,000,000,
Four hundred thousand = 400 x 1000,
Seven hundred twenty = 720,
Add all numbers = 2,400,720.

Write each number in word form. (Lesson 1.1)

Question 5.
120, 450 _____
Answer:
One hundred twenty thousand four hundred fifty,

Explanation:
Word form  and stand forms are both are reciprocal to each other.
Numbers are separated into individual place values to write in word form.

Question 6.
500, 312 _______
Answer:
Five hundred thousand three hundred twelve,

Explanation:
Word form  and stand forms are both are reciprocal to each other.
Numbers are separated into individual place values to write in word form.

Question 7.
1,050,400 _____
Answer:
One million fifty thousand four hundred,

Explanation:
Word form  and stand forms are both are reciprocal to each other.
Numbers are separated into individual place values to write in word form.

Question 8.
5,732,800 _____
Answer:
Five million seven hundred thirty-two thousand eight hundred,

Explanation:
Word form  and stand forms are both are reciprocal to each other.
Numbers are separated into individual place values to write in word form.

Complete. (Lesson 1.2)

In 1,238,906:
One million two hundred thirty-eight thousand nine hundred six

Question 9.
the digit 8 stands for _____
Answer:
8 stands for eight thousand,

Explanation:
Count the place values from right hand side at first,
So, 8 stands in thousand’s place.

Question 10.
the digit 9 stands for _____
Answer:
9 stands for nine hundred,

Explanation:
Count the place values from right hand side at first,
So, 9 stands in hundred’s place.

Question 11.
the digit 1 stands for _____
Answer:
1 stands for one million,

Explanation:
Count the place values from right hand side at first,
So, 1 stands in million’s place.

State the value of the digit 3 in each number. (Lesson 1.2)

Question 12.
538,426: ____
Answer:
The value of the digit 3 is thirty thousand,

Explanation:
Count the place values from right hand side at first,
So, 3 stands in thousand’s place.

Question 13.
1,325,407: ____
Answer:
The value of the digit 3 is three hundred thousands,

Explanation:
Count the place values from right hand side at first.
So, 3 stands in 300 thousand’s place.

Complete. (Lesson 1.2)

Question 14.
In 807,456, the digit ____ is in the thousands place.
Answer:
7 is in the thousands place,

Explanation:
Count the place values from right hand side to the know the place value of 7,
So, 7 is in thousand’s place.

Question 15.
In 5,486,302, the digit ___ is in the millions place.
Answer:
5 is in the millions place,

Explanation:
Count the place values from right hand side to know the place value of 5,
So, 5 is in millions place.

Question 16.
In 305,128, the digit 0 is in the ____ place.
Answer:
0 is in the ten thousand place,

Explanation:
Count the place values from right hand side to know the place value of 0,
So, 0 is in ten thousand’s place.

Question 17.
In 7,614,892, the digit 6 is in the ____ place.
Answer:
6 is in the hundred thousand’s place,

Explanation:
Count the place values from right hand side to know the place value of 6,
So, 6 is in hundred thousand’s place.

Question 18
918,230 = ___ + 10,000 + 8,000 + 200 + 30
Answer:
9,00,000,

Explanation:
Count the place values from right hand side to know the place value of 9.
So, 9 is in millions’ place.
918,230 = 900,000 + 10,000 + 8,000 + 200 + 30.

Question 19.
538,417 = 500,000 + ____ + 8,000 + 400 + 10 + 7
Answer:
30,000,

Explanation:
Count the place values from right hand side to know the place value of 9.
So, 3 is in ten thousand’s place.
538,417 = 500,000 + 30000 + 8,000 + 400 + 10 + 7.

Question 20.
6,000,000 + 30,000 + 90 = _____
Answer:
9,030,090,

Explanation:
Standard form or expanded notation is a way of writing numbers to see the
math value of individual digits,
6,000,000 + 30,000 + 90 =9,030,090.

Fill each 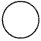with >or <‘. (Lesson 1.3)

Question 21.
185,263 183,256
Answer:
185,263 > 183,256,

Explanation:
First compare both the numbers,
by subtracting the smaller number 183,256 from bigger number 185,263,
then put the appropriate symbol in the circle.

Question 22.
5,060,345 995,863
Answer:
5,060,345 > 995,863,

Explanation:
Count the place values of both the numbers.
in 5,060,345 place values are more.
So, put the greater than symbol in the circle.

Question 23.
899,506 900,650
Answer:
899,506 < 900,650,

Explanation:
First compare both the numbers,
by subtracting the smaller number 899,506 from bigger number 900,650
then put the appropriate symbol in the circle.

Question 24.
231623 231,621
Answer:
231,623 > 231,621,

Explanation:
First compare both the numbers,
by subtracting the smaller number 231,621 from bigger number 231,621
then put the appropriate symbol in the circle.

Order the number from greatest to least. (Lesson 1.3)

Question 5.

Answer:
1,280,500    528,100    5280,100   528,010,

Explanation:
Arranging the numbers from greatest to smallest is known as descending order.

Find the rule. Then complete the number pattern. (Lesson 1.3)

Question 26.

Rule: ________
Answer:
276,300   286,300    296,300    306,300    316,300,

Rule:
Addition of 1000,
n + 1000,

Explanation:
Number patterns are the patterns in which a list of numbers follows a certain sequence.
Generally, the patterns establish the relationship between two numbers.
It is also known as the sequences of series in numbers.

Estimate by rounding. (Lesson 1.4)

Question 27.
7,512 + 3,281 _______
Answer:
10,800,

Explanation:
Estimate of 7,512 is 7,500,
Estimate of 3,281 is 3,300,
7,500 + 3,300 = 10,800.

Question 28.
6,528 – 5,938 _______
Answer:
500,

Explanation:
Estimate of 6,528 is 6500,
Estimate of 5,938 is 6000,
6,500 – 6,000  = 500.

Question 29.
1,592 × 5 _____
Answer:
80,000,

Explanation:
Estimate of 1,592 is 1600,
1,600 x 5 = 8,000.

Question 30.
2,576 ÷ 3 _______
Answer:
866,

Explanation:
Estimate of 2,576 is 2,600,
2,600 ÷ 3 =  866.

Estimate using front-end estimation with adjustment. (Lesson 1.4)

Question 31.
4,087 + 3,910 + 9,125
Answer:
17,000,

Explanation:
Estimate of 4,087 is 4,000,
Estimate of 3,910 is 4,000,
Estimate of 9,125 is 9,000,
4,000 + 3,000 + 9,000 = 16,000,
000 + 900 + 100 = 1,000,
16,000 + 1,000 = 17,000.

Estimate using front-end estimation with adjustment. (Lesson 1.4)

Question 32.
8,685 + 6,319 + 7,752
Answer:
22,700,

Explanation:
Estimate of 8,685 is 8,000,
Estimate of 6,319 is 6,000,
Estimate of 7,752 is 7,000,
8,000 + 6,000 + 7,000 = 21,000,
600 + 300 + 800 = 1,700,
21,000 + 1,700 = 22,700.

Question 33.
5,879 – 1,143
Answer:
4,800,

Explanation:
Estimate of 5,879 is 5,000,
Estimate of 1,143 is 1,000,
5,000 – 1,000 = 4,000,
900 – 100 = 800,
4,000 + 800 = 4,800.

Question 34.
7,974 – 2,660
Answer:
5,200,

Explanation:
Estimate of 7,974 is 7,000,
Estimate of 2,660 is 2,000,
7,000 – 2,000 = 5,000,
900 – 700 = 200,
5,000 + 200 = 5,200.

Complete. Remember to write the correct units in your answers.
You may use your calculator where necessary. (Lesson 2.1)

Question 35.
Find the area of a square that has sides of length 96 inches.
________
Answer:
9,216 square inches,

Explanation:
Area of a square = side x side,
Area = 96 x 96 square inches,
Area = 9,216 square inches.

Question 36.
Ms. Suarez has $5,651. Mr. Knox, has $853 more than Ms. Suarez. How much does Mr. Knox have?
___________
Answer:
$6504,

Explanation:
Ms. Suarez has $5,651,
Mr. Knox has $5,651 + $853 = $6504,
Mr. Knox have $6504.

Complete. Remember to write the correct units in your answers.

You may use your calculator where necessary. (Lesson 2.1)

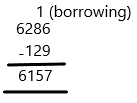
Question 37.
There are 176 gallons of gas in Tank A. There are 19 gallons less gas in Tank B.
How many gallons of gas are there in Tank B?
__157 gallons of gas______
Answer:
157 gallons of gas,

Explanation:
Tank A    176 gallons of gas,
Tank B    176 – 19 = 157 gallons of gas.

Question 38.
A truck is loaded with 25 similar crates. The total weight of the crates is 2,000 pounds.
What is the weight of each crate?
___80 pounds______
Answer:
80 pounds,

Explanation:
A truck is loaded with 25 similar crates,
The total weight of the crates is 2,000 pounds,
The weight of each crate 2,000 ÷ 25 = 80 pounds.

Multiply. (Lesson 2.2)

Question 39.
315 × 10 = __3,150_____
Answer:
3,150,

Explanation:
315 x 10 = 300 x 10 + 10 x 10 + 5 x 10,
= 3000 + 100 + 50,
= 3,150.

Question 40.
25 × 100 = _2,500___
Answer:
2,500,

Explanation:
100 x 25 = 20 x 100 + 5 x 100,
= 2000 + 500,
= 2,500.

Question 41.
238 × 1,000 = __238,000__
Answer:
238,000,

Explanation:
238 x 1000 = 200 x 1000 + 30 x 1000 + 8 x 1000,
= 2,00,000 + 30,000 + 8,000,
= 238,000.

Question 42.
147 × 50 = _7,350___
Answer:
7,350,

Explanation:
147 x 50 = 100 x 50 + 40 x 50 + 7 x 50,
= 5,000 + 2,000 + 350,
= 7,350.

Question 43.
63 × 200 = _12,600___
Answer:
12,600,

Explanation:
60 x 200 + 3 x 200 = 12000 + 600,
= 12,600.

Question 44.
906 × 7,000 = __6,342,000__
Answer:
6,342,000,

Explanation:
906 x 7,000 = 900 x 7,000 + 0 x 6,000 + 6 x 7,000,
=6,300,000 + 0 + 42,000
= 6,342,000.

Estimate by rounding. (Lesson 2.2)

Question 45.
41 × 58 ______
Answer:
2,400,

Explanation:
41 x 58 = 40 x 60,
= 2,400.

Question 46.
297 × 32 _____
Answer:
9,000,

Explanation:
300 x 30 = 9,000.

Question 47.
1,087 × 21= __22,000___
Answer:
22,000,

Explanation:
1,100 x 20 = 22,000.

Question 48.
4.975 × 78 = __388.05___
Answer:
388.05,
Estimate: 400,

Explanation:
4.975 X 78 =388.05,
Estimate of 4.975 is 5,
Estimate of 78 is 80,
So, 5 x 80 = 400.

Multiply. (Lesson 2.3)

Question 49.
19 × 10² = ____
Answer:
1,900,

Explanation:
19 x 10²,
10² = 10 x 10 = 100,
= 19 x 100,
= 1,900.

Question 50.
186 × 10² = __18,600__
Answer:
18,600,

Explanation:
186 x 10² = 10² = 10 x 10 = 100,
= 186 x 100,
= 100 x 100 + 80 x 100 + 6 x 100,
= 10,000 + 8,000 + 600,
= 18,600.

Question 51.
65 × 10³ = __65,000__
Answer:
65,000,

Explanation:
65 x 10³,
10³ = 10 x 10 x 10 = 1,000,
= 65 x 1,000,
= 65,000.

Question 52.
154 × 10³ = _1,54,000__
Answer:
1,54,000,

Explanation:
154 x 10³ = 10³ = 10 x 10 x 10 = 1,000,
=154 x 1,000,
= 1,54,000.

Multiply. Estimate to check if your answers are reasonable. (Lesson 2.4)

Question 53.
82 × 45 = ____
Answer:
3,600,

Explanation:
Estimate of 82 is 80, 80 x 45 = 80 x 40 + 80 x 5,
= 3,200 + 400,
= 3,600,

Check
82 x 45,
Multiply 82 by 5,
Multiply 82 by 4 tens,
410 + 3,280 = 3,690,
Hence, Answer is reasonable.

Question 54.
78 × 21 = __1,600___
Answer:
1,600,

Explanation:
Given 78 X 21 we
Estimate of 78 is 80,80 x 20 = 1,600,
Check
78 x 21,
Multiply 78 by 20,
Multiply 78 by 1 ten,
1,560 + 78 = 1,638,
Hence, Answer is reasonable.

Question 55.
275 × 59 = __16,500__
Answer:
16,500,

Explanation:
275 x 60 = 200 x 60 + 70 x 60 + 5 x 60,
= 12000 + 4200 + 300,
= 16,500
Check
275 x 59 = 16,225.
Hence, Answer is reasonable.

Question 56.
738 × 96 = _74,000___
Answer:
74,000,

Explanation:
= 740 x 100 = 700 x 100 + 40 x 100 + 0 x 100,
= 70,000 + 4,000 + 0,
= 74,000,
Check
738 x 96 = 70,848,
Hence, Answer is reasonable.

Multiply. Estimate to check if your answers are reasonable. (Lesson 2.4)

Question 57.
4,672 × 73 = _327,040___
Answer:
4,672 x 73,
4,672 x 70 = 327,040,
4,672 x 3 = 14,016,
327,040+14,016 = 341,056,
Check
4,700 x 70 = 3,29,000,
Hence, Answer is reasonable.

Question 58.
8,781 × 26 = _175,620___
Answer:
8,672, x 20 = 175,620,
8,781 x 6 = 52,686,
175,620 + 52,686 = 2,28,306,
8,800 x 25 = 2,20,000.
Hence, Answer is reasonable.

Divide. (Lesson 2.5)

Question 59.
3,560 ÷ 10 = _356__
Answer:
356,

Explanation:
3,560 ÷ 10,
3,560 is dividend and 10 is divisor
Count the number of zeros in dividend and divisor and
just move the decimal point one point to the left side.

Question 60.
1,900 ÷ 100 = _19___
Answer:
19,

Explanation:
1,900 ÷ 100,
1,900 is dividend and 10 is divisor
Count the number of zeros in dividend and divisor and
just move the decimal point two points to the left side.

Question 61.
17,000 ÷ 1,000 = __17__
Answer:
17,

Explanation:
17,000 ÷ 1,000,
17,000 is dividend and 1,000 is divisor
Count the number of zeros in dividend and divisor and
just move the decimal point 3 points to the left side.

Question 62.
900 ÷ 60 = __15__
Answer:
15,

Explanation:
900 ÷ 60 = (900 ÷ 10) ÷ 6,
= 90 ÷ 6 =  15.

Question 63.
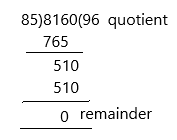
96,000 ÷ 400 = __240__
Answer:
240,

Explanation:
96,00 ÷ 400 = (96,000 ÷ 100) ÷ 4,
= 9,60 ÷ 4,
=  240.

Question 64.
504,000 ÷ 9,000 = _56__
Answer:
56,

Explanation:
504,000 ÷ 9,000 = (504,000 ÷ 1000) ÷ 9,
= 504 ÷ 9,
=  56.

Estimate. (Lesson 2.5)

Question 65.
4,593 ÷ 53 = __90__
Answer:
90,

Explanation:
Estimate of 4,593 is 4,500,
Estimate of 53 is 50,
So, 4500 ÷ 50 = 90,
50 x 90 = 4,500.

Question 66.
6,298 ÷ 164 = __30__
Answer:
30,

Explanation:
Estimate of 6,298 is 6,000,
Estimate of 164 is 200,
So, 6,000 ÷ 200 = 30,
200 x 30 = 6,000.

Question 67.
7,623 ÷ 4,451 = __2__
Answer:
2,

Explanation:
Estimate of 7,623 is 8,000,
Estimate of 4,451 is 4,000,
So, 8,000 ÷ 4,000 = 2,
4,000 x 2 = 8,000.

Question 68.
4,239 ÷ 73 = _60___
Answer:
60,

Explanation:
Estimate of 4,239 is 4,200,
Estimate of 73 is 70,
So, 4200 ÷ 70 = 60,
70 x 60 = 4,200,

Divide. (Lesson 2.6)

Question 69.
96 ÷ 16 = _6__
Answer:
6,

Explanation:
96 ÷ 16,
16 rounds to 10.
6 × 10 = 60,
The quotient is about 6.
6 × 16 = 96,

Question 70.
57 ÷ 23 = __2 R 11__
Answer:
2 R 11,

Explanation:
57 ÷ 23,
23 rounds to 20.
3 × 20 = 60,
The quotient is about 3.
3 × 23 = 69,
The estimated quotient is too big. Try 2.

Question 71.
459 ÷ 27 = _17___
Answer:
17,

Explanation:
459 ÷ 27,
459 rounds to 500.
27 rounds to 30,
500 ÷ 30 = 16.6,
The quotient is about 17.

Question 72.
503 ÷ 15 = _33 R 8___
Answer:
33 R 8,

Explanation:
503 ÷ 15,
503 rounds to 500.
15 rounds to 20,
20 x 25 = 500,
The quotient is about 33 and remainder is 8.

Simplify. (Lesson 2.7)

Question 73.
60 + 12 – 36 = _36__
Answer:
36,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 60 + 12 = 72,
Step 2: 72 – 36 = 36.

Question 74.
10 × 9 ÷ 3 = __30__
Answer:
30,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 9 ÷ 3 = 3,
Step 2: 10 x 3 = 30.

Question 75.
29 + 42 ÷ 6 = _36__
Answer:
36,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 42 ÷ 6 = 7,
Step 2: 29 + 7 = 36.

Question 76.
(90 – 85) × 7 = _35__
Answer:
35,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1 : 90 – 85 = 5,
Step 2: 5 x 7 = 35.

Question 77.
50 × 8 + 12 ÷ 4 = _403___
Answer:
403,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 12 ÷ 4 = 3,
Step 2: 50 x 8 = 400,
Step 3: 400 + 3 = 403.

Question 78.
69 ÷ 3 – 3 + 10 = _30__
Answer:
30,

Explanation:
The order of operation in math is a set of rules revolving around 4 major operators.
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply DMAS rule.
DMAS is the elementary rule for the order of operation of the Binary operations.
This States that Division will be done before Multiplication,
multiplication before addition and addition before subtraction.
Step 1: 69 ÷ 3 = 23
Step 2: 23 – 3 = 20
Step 3: 20 + 10 = 30.

Evaluate. (Lesson 2.7)

Question 79.
56 + {12 – [18 – (3 + 9)]} = _62___
Answer:
62,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 3 + 9 = 12,
Step 2: 18 – 12 = 6,
Step 3: 12 – 6 = 6,
Step 4: 56 + 6 = 62.

Question 80.
100 ÷ (20 + 5) + [(18 – 3) × 4] = __64__
Answer:
64,

Explanation:
According to the order of operations, there is a particular sequence which we need to follow,
on each operator while solving the given mathematical expression we apply BODMAS rule.
BODMAS is the elementary rule for the order of operation of the Binary operations.
The acronym stands for B – Brackets, O – Order of powers, D – Division,
M – Multiplication, A – Addition, and S – Subtraction.
Step 1: 20 + 5 = 25,
Step 2: 100 ÷ 25 = 4,
Step 3: 18 – 3 = 15,
Step 4: 15 x 4 = 60,
Step 5:  60 + 4 = 64.

Problem Solving

Solve. Show your work.

Question 81.
Tony had an equal number of cranberry bars and walnut bars. He gave away 66 cranberry bars.
He then had 4 times as many walnut bars as cranberry bars left. How many bars did he have at first?
Answer:
176 bars at first,

Explanation:
Cranberry ‘c’ = ‘w’ Walnut bars,
4(c – 66) = w,
4c – 264=w,
4c – 264=c,
3c – 264=0(Zero),
3c = 264,
c = 88 cranberry bars,
w = 88 walnut bars,
88 + 88=176 bars at first,
check:
88 – 66 = 22 and 88 is 4 times 22.

Solve. Show your work.

Question 82.
Mrs. Turner had 20 yards of fabric at first. She made 5 similar curtains.
She used 3 yards of fabric for making each curtain. Then she used another 2 yards of fabric to
make a cushion cover. How much fabric does she have left?
Answer:
3 yards,

Explanation:
Total fabric = 20 yards,
used to make curtains = 5 x 3 = 15,
used to make cushion cover = 2,
leftover = 20 – (15 + 2) = 20 – 17 = 3 yards.

Question 83.
At a school fair, a fifth-grade class sold 25 liters of orange juice.
The orange juice was sold in cups containing 200 milliliters and 300 milliliters.
An equal number of cups containing 200 milliliters and 300 milliliters were sold.
How many cups of orange juice did the class sell?
Answer:
100 cups,

Explanation:
25L of orange juice = 25,000 ml,
200 + 300=500 ml,
25000 ml ÷  500 ml = 50 cups,
2 x 50 cups = 100 cups.

Solve. Show your work.

Question 84.
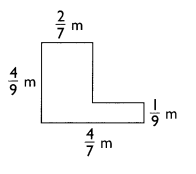
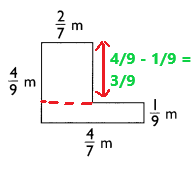
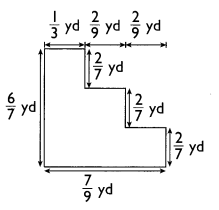
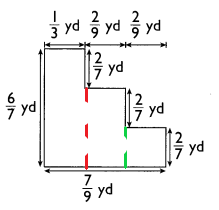
Mikhail used 220 inches of wire to make this figure.

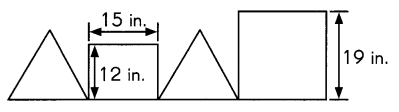
The figure is made up of two identical triangles, a 15-inch by 12-inch rectangle and
a square of side 1 9 inches. What is the length of one side of each triangle if all the sides
of the triangles are equal in length?
Answer:
15 inch is the length of one side of each triangle,

Explanation:
Rectangle = 15 + 12 + 15 +12 = 54 inches,
Square = 19 x 4 = 76 inches,
220 – ( 54 + 76) = 90 inches,
2 triangles = 6 sides = 90 ÷ 6 = 15 inch is the length of one side of each triangle.

Question 85.
A shop owner bought 260 handbags at 5 for $25. She then sold all of them at 2 for $1 8.
How much money did she make?
Answer:
$1,040,

Explanation:
A shop owner bought 260 handbags at 5 for $25,
260 ÷ 5 = 52,
52 x 25 = 1300,
she bought the hand bag for $1300,
She then sold all of them at 2 for $18.
260 ÷ 2 = 130,
130 x 18 = $2,340,
She sold them for $2,340,
Total money she makes
$2,340 – $1,300 = $1,040.

Solve. Show your work.

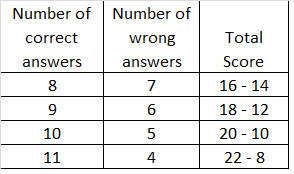
Question 86.
Alan scored a total of 14 points for answering all 15 questions on a math quiz.
For every correctly answered question, Alan got 2 points. For every wrong answer,
he lost 2 points. How many questions did he answer correctly?
Answer:
He answered 11 questions correctly,

Explanation:
For every correctly answered question, Alan got 2 points.
For every wrong answer, he lost 2 points.

Question 87.
Beth and Lewis buy the same amount of fish flakes. If Beth feeds her goldfish 14 fish flakes each day,
a container of flakes will last 20 days. If Lewis feeds his goldfish 8 fish flakes each day,
how many more days will the container of flakes last for Lewis?
Answer:
The container will last 15 more days,

Explanation:
Beth feeds her goldfish 14 fish flakes each day, a container of flakes will last 20 days.
14 x 20 = 280,
If Lewis feeds his goldfish 8 fish flakes each day.
280 ÷ 8 = 35,
35 days – 20 days = 15 days,
The container will last 15 more days.

Solve. Show your work.

Question 88.
Joan can pick 9 pounds of strawberries in one hour.

a. How long does she take to pick 72 pounds of strawberries?
Answer:
8 hours,

Explanation:
72 pounds ÷ 9 pounds = 8,
Joan takes 8 hours to pick 72 pounds.

b. Joan is paid $12 per hour. How much does Joan earn if she picks twice the
total weight of strawberries in a.?
Answer:
Joan earn $192,

Explanation:
8 hrs x 2 = 16 hrs,
16 x $12 = $192,
Joan earn $192.

Question 89.
There are 2,488 students in Washington School. There are 160 more students in Kent School.
The number of students in Bellow School is half the total number of students in
Washington School and Kent School. How many students are there in Bellow School?
Answer:
There are 2,568 students in the Bellow school,

Explanation:
There are 2,488 students in Washington School.
There are 160 more students in Kent School.
2,488+ 160 = 2,648 students,
The number of students in Bellow School is half the total number of students in
Washington School and Kent School.
2,488 students + 2,648 students = 5,136 students,
Total students in Bellow School
5,136 students ÷ 2 = 2,568 students.

Solve. Show your work.

Question 90.
Jasmine mixes 1,250 milliliters of syrup with twice as much water to make lemonade.
She then pours the lemonade equally into 15 glasses.
How much lemonade does each glass contain? Give your answer in milliliters.
Answer:
Each glass has 250 ml of lemonade,

Explanation:
Jasmine mixes 1,250 milliliters of syrup with twice as much water to make lemonade,
1,250 x 2 = 2,500ml of water 1,250 + 2500= 3,750 ml,
She then pours the lemonade equally into 15 glasses.
3,750 ml ÷ 15 = 250 ml.

Must Try:

Straddle Calculator

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 16 Practice 5 Elapsed Time provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 16 Practice 5 Answer Key Elapsed Time

Tell what time it will be.

Question 1.
2 hours after 8:00 P.M. _____________
Answer: 10:00 P.M
Explanation:
By using a timeline we can calculate elapsed time:
2 hours after 8:00 PM means if we add 8 and 2 then we get 8+2=10 hours.

1. The start time and end times are labelled on an end of a timeline.
2. Between 8:00 and 10:00 are the hours of 9:00, which are marked on the timeline.
3. Between 8:00 and 10:00 there are 2 hours.

Question 2.
3 hours before 6:40 A.M. ______________
Answer: 3:40 hours
Explanation:
1. Calculating the elapsed time means finding the difference between two times.
2. To calculate the elapsed time, it is easiest to count up in hours.
3. Here asked 3 hours before the given time. So we need to subtract 6:40 And 3 hours then we get 6:40-3:00=3:40.
4. The elapsed time is 3 hours 40 minutes A.M.

Question 3.
30 minutes after 1:36 P.M. _______________
Answer: 2:01 P.M
Explanation:

1. The start time and end times are labelled on an end of a timeline.
2. Between 1:36 and 2:01 are the hours of 2:00, which are marked on the timeline.
3. We subtract the 36 minutes of 1:36 from the 60 minutes to get 24 minutes. There are 24 minutes from 1:36 pm and 2:00 pm.
4. Between 1:36 pm and 1:40 there are 4 minutes.
5. Between 1:40 pm and 2:00 pm there are 25 minutes.
6. We need to calculate for 30 minutes. And from 2:00 pm to 2:01 pm, there is 1 minute.
7. Now adding all the minutes, 4 +25+1=30.
8. Finally, 1:36 pm after 30 minutes are 2:01 pm.

Question 4.
45 minutes before 7:05 A.M. _____________
Answer:
Here given end time that is 7:05 AM. We need to calculate the start time.

Explanation:
1. Now I calculated the start time by using the given 45 minutes.
2. First I wrote 7:05 AM on the timeline as an end date. From there I started counting start times.
3. Then I take the earliest time to 7:05 AM that is 7:00 AM. Between both timings, there are 5 minutes.
4. And then I take 6:30 AM which is nearer to 7:00 AM. Between both timings, there are 30 minutes.
5. And we need to calculate for extra 10 minutes. From 6:30 to 6:20 there are 10 minutes so I took 6:20 AM.
6. Now add all the minutes 5+30+10=45 minutes.
7. The start time is 6:20 AM.

Question 5.
3 hours after 1 0:25 A.M. ______________
Answer: 1:25 PM
Explanation:

Explanation:
1. Now I calculated the end time.
2. I wrote the start time on the timeline that is 10:25 AM.
3. I subtracted the 25 minutes of 10:25 AM from the 60 minutes to get 35 minutes. There are 35 minutes from 10:25 am and 11:05 am.
4. Between 11:05 am and 12:05 pm there is 1 hour.
5. Between 12:05 to 1:05 PM there is 1 hour.
6. Between 1:05 Pm to 1:30 Pm there is 25 minutes.
7. add all the hours1 hour+1 hour=2 hours.
8. Now add minutes 35 min+25 min=60 min which is equal to 1 hour.
9. Finally, 3 hours. The 10:25 after 3 hours is 1:30 PM.

Question 6.
2 hours before 1:20 P.M. ______________
Answer:11:15 AM
Explanation:

1. Already given end time that is 1:20 PM. We need to calculate the start time means before 2 hours.
2. We subtracted 20 min of 1:20 PM from the 60 minutes to get 40 min. So we calculated the difference of 40 min we get the time of 12:35 PM.
3. We calculated for 20 min because from their 1 hour will be completed. So we had taken 12:15. From 12:15 to 12:35 there is 1 hour.
4. And from 12:15 Pm to 11:15 AM there is 1 hour.
5. Finally we calculated for 2 hours. The start time is 11:15 AM.

Find the elapsed time. Draw a timeline to help you.

Example

Question 7.
7:45 P.M. to 8:15 P.M. _____________
Answer: 30 minutes.
Explanation:

1. The start time and end times are labelled at the end of the timeline.
2. Between 7:45 PM and 8:15 PM are the hours of half an hour which is marked on the timeline.
3. We subtract the 45 min of 7:45 PM from the 60 min to get 15 min. There are 15 minutes from 7:45 PM to 8:00 PM.
4. From 8:00 PM to 8:15 PM there are 15 minutes.
5. We add the minutes together. 15+15=30 minutes.
6. The elapsed time is 30 minutes.

Question 8.
2:30 P.M. to 4:50 P.M. _______________
Answer: 2 hours 20 minutes.
Explanation:

1. The start time and end times are labelled at the end of the timeline.
2. Between 2:30 PM and 4:50 PM are the hours of 3:00 and 4:00 PM which are marked on the timeline.
3. We subtract 30 min of 2:30 from the 60 min to get 30 min. There are 30 minutes from 2:30 and 3:00 PM.
4. Between 3:00 and 4:00 there is 1 hour.
5. Between 4:00 and 4:50 there are 50 minutes.
6. Adding minutes together. 30+50=80. Such that, we already know, 1 hour=60 minute. So, we can say 80 minutes is nothing but 1 hour 20 minutes.       (80-60=20)
7. Now by adding hours 1+1=2 hours.
8. Hence the resultant is 2 hour 20 minutes.

Find the elapsed time. Draw a time line to help you.

Question 9.
7:45 A.M. to 9:50 A.M _______________
Answer: 2 hours 5 minutes.
Explanation:

1. The start time and end times are labelled at the end of the timeline.
2. Between 7:45 AM and 9:50 AM are the hours of 8:00 and 9:00 AM which are marked on the timeline.
3. We subtract 45 min of 7:45 from the 60 min to get 15 min. There are 15 minutes from 7:45 and 8:00 AM.
4. Between 8:00 and 9:00 there is 1 hour.
5. Between 9:00 and 9:50 there are 50 minutes.
6. Adding minutes together. 15+50=65. Such that, we already know, 1 hour=60 minute. So, we can say 80 minutes is nothing but 1 hour 5 minutes.       (65-60=5)
7. Now by adding hours 1+1=2 hours.
8. Hence the resultant is 2 hours 5 minutes.

Question 10.
11:30 P.M. to 2:10 A.M. _______________
Answer:2 hour 40 minutes.

Explanation:
1. The start time and end times are labelled at the end of the timeline.
2. Between 11:30 PM and 2:10 AM are the hours of 12:00, 1:00, 2:00 AM which are marked on the timeline.
3. We subtract 30 min of 11:30 from the 60 min to get 30 min. There are 30 minutes from 11:30 and 12:00 AM.
4. Between 12:00 and 1:00 there is 1 hour.
5. Between 1:00 and 2:00 there is 1 hour.
6. Between 2:00 and 2:10 there are 10 minutes.
7. Adding minutes together. 10+30=40.
8. Now by adding hours 1+1=2 hours.
9. Hence the resultant is 2 hours 40 minutes.

Question 11.
11:25 A.M. to 3:10 P.M. _______________
Answer:3 hour 45 minutes.
Explanation:

1. The start time and end times are labelled at the end of the timeline.
2. Between 11:25 AM and 12:00 PM are the hours of 12:00, 1:00, 2:00, 3:00 PM which are marked on the timeline.
3. We subtract 25 min of 11:25 from the 60 min to get 35 min. There are 35 minutes from 11:25 and 12:00 PM.
4. Between 12:00 and 1:00 there is 1 hour.
5. Between 1:00 and 2:00 there is 1 hour.
6. Between 2:00 and 3:00 there is 1 hour.
7. Between 3:00 and 3:10 there are 10 minutes
7. Adding minutes together. 10+35=45.
8. Now by adding hours 1+1+1=3 hours.
9. Hence the resultant is 3 hours 45 minutes.

Write the correct time. Draw the missing hands on each clock.

Question 12.

Answer: 12:45 Am


1. Start time is given and need to calculate the end time.
2. 3 hours 15 minutes after the time is 12:45.
3. From 9:30 PM to 10:30 Pm there is 1 hour.
4. Between 10:30 PM to 11:30 Pm there is 1 hour.
5. Between 11:30 to 12:30 PM there is 1 hour.
6. Between 12:30 to 12:45 there is 15 minutes.
7. Adding hours we get 1+1+1=3 hours.
8. The minutes are 15 minutes.
9. Hence resultant is 3 hours 15 minutes that is 12:45.

Question 13.

Answer:11:15 PM


Explanation:
1. We already know the end time that is 2:00 AM
2. We need to calculate the elapsed time, 2 hours and 45 minutes.
3. Between 2:00 to 1:00 there is 1 hour.
4. Between 1:00 to 12:00 there is 1 hour.
5. 12:00 to 11:15 there are 45 minutes.
6. So I had taken 11:45 PM for 12:00 AM to 45 minutes.

Solve. Draw a timeline to help you.

Question 14.
Suki exercises every morning. She starts at 6:30 A.M. and ends at 8:15 A.M. How long does she exercise?

Answer: 1 hour 45 minutes.
Starting time=6:30 AM
Ending time=8:15 AM

1. The start time and end times are labelled at the end of the timeline.
2. Between 6:30 AM and 8:15 AM are the hours of 7:00, 8:00 AM which are marked on the timeline.
3. We subtract 30 min of 6:30 from the 60 min to get 30 min. There are 30 minutes from 6:30 and 7:00 AM.
4. Between 7:00 and 8:00 there is 1 hour.
5. Between 8:00 and 8:15 there is 15 minutes.
7. Adding minutes together. 15+30=45.
9. Hence the resultant is 1 hour 45 minutes.
Explanation:

Question 15.
Devon started reading a book at 2:35 P.M. She took 3 hours 10 minutes to finish the book. What time did she finish reading the book?

Answer:5:45 PM
Starting time=2:35 PM
Ending time=X
The given time=3 h 10 min.

Explanation:
1. The start time is labelled on the timeline that is 2:35 PM
2. Subtract 35 minutes of 2:35 from 60 minutes to get 25 min. There is 25 min from 2:35 and 3:00 PM.
3. From there we need to calculate 3 h 10 min after time.
4. Start from 3:00 PM, between 3:oo PM to 4:00 PM there is 1 hour.
5. Between 4:00 PM to 5:00 PM there is 1 hour.
6. Between 5:00 PM to 5:35 PM there are 35 minutes.
7. Between 5:35 to 5:45 there are 10 minutes.
8. Likewise we need to calculate the ending time.
9. Adding all the minutes:25+35+10=70 minutes. We can write 70 as 1 hour 10 minutes. (1 hour=60 minutes).
10. Finally, the result of 3 h 10 min is 5:45 PM.

Question 16.
Lissa went to the library. She was there for 2 hours 15 minutes. She left the library at 5:40 P.M. What time did she get to the library?
Answer:
We need to calculate starting time.
We can say it as another way 2 hours 15 minutes before 5:40 PM.

Explanation:
1. The end time is labelled on the timeline that is 5:40 PM
2. Subtract 40 min of 5:40 from 60 min to get 20. The 20 min before 5:40 is 5:20 PM.
3. Now calculate for 1 hour that is 5:20 to 4:20.
4. Now we need to calculate for 55 minutes. The 55 minutes before 4:20 is 3:25 PM.

Question 17.
Marcus visited his friend’s house from 11:50 A.M. to 3:15 P.M. How long was his visit?

Answer: 3 h 25 min
Starting time=11:50 AM
Ending time=3:15 PM

1. The start time and end times are labelled at the end of the timeline.
2. Between 11:50 AM and 12:00 PM are the hours of 12:00, 1:00, 2:00, 3:00 PM which are marked on the timeline.
3. We subtract 50 min of 11:50 from the 10 min to get 10 min. There are 10 minutes from 11:50 and 12:00 PM.
4. Between 12:00 and 1:00 there is 1 hour.
5. Between 1:00 and 2:00 there is 1 hour.
6. Between 2:00 and 3:00 there is 1 hour.
7. Between 3:00 and 3:15 there are 15 minutes
7. Adding minutes together. 10+15=25.
8. Now by adding hours 1+1+1=3 hours.
9. Hence the resultant is 3 hours 25 minutes.

Question 18.
Mr. Nelson took 3 hours 30 minutes to decorate his classroom. He started at 9:20 A.M. What time did he finish?

Answer: 12:45 PM
Starting time=9:20 AM
The elapsed time is given: 3 h 30 min.
Ending time=X

Explanation:
1. I labelled starting time on the timeline that is 9:20 AM
2. Subtract 20 min of 9:20 from the 60 min to get 60-20=40.
4. And from there, calculate according to the elapsed time.
5. Now calculate for 3 hours and then calculate for 30 minutes.
6. Now observe the above timeline in which we represented all the calculations.
7. Finally, the end time is 12:45 PM.

Question 19.
Mrs Martin’s flight landed at 2:25 A.M. The flight was 4 hours 45 minutes long. What time did the flight take off?

Answer:  7:10 AM
Starting time=2:25 AM
Elapsed time=4 h 45 min
Ending time=X

Explanation:
1. I labelled starting time on the timeline that is 2:25 AM
2. Subtract 25 min of 2:25 from the 60 min to get 60-25=35.
4. And from there, calculate according to the elapsed time.
5. Now calculate for 4 hours and then calculate for 1o minutes because we calculated already 35 minutes.
6. Now observe the above timeline in which we represented all the calculations.
7. Finally, the end time is 7:10 AM.

Must Read:

Banknifty Pivot Point

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 16 Practice 4 Subtraction of Time provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 16 Practice 4 Answer Key Subtraction of Time

Subtract

Example

Question 1.

So, 8 h 20 min – 7 h 15 min
= _______ h _________ min.

______ h – ______ h = ______ h
______ min – ______ min = ______ min
______ h – ______ min = ______ h ______ min
Answer: 1 hour 5 minutes.
We measure time in hours, minutes, and seconds. There are 60 minutes in an hour and 60 seconds in a minute.
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Explanation:
Step 1: Subtract the hours.
=8hours-7hours
=1 hour
Step 2: Subtract the minutes.
=20min-15min
=5 min
Hence, the resultant from Step 1 and Step 2 together is the answer (1hour 5minutes).

Question 2.

So, 4 h 35 min – 1 h 15 min
= _______ h _________ min.

______ h – ______ h = ______ h
______ min – ______ min = ______ min
______ h – ______ min = ______ h ______ min
Answer:3 hour 20 minutes
We measure time in hours, minutes, and seconds. There are 60 minutes in an hour and 60 seconds in a minute.
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Explanation:
Step 1: Subtract the hours.
=4hours-1hours
=3 hour
Step 2: Subtract the minutes.
=35min-15min
=20 min
Hence, the resultant from Step 1 and Step 2 together is the answer (3hour 20minutes).

Question 3.

So, 3 h 55 min – 2 h 30 min
= _______ h _________ min.

______ h – ______ h = ______ h
______ min – ______ min = ______ min
______ h – ______ min = ______ h ______ min
Answer: 1 hour 25 minutes.
We measure time in hours, minutes, and seconds. There are 60 minutes in an hour and 60 seconds in a minute.
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Explanation:
Step 1: Subtract the hours.
=3hours-2hours
=1 hour
Step 2: Subtract the minutes.
=55min-30min
=25 min
Hence, the resultant from Step 1 and Step 2 together is the answer (1hour 25minutes).

Subtract

Question 4.

Answer: 30 minutes
Explanation:
We measure time in hours, minutes, and seconds. There are 60 minutes in an hour and 60 seconds in a minute.
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Here in the question, 2 h 20 min and 1 h 50 min.
Explanation:
Step 1: Subtract the hours.
=2hours-1hours
=1 hour
Step 2: Subtract the minutes.
=20min-50min
=-30 min
The minutes are negative. So follow step 3.
Step 3: add 60 to the minutes and subtract 1 from hours.
=60+20
=80
Subtract 1 from 2
=2-1
=1
Now calculate 1 h 80 min and 1 h 50 min
If we subtract hours 1-1=0
If we subtract min 80-50=30
Hence, the resultant from Step 1 and Step 2 together is the answer (0hour 30minutes).

Question 5.

Answer: 2 h 50 min

Explanation:
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Here in the question, 2 h 20 min and 1 h 50 min.
Explanation:
Step 1: Subtract the hours.
=5hours-2hours
=3 hour
Step 2: Subtract the minutes.
=15min-25min
=-10 min
The minutes are negative. So follow step 3.
Step 3: add 60 to the minutes and subtract 1 from hours.
=60+15
=75
Subtract 1 from 2
=5-1
=4
Now calculate 4 h 75 min and 2 h 25 min
If we subtract hours 4-2=2
If we subtract min 75-25=50
Hence, the resultant from Step 1 and Step 2 together is the answer (2hour 50minutes).

Question 6.

Answer:4 h 15 min

Explanation:
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Here in the question, 6 h 10 min and 1 h 55 min.
Explanation:
Step 1: Subtract the hours.
=6hours-1hours
=5 hour
Step 2: Subtract the minutes.
=10min-55min
=-45 min
The minutes are negative. So follow step 3.
Step 3: add 60 to the minutes and subtract 1 from hours.
=10+60
=70
Subtract 1 from 6
=6-1
=5
Now calculate 5 h 70 min and 1 h 55 min
step 4: If we subtract hours 5-1=4
step 5: If we subtract min 70-55=15
Hence, the resultant from Step 4 and Step 5 together is the answer (4hour 15minutes).

Question 7.

Answer: 4 h 55 min

Explanation:
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Here in the question, 9 h 40 min and 4 h 45 min.
Explanation:
Step 1: Subtract the hours.
=9hours-4hours
=5 hour
Step 2: Subtract the minutes.
=40min-45min
=-5 min
The minutes are negative. So follow step 3.
Step 3: add 60 to the minutes and subtract 1 from hours.
=40+60
=100
Subtract 1 from 9
=9-1
=8
Now calculate 8 h 100 min and 4 h 45 min
step 4: If we subtract hours 8-4=4
step 5: If we subtract min 100-45=55
Hence, the resultant from Step 4 and Step 5 together is the answer (4hour 55minutes).

Solve.

Question 8.
Rita takes 3 hours 5 minutes to sew a dress. Tara takes 2 hours 40 minutes to sew a similar dress. How much longer does Rita take to sew the dress than Tara?
Answer: 25 minutes longer Tita take to sew the dress than Tara.
The time Rita takes to sew a dress=3 h 5 minutes.
The time Tara takes to sew a dress=2 h 40 minutes.
Follow these steps:
1. Subtract the hours
2. Subtract the minutes
3. If the minutes are negative, add 60 to the minutes and subtract 1 from hours.
Here in the question, 3 h 5 min and 2 h 40 min.
Explanation:
Step 1: Subtract the hours.
=3hours-1hours
=1 hour
Step 2: Subtract the minutes.
=5min-40min
=-35 min
The minutes are negative. So follow step 3.
Step 3: add 60 to the minutes and subtract 1 from hours.
=60+5
=65
Subtract 1 from 3
=3-1
=2
Now calculate 2 h 65 min and 2 h 40 min
step 4: If we subtract hours 2-2=0
step 5: If we subtract min 65-40=25
Hence, the resultant from Step 4 and Step 5 together is the answer (0hour 25minutes).

Must Try:

Pivot Point Calculator

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Cumulative Review Chapters 5 and 6 to score better marks in the exam.

Math in Focus Grade 4 Cumulative Review Chapters 5 and 6 Answer Key

Concepts and Skills
Complete. Use the data in the table. (Lesson 5.1)

The ages of four cousins are shown.
8, 12, 10, 6

Question 1.
The sum of their ages is ___ years.
Answer:
Sum of their ages = 36 years.

Explanation:
The ages of four cousins are shown.
8, 12, 10, 6
Sum of their ages = 8 + 12 + 10 + 6
= 20 + 10 + 6
= 30 + 6
= 36 years.

 

Question 2.
The mean age of the cousins is ___ years.
Answer:
Mean age of their ages = 9 years.

Explanation:
The mean is the average of the numbers. It is easy to calculate: add up all the numbers, then divide by how many numbers there are.
Sum of their ages = 36 years.
Number of people = 4.
Mean age of their ages = Sum of their ages ÷ Number of people
= 36 ÷ 4
= 9 years.

 

Answer each question. Use the data in the line plot. (Lesson 5.2)
A group of hikers made a line plot to show the number of mountains they climbed. Each ✗ represents one hiker.

Question 3.
What is the median number of mountains climbed? ____
Answer:
Median number of mountains climbed = 4.

Explanation:
Number of mountain hikers = 1 1 1 2 3 3 3 3 4 4 5 5 5 6 6 6 6 6
Median number of mountains climbed = (4 + 4) ÷ 2
= 8 ÷ 2
= 4.

 

Question 4.
What is the range of the set of data? ____
Answer:
The range of the set of data = 1 to 6.

Explanation:
The range of a set of data is the difference between the highest and lowest values in the set.
Number of mountain hikers = 1 1 1 2 3 3 3 3 4 4 5 5 5 6 6 6 6

 

Question 5.
What is the mode of the set of data? ____
Answer:
The mode of the set of data = 6.

Explanation:
The mode is the value that appears most often in a set of data values.
1 mountain climbed by 3 people.
2 mountain climbed by 1 person.
3 mountain climbed by 4 people.
4 mountain climbed by 2 people.
5 mountain climbed by 3 people.
6 mountain climbed by 5 people.

 

Make a stem-and-leaf plot to show the data. (Lesson 5.3)
Question 6.
A group of friends went bowling and recorded these scores.
75 73 79 84 98 64 84 67

Answer:

Explanation:
Arrange the scores given: 64 67 73 75 79 84 84 98.
To make a stem and leaf plot, each observed value must first be separated into its two parts:

Complete. Use the data in your stem-and-leaf plot.
Question 7.
____ is the mode.
Answer:
84 is the mode.

Explanation:
Scores given: 64 67 73 75 79 84 84 98.
64 – 1
67 – 1
73 – 1
75 – 1
79 – 1
84 – 2
98 – 1.

 

Question 8.
___ is the median.
Answer:
77 is the median.

Explanation:
Scores given: 64 67 73 75 79 84 84 98.
Median = (75 + 79) ÷ 2
= 154 ÷ 2
= 77.

 

Question 9.
___ is the range.
Answer:
64 to 98 is the range.

Explanation:
Scores given: 64 67 73 75 79 84 84 98.

 

Question 10.
___ is an outlier.
Answer:
84 to 98 is an outlier.

Explanation:
84 – 79 = 5.
73 – 67 = 6.
98 – 84 = 14.

 

Question 11.
How do the mode and median each change if you disregard the outlier?
Answer:
The effect of removing one outlier data point from the set. No matter what value we add to the set, the mean, median, and mode will shift by that amount but the range and the IQR will remain the same.

Explanation:
Outlier is an extreme value in a set of data which is much higher or lower than the other numbers. Outliers affect the mean value of the data but have little effect on the median or mode of a given set of data.

Write more likely, less likely, equally likely, certain, or impossible. (Lesson 5.4)
A bag has 8 blue marbles and 2 orange marbles. Describe the likelihood of each outcome.
Question 12.
An orange marble is chosen. _____
Answer:
Probability of orange marbles is chosen = 1 ÷ 5 or \(\frac{1}{5}\) .

Explanation:
Number of blue marbles = 8.
Number of orange marbles = 2.
Total marbles in bag = 8 + 2 = 10.
Probability of orange marbles is chosen = Number of orange marbles ÷ Total marbles in bag
= 2 ÷ 10
= 1 ÷ 5 or \(\frac{1}{5}\) .

 

Question 13.
A blue marble is chosen. ____
Answer:
Probability of blue marbles is chosen = 4 ÷ 5 or \(\frac{4}{5}\) .

Explanation:
Number of blue marbles = 8.
Number of orange marbles = 2.
Total marbles in bag = 8 + 2 = 10.
Probability of blue marbles is chosen = Number of blue marbles ÷ Total marbles in bag
= 8 ÷ 10
= 4 ÷ 5 or \(\frac{4}{5}\) .

Question 14.
A red marble is chosen. ____
Answer:
Probability of red marbles is chosen = 0.

Explanation:
Number of blue marbles = 8.
Number of orange marbles = 2.
Number of red marbles = 0.
Total marbles in bag = 8 + 2 = 10.
Probability of red marbles is chosen = Number of red marbles ÷ Total marbles in bag
= 0 ÷ 10
= 0.

 

Question 15.
A blue or an orange marble is chosen. ____
Answer:
Probability of orange or blue marbles is chosen = 1.

Explanation:
Number of blue marbles = 8.
Number of orange marbles = 2.
Total marbles in bag = 8 + 2 = 10.
Probability of blue marbles is chosen = Number of blue marbles ÷ Total marbles in bag
= 8 ÷ 10
= 4 ÷ 5 or \(\frac{4}{5}\) .
Probability of orange marbles is chosen = Number of orange marbles ÷ Total marbles in bag
= 2 ÷ 10
= 1 ÷ 5 or \(\frac{1}{5}\) .
Probability of orange or blue marbles is chosen = (Number of orange marbles + Number of blue marbles) ÷ Total marbles in bag)
= (8 + 2) ÷ 10
= 10÷ 10
= 1.

Solve. Use the scenario above. (Lesson 5.4)
Question 16.
How would you change the number of each colored marble in the bag so that it is more likely that an orange marble is chosen?
Answer:

Explanation:
Number of blue marbles = 8.
Number of orange marbles = 2.
Total marbles in bag = 8 + 2 = 10.

 

Look at the spinner. Write the probability of each outcome as a fraction. (Lesson 5.5)

Question 17.
Probability of landing on 2 = ____
Answer:
Probability of landing on 2 = 2 ÷ 3 or \(\frac{2}{3}\)

Explanation:
Number of 2 on spinner = 4.
Total numbers on spinner = 6.
Probability of landing on 2 = Number of 2 on spinner ÷ Total numbers on spinner
= 4 ÷ 6
= 2 ÷ 3 or \(\frac{2}{3}\)

 

Question 18.
Probability of landing on 6 = ____
Answer:
Probability of landing on 6 = 0.

Explanation:
Number of 6 on spinner = 0.
Total numbers on spinner = 6.
Probability of landing on 6 = Number of 6 on spinner ÷ Total numbers on spinner
= 0 ÷ 6
= 0.

 

Add or subtract. Write each answer in simplest form. (Lessons 6.1 and 6.2)
Question 19.
\(\frac{3}{4}\) + \(\frac{1}{12}\) + \(\frac{1}{6}\) =
Answer:
\(\frac{3}{4}\) + \(\frac{1}{12}\) + \(\frac{1}{6}\) = \(\frac{11}{12}\)

Explanation:
\(\frac{3}{4}\) + \(\frac{1}{12}\) + \(\frac{1}{6}\) =
= [(9 + 1) ÷ 12] + \(\frac{1}{12}\)
= \(\frac{10}{12}\) + \(\frac{1}{12}\)
= (10 + 1) ÷ 12
= \(\frac{11}{12}\)

 

Question 20.
\(\frac{9}{10}\) – \(\frac{1}{5}\) – \(\frac{1}{2}\) =
Answer:
\(\frac{9}{10}\) – \(\frac{1}{5}\) – \(\frac{1}{2}\) = \(\frac{1}{5}\)

Explanation:
\(\frac{9}{10}\) – \(\frac{1}{5}\) – \(\frac{1}{2}\) =
= [(9 – 2) ÷ 10] – \(\frac{1}{2}\)
= \(\frac{7}{10}\) – \(\frac{1}{2}\)
= (7 – 5) ÷ 10
= 2 ÷ 10
= \(\frac{1}{5}\)

 

Write the amount of water in each set of 1-liter containers as a mixed number. (Lesson 6.3)
Question 21.

Answer:
Amount of 2 jars = 1 \(\frac{1}{5}\)L.

Explanation:
Amount of water in first jar = 1L.
Amount of water in second jar = \(\frac{1}{5}\)L.
Amount of 2 jars = Amount of water in first jar + Amount of water in second jar
= 1 + \(\frac{1}{5}\)
= (5 + 1) ÷ 5
= \(\frac{6}{5}\)
= 1 \(\frac{1}{5}\)L.

Question 22.

Answer:
Amount of three jars = 2\(\frac{1}{2}\)L.

Explanation:
Amount of water in first jar = 1L.
Amount of water in second jar = 1L.
Amount of water in third jar = \(\frac{1}{2}\)L.
Amount of three jars = Amount of water in first jar + Amount of water in second jar + Amount of water in third jar
= 1 + 1 + \(\frac{1}{2}\)
= 2 + \(\frac{1}{2}\)
= (4 + 1) ÷ 2
= \(\frac{5}{2}\)
= 2\(\frac{1}{2}\)L.

Express the shaded part of each figure as a mixed number or an improper fraction. (Lessons 6.4 and 6.5)
Question 23.

Answer:

Explanation:
Mixed number of the shaded figure = 2\(\frac{3{4}\)
Improper fraction of the shaded figure = (8 + 3) ÷ 4
= 11 ÷ 4 or \(\frac{11}{4}\)

 

Question 24.

Answer:

Explanation:
Improper fraction of the shaded figure = \(\frac{12}{8}\)
Mixed number of the shaded figure = \(\frac{12}{8}\)
= 1\(\frac{4}{8}\)

Express each improper fraction as a mixed number. (Lesson 6.5)
Question 25.
\(\frac{9}{7}\) = ____
Answer:
\(\frac{9}{7}\) = 1\(\frac{2}{7}\)

Explanation:
\(\frac{9}{7}\) = 1\(\frac{2}{7}\)

 

Question 26.
\(\frac{20}{9}\) = ____
Answer:
\(\frac{20}{9}\) = 2\(\frac{2}{9}\)

Explanation:
\(\frac{20}{9}\) = 2\(\frac{2}{9}\)

 

Express each mixed number as an improper fraction. (Lesson 6.5)
Question 27.
3\(\frac{2}{5}\) = ____
Answer:
3\(\frac{2}{5}\) = \(\frac{17}{5}\)

Explanation:
3\(\frac{2}{5}\) = (15 + 2 ) ÷ 5 = \(\frac{17}{5}\)

 

Question 28.
2\(\frac{8}{9}\) = ____
Answer:
2\(\frac{8}{9}\) = \(\frac{26}{9}\)

Explanation:
2\(\frac{8}{9}\) = (18 + 8) ÷ 9 = \(\frac{26}{9}\)

 

Add or subtract. (Lesson 6.6)
Question 29.
2 + \(\frac{2}{5}\) + \(\frac{1}{10}\) = ____
Answer:
2 + \(\frac{2}{5}\) + \(\frac{1}{10}\) = \(\frac{25}{10}\)

Explanation:
2 + \(\frac{2}{5}\) + \(\frac{1}{10}\) = ](10 + 2) 5] + \(\frac{1}{10}\)
= \(\frac{12}{5}\) + \(\frac{1}{10}\)
= (24 + 1) ÷ 10
= \(\frac{25}{10}\)

Question 30.
3 – \(\frac{3}{4}\) – \(\frac{5}{8}\) = ___
Answer:
3 – \(\frac{3}{4}\) – \(\frac{5}{8}\) = \(\frac{23}{8}\)

Explanation:
3 – \(\frac{3}{4}\) – \(\frac{5}{8}\) = 3 – [(6 – 5)÷ 8]
= 3 – \(\frac{1}{8}\)
= (24 – 1) ÷ 8
= \(\frac{23}{8}\)

 

check (✓) each set in which \(\frac{2}{5}\) of the figures are shaded. (Lesson 6.7)
Question 31

Answer:

Explanation:
(✓) each set in which \(\frac{2}{5}\) of the figures are shaded.
Fraction of square figure = Number of shaded squares ÷ Total number of squares
= 8 ÷ 16
= 1 ÷ 2 or \(\frac{1}{2}\)
Fraction of circle figure = Number of shaded circles ÷ Total number of circles
= 6 ÷ 15
= 2 ÷ 5 or \(\frac{2}{5}\)
Fraction of triangle figure = Number of shaded triangles ÷ Total number of triangles
= 4 ÷ 20
= 1 ÷ 5 or \(\frac{1}{5}\)

 

Solve. (Lesson 6.7)
Question 32.
\(\frac{2}{3}\) of 15 = ___
Answer:
\(\frac{2}{3}\) of 15 = 10.

Explanation:
\(\frac{2}{3}\) of 15 = 2 ×5 = 10.

 

Question 33.
\(\frac{3}{5}\) of 40 = ___
Answer:
\(\frac{3}{5}\) of 40 = 24.

Explanation:
\(\frac{3}{5}\) of 40 = 3 × 8 = 24.

 

Problem Solving
Solve. Show your work.
Question 34.
Teams A, B, C, and D were in a tournament. The average score of the 4 teams was 92. Team A scored 78 points,
Team B scored 95 points, and Team C scored 88 points.

a. How many points did Team D score?
Answer:
Points Team D scored = 107.

Explanation:
Points Team A scored = 78.
Points Team B scored = 95.
Points Team C scored = 88.
Points Team D  scored = ??.
The average score of the 4 teams was 92.
=> (Points Team A scored + Points Team B scored + Points Team C scored  + Points Team D scored) ÷ 4 = 92.
=> (78 + 95 + 88 + ??) ÷ 4 = 92.
=> (173 + 88 + ??) ÷ 4 = 92.
=> (261 + ??) ÷ 4 = 92 × 4
=> 261 + ?? = 92 × 4
=> 261 + ?? = 368.
=> ?? = 368 – 261
=> ?? = 107.
Points Team D scored = 107.

 

b. Find the range of the scores. Hence, state the difference in score between the winning team and the losing team.
Answer:
Range of the scores = 78 to 107.
29 is the difference in score between the winning team and the losing team.

Explanation:
Scores scored by teams = 78 88 95 107.
Points Team A scored = 78.
Points Team B scored = 95.
Points Team C scored = 88.
Points Team D  scored = 107.
Difference:
Highest score scored – Least score scored
= 107 – 78
= 29.
Losing team are Team A,B,C. Winning team is A.

 

Question 35.
Michael scored 15, 21, and 24 in the first three basketball games of the season.
a. What is his mean score?
Answer:
His mean score = 20.

Explanation:
Score scored by Michael in the first three basketball games of the season = 15, 21, 24.
The mean is the arithmetic average of a set of given numbers. The median is the middle score in a set of given numbers. The mode is the most frequently occurring score in a set of given numbers.
His mean score = score scored ÷ Number of games
= (15 + 21 + 24) ÷ 3
= (36 + 24) ÷ 3
= 60 ÷ 3
= 20.

 

b. What is the range of his scores?
Answer:
Range of his scores = 15 to 24.

Explanation:
Score scored by Michael in the first three basketball games of the season = 15, 21, 24.
Range of his scores = 15 to 24.

c. How many points must he score in the next game to achieve a mean score of 27?
Answer:
48 more points must he score in the next game to achieve a mean score of 27.

Explanation:
His mean score = score scored ÷ Number of games
=> 27 = (15 + 21 + 24 + ?? ) ÷ 4
=> 27 = (36 + 24 + ?? ) ÷ 4
=> 27 = (60 + ?? ) ÷ 4
=> 27 × 4 = 60 + ??
=> 108 – 60 = ??
=> 48 = ??.

 

Question 36.
Samuel and Kenneth collect sports cards. The average number of cards they have is 248. Samuel has 3 times as many cards as Kenneth. How many cards does each boy have?
Answer:
Number of sports cards Kenneth collected = 124.
Number of sports cards Samuel collected = 372.

Explanation:
Samuel has 3 times as many cards as Kenneth.
Let Number of sports cards Kenneth collected be X.
=> Number of sports cards Samuel collected = 3 × Number of sports cards Kenneth collected
= 3  × X = 3X.
The average number of cards they have is 248.
=> (Number of sports cards Samuel collected + Number of sports cards Kenneth collected) ÷ 2 = 248.
=> (3X + X) ÷ 2 = 248
=> 4X ÷ 2 = 248.
=> 4X = 248 × 2
=> 4X = 496.
=> X = 496 ÷ 4
=> X = 124.
Number of sports cards Samuel collected = 3X = 3 × 124 = 372.

 

Question 37.
A group of students made a list of the states where they were born. The line plot shows the number of times the letter A’ appears in the name of each state. Each ✗ represents one state.

Complete. Use the data in the line plot.
a. What is the mode of the set of data? ____
Answer:
Mode of the set of data = 1.

Explanation:
Number of times A appears in states = 0 1 1 1 2 2 3 4 4
The mode is the most frequently occurring score in a set of given numbers.
Mode of the set of data = 1.

b. What is the mean number of times the letter A’ appears? ___
Answer:
Mean number of times the letter A’ appears = 2.

Explanation:
The mean is the arithmetic average of a set of given numbers.
Number of times A appears in states = 0 1 1 1 2 2 3 4 4
mean number of times the letter A’ appears = (0 + 1 + 1 + 1 + 2 + 2 + 3 + 4 + 4) ÷ 9
= 18 ÷ 9
= 2.

 

c. Is the name of a state more likely to have 1 or 2 As? Explain your answer.
Answer:
Yes, the state going to have more likely 2As because mean number of times the letter A’ appears = 2.

Explanation:
Yes state is going to have 2 As because average letters in the states name going to be 2 that menas in their names 2As are likely to be.

 

d. According to the data, what is less likely to happen? Explain your answer.
Answer:
According to the data, its less likely to happen that minimum As likely to be 1 and maximum 2 As in every name of state not more.

Explanation:
Well, its less likely to happen that minimum As likely to be 1 and maximum 2 As in every name of state not more.

Question 38.
The stem-and-leaf plot shows the number of pages in 8 books.

a. Which stem has only odd numbers for its leaves?
Answer:
Stem 3 is having only odd numbers for its leaves.

Explanation:
All the numbers ending with 1,3,5,7 and 9 are odd numbers. For example, numbers such as 11, 23, 35, 47 etc.
Stem 2 – 1 5
Stem 3 – 0 5 5 7.
Stem 4 – 3 6.

 

b. Find the median of the set of data.
Answer:
Median of set = 35.

Explanation:

Number of pages = 21, 25, 30, 35, 35, 37, 43, 46.
Median of set = (35 + 35) ÷ 2
= 70 ÷ 2
= 35.

 

c. Find the mode of the set of data. ___
Answer:
Mode of the set of data = 35.

Explanation:
The mode is the value that appears most often in a set of data values.
Number of pages = 21, 25, 30, 35, 35, 37, 43, 46.

21 – 1 time.
25 – 1 time.
30 – 1 time.
35 – 2 time.
37 – 1 time.
43 – 1 time.
46 – 1 time.

 

d. Find the range of the set of data. ____
Answer:
Range of the set of data – 21 to 46.

Explanation:
Number of pages = 21, 25, 30, 35, 35, 37, 43, 46.

 

e. Which of the above measures tells you the difference in the number of pages between the thickest and the thinnest books? ___
Answer:
Range of the set of data above measures tells you the difference in the number of pages between the thickest and the thinnest books.

Explanation:
Range of the set of data above measures tells you the difference in the number of pages between the thickest and the thinnest books.

 

f. Is there an outlier in the set of data? Explain your answer. ___
Answer:
No, there is no outlier in the set of data because there is no much difference in the data measurements.

Explanation:
There is no outlier in the set of data because there is no much difference in the data measurements.

 

Question 39.
A cube is numbered from 1 to 6 and tossed once. What is the probability of tossing
a. a 5 or a 6? ___
Answer:
Probability of tossing 5 = 1 ÷ 6 or \(\frac{1}{6}\)
Probability of tossing 6 = 1 ÷ 6 or \(\frac{1}{6}\)

Explanation:
A cube is numbered from 1 to 6 and tossed once.
Total numbers on cube = 6.
Probability of tossing 5 = Number of 5 side ÷ Total numbers on cube
= 1 ÷ 6 or \(\frac{1}{6}\)
Probability of tossing 6 = Number of 6 side ÷ Total numbers on cube
= 1 ÷ 6 or \(\frac{1}{6}\)

b. an odd number? ___
Answer:
Probability of odd number = 1 ÷ 2 or \(\frac{1}{2}\)

Explanation:
odd number on cube = 1, 3 , 5.
Total numbers on cube = 6.
Probability of odd number = odd number on cube ÷ Total numbers on cube
= 3 ÷ 6
= 1 ÷ 2 or \(\frac{1}{2}\)

 

Question 40.
Sasha has 40 stamps in her collection. 12 of them are from foreign countries.

a. What fraction of the stamps are foreign stamps?
Answer:
Fraction of the stamps are foreign stamps = 3 ÷ 10 or  \(\frac{3}{10}\)

Explanation:
Number of stamps in her collection Sasha has = 40.
Number of stamps of them are from foreign countries = 12.
Fraction of the stamps are foreign stamps = Number of stamps of them are from foreign countries ÷ Number of stamps in her collection Sasha has
= 12 ÷ 40
= 3 ÷ 10 or  \(\frac{3}{10}\)

 

b. What fraction of the stamps are U.S. stamps?
Answer:
3 ÷ 10 or  \(\frac{3}{10}\)  are fraction of the stamps are U.S. stamps.

Explanation:
Fraction of the stamps are U.S. stamps = Number of stamps of them are from U.S.  countries ÷ Number of stamps in her collection Sasha has
= 12 ÷ 40
= 3 ÷ 10 or  \(\frac{3}{10}\)

 

Question 41.
A string is 1 foot long. Blake cuts What fraction of the string is left?
Answer:

Explanation:
Length of the string = 1 foot.

 

Question 42.
Pedro scored \(\frac{1}{4}\) of all the goals scored during a soccer game. He scored 2 goals. How many goals were not scored by Pedro?
Answer:
Number of goals were not scored by Pedro = 6.

Explanation:
Points scored by Pedro \(\frac{1}{4}\) of all the goals scored during a soccer game.
Let all goals be X.
Points soccer game scored = X × \(\frac{1}{4}\) = 2.
=> X = 2 × 4
=> X = 8.
Points Pedro scored = 2.
Number of goals were not scored by Pedro = Points soccer game scored – Points Pedro scored
= 8 – 2
= 6.

Must Follow:

MCX Pivot Point Calculator

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 15 Practice 1 Measuring Length provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 15 Practice 1 Answer Key Measuring Length

Measure each to the nearest inch.

Example

Question 1.

Answer:

Explanation:
In the above image we can observe Ruler and Rope B. The length of the Rope B is calculated by using Ruler.
The length of rope B is more than 4 inches but less than 5 inches long. It is nearer to 4 inches than to 5 inches. So, the length of Rope B is about 4 inches.

Question 2.

Rope C is about ___________ inches.
Answer:

Explanation:
In the above image we can observe Ruler and Rope C. The length of the Rope C is calculated by using Ruler.
The length of rope C is more than 1 inch long. It is nearer to 2 inches than 1 inch. So, the length of Rope C is about 2 inches.

Question 3.

Rope D is about ___________ inches.
Answer:

Explanation:
In the above image we can observe Ruler and Rope D. The length of the Rope D is calculated by using Ruler.
The length of rope D is in between 2 and 3 inches. So, the length of Rope D is about 2.5 inches.

Measure each ribbon to the nearest half-inch.

Example

Question 4.

Ribbon B is about __________ inches long.
Answer:

Explanation:
In the above image we can observe Ruler and Ribbon B. The length of the Ribbon B is calculated by using Ruler.
The length of ribbon B is more than 3 1/2 inches. It is nearer to 4 inches than 3 inches. So, the length of Ribbon B is about 4 inches long.

Question 5.

Ribbon C is about __________ inches long.
Answer:

Explanation:
In the above image we can observe Ruler and Ribbon C. The length of the Ribbon C is calculated by using Ruler.
The length of Ribbon C is more than 2 inches but less than 2 1/2 inches. It is nearer to 2 1/2 inches than 2 inches. So, the length of Ribbon C is about 2 1/2 inches long.

Question 6.

Ribbon D is about __________ inches long.
Answer:

Explanation:
In the above image we can observe Ruler and Ribbon D. The length of the Ribbon D is calculated by using Ruler.
The length of Ribbon D is more than 5 1/2 inches but less than 6 inches. It is nearer to 6 inches than 5 1/2 inches. So, the length of Ribbon D is about 6 inches long.

Question 7.

Ribbon E is about __________ inches long.
Answer:

Explanation:
In the above image we can observe Ruler and Ribbon E. The length of the Ribbon E is calculated by using Ruler.
The length of Ribbon E is more than 4 1/2 inches but less than 5 inches. It is nearer to 5 inches than 4 1/2 inches. So, the length of Ribbon E is about 5 inches long.

Question 8.

Ribbon F is about __________ inches long.
Answer:

Explanation:
In the above image we can observe Ruler and Ribbon F. The length of the Ribbon F is calculated by using Ruler
The length of Ribbon F is more than 4 inches but less than 5 inches. It is at 4 1/2 inches. So, the length of Ribbon F is about 4.5 inches long.

Estimate the length of each object to the nearest half-inch.

Question 9.
Bracelet A is about _________ quarters long.
Answer:
Bracelet A is about 3 quarters long.

Question 10.
It is about ___________ inches long.
Answer:
It is about 3 inches long.
Explanation:
In the above image we can observe one quarter is 1 inch wide. There are 3 quarters. It is about 3 inches long.

Question 11.
Bracelet B is about ___________ quarters long.
Answer:
Bracelet B is about 5 quarters long.

Question 12.
It is about __________ inches long.
Answer:
It is about 5 inches long.
Explanation:
In the above image we can observe one quarter is 1 inch wide. There are 5 quarters. It is about 5 inches long.

Estimate the length of each object to the nearest half-inch.

Question 13.
Craft stick C is about ___________ buttons long.
Answer:
Craft stick C is about 3 buttons long.

Question 14.
It is about ___________ inches long.
Answer:
It is about 1 1/2 inches long.
Explanation:
In the above image we can observe one button is 1/2 inch wide. There are 3 buttons. It is about 1 1/2 inches long.

Estimate the length of each object to the nearest half-inch.

Question 15.
Craft stick D is about ___________ buttons long.
Answer:
Craft stick D is about 4 buttons long.

Question 16.
It is about ___________ inches long.
Answer:
It is about 2 inches long.
Explanation:
In the above image we can observe one button is 1/2 inch wide. There are 4 buttons. It is about 2 inches long.

Fill in the blanks. These are 12-inch rulers.

Question 17.
1 ft = ____________ in.
Answer:
1 feet = 12 inch

Question 18.
1 yd = ___________ ft = ___________ in.
Answer:
1 yard = 3 feet = 36 inches
Explanation:
In the above image we can observe 1 feet is equal to 12 inches. We know that 1 yard is equal to 3 feet.
3 x 12 = 36 inches
3 feet is equal to 36 inches.

Name 3 objects that are 1 foot long each.

Question 19.
The 3 items are ___________, ___________, and ___________.
Answer:

Name 3 objects that are longer than 1 foot but shorter than 3 feet.

Question 20.
___________, ___________, and ___________ are longer than 1 foot but shorter than 3 feet.
Answer:

Sarah is going on a treasure hunt. She is looking for objects that are about 3 feet long. 3 feet is equal to 1 yard.
Answer:

Look at the objects she has found. Then sort them in the table.

Question 21.

Answer:

Complete. Use the map to help you.

Question 22.
The distance between Camp Evergreen and Camp Birch is __________ mile.
Answer:
The distance between Camp Evergreen and Camp Birch is 1 mile.
Explanation:
In the above image we can observe the distance between Camp Evergreen and Camp Birch is 1,760 yard. We know that 1 mile is equal to 1,760 yard.

Question 23.
The distance between Camp Birch and the Bay Station is about __________ mile.
Answer:
The distance between Camp Birch and the Bay Station is about 1 mile.
Explanation:
The distance between camp Birch to camp plane is 5,170 feet.
The distance between camp plane to bay station is 107 feet.
5,170 feet + 107 feet = 5,277 feet
1 mile = 5,280 feet

Question 24.
The distance between Camp Birch and Camp Maple is __________ yards.
Answer:
The distance between Camp Birch and Camp Maple is 3 yards.
Explanation:
The distance from camp Birch to camp Maple is 9 feet.
1 yard = 3 feet
2 yards = 6 feet
3 yards = 9 feet

Question 25.
Camp __________ is nearer to the Bay Station than Camp Gum.
Answer:
Camp Plane is nearer to the Bay Station than Camp Gum.

Question 26.
The distance between Camp Plane and Camp Birch is slightly less than 1,760 ___________.
Answer:

Choose the unit that you would use to measure each. Write inch, foot, yard, or mile.

Question 27.
The length of a hiking trail ___________
Answer:
The length of a hiking trail in mile.

Question 28.
The length of an airplane ___________
Answer:
The length of an airplane in foot.

Question 29.
The height of a teacher ___________
Answer:
The height of a teacher in inch.

Follow More:

METROPOLIS Pivot Point Calculator

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 2 Practice 1 Using a Calculator to finish your assignments.

Math in Focus Grade 5 Chapter 2 Practice 1 Answer Key Using a Calculator

Add.

Question 1.
215 + 9,843 = ________
Answer: 10050
The addition is taking two or more numbers and adding them together, that is, it is the total sum of 2 or more numbers.
An addition sentence is a mathematical expression that shows two or more values added together and their sum.
215

The numbers that are added are called addends and the answer to addition is called the sum. In an addition sentence, the addends are added to get the sum. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.

Question 2.
6,789 + 18 = ____
Answer: 6807
Step 1: Write the numbers one below the other as per the places of the digits.
Step 2: Start adding from the ones digit. Write the sum under the ones digit. If the sum of the one’s digit is greater than 9, write the one’s digit of the sum under the ones and carry forward its tens digit to the tens column.
Step 3: Add the tens digits. (If there was a carry forward digit, add it along)

The numbers that are added are called addends and the answer to the addition is called the sum. In an addition sentence, the addends are added to get the sum. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.
6789 and 18 are the addends and the 6807 is a sum.

Question 3.
97 + 8,154 = ________
Answer: 8,251
Step 1: Write the numbers one below the other as per the places of the digits.
Step 2: Start adding from the ones digit. Write the sum under the ones digit. If the sum of the one’s digit is greater than 9, write the one’s digit of the sum under the ones and carry forward its tens digit to the tens column.
Step 3: Add the tens digits. (If there was a carry forward digit, add it along)

The numbers that are added are called addends and the answer to the addition is called the sum. In an addition sentence, the addends are added to get the sum. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.
8154 and 97 are the addends and the 8251 is a sum.

Question 4.
1,693 + 8,157 = ____
Answer: 9850
Step 1: Write the numbers one below the other as per the places of the digits.
Step 2: Start adding from the ones digit. Write the sum under the ones digit. If the sum of the one’s digit is greater than 9, write the one’s digit of the sum under the ones and carry forward its tens digit to the tens column.
Step 3: Add the tens digits. (If there was a carry forward digit, add it along)

The numbers that are added are called addends and the answer to the addition is called the sum. In an addition sentence, the addends are added to get the sum. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.
1693 and 8157 are the addends and 9850 is a sum.

Subtract.

Question 5.
8,215 – 79 = ___
Answer: 8,136
Subtraction means reducing a value from another value to get the required value.
The number 8,125 is called minuend.
The number 79 is called subtrahend.
The number 8,136 is called the difference.
8,125-79=8,136
The number you take away from is called the minuend. It is the biggest number in the equation.

Question 6.
6,286 – 129 = ____
Answer: 6157
Subtraction means reducing a value from another value to get the required value.
The number 6,286 is called minuend.
The number 129 is called subtrahend.
The number 6,157 is called the difference.
6286-129=6157
The number you take away from is called the minuend. It is the biggest number in the equation.

we need to borrow 1 to group 6 as 16 and then subtract 9 from it. Then we get 7.

Question 7.
2,159 – 1,998 = ____
Answer: 161
Subtraction means reducing a value from another value to get the required value.
The number 2,159 is called minuend.
The number 1,998 is called subtrahend.
The number 161 is called the difference.
2159-1998=161
The number you take away from is called the minuend. It is the biggest number in the equation.

We need to borrow 1 to group 1 as 11 and 5 as 15 and then subtract from it.

Question 8.
26,145 – 9,354 = ____
Answer: 16791
Subtraction means reducing a value from another value to get the required value.
The number 26,145 is called minuend.
The number 9354 is called subtrahend.
The number 16,791 is called the difference.
26,145-9,354=16,791
The number you take away from is called the minuend. It is the biggest number in the equation.

We need to borrow 1 to group 4 as 14, 1 as 11, 6 as 16 and then subtract from it.

Multiply.

Question 9.
359 × 12 = ___
Answer: 4308
In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life. The major application we can see in multiplication tables.
The multiplication of numbers say, ‘a’ and ‘b’, is stated as ‘a’ multiplied by ‘b’.
Multiplication symbol: The symbol of multiplication is denoted by a cross sign (×) and also sometimes by a dot (.).
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
1. The multiplicand is the total number of objects in each group
2. The multiplier is the number of equal groups
3. Product is the result of multiplication of multiplier and multiplicand.
Rules of multiplication (how to multiply):
There are various rules to multiply numbers. They are:
1. Multiplication of two integers is an integer.
2. Any number multiplied by 0 is 0.
3. Any number multiplied by 1 is equal to the original number.
4. If an integer is multiplied by multiples of 10, then the same number of 0s are added at the end of the original number. Example: 4 × 1000 = 4000.
5. The order of the numbers, does not matter, when multiplied together. Example: 2 × 3 × 4 × 5 = 5 × 4 × 3 × 2 = 3 × 2 × 4 × 5 = 120.
Now by applying all the rules we need to calculate 359×12:

Now I multiplied 2 with 9 then I get 18 I cancelled 8 and wrote in the problem and the remaining 1 will be added to the next means I multiplied 2 with 5 then I get 10. To this 10 I added the remaining 1 to the 10 then it becomes 11 again I cancelled 1 and wrote in the problem and so on…

Question 10.
217 × 58 = ___
Answer:12,586.
Multiplication symbol: The symbol of multiplication is denoted by a cross sign (×) and also sometimes by a dot (.).
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
1. The multiplicand is the total number of objects in each group
2. The multiplier is the number of equal groups
3. Product is the result of multiplication of multiplier and multiplicand.

Therefore, the answer is 12,586.

Question 11.
1,975 × 5 = ___
Answer: 9875
Multiplication symbol: The symbol of multiplication is denoted by a cross sign (×) and also sometimes by a dot (.).
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
1. The multiplicand is the total number of objects in each group
2. The multiplier is the number of equal groups
3. Product is the result of multiplication of multiplier and multiplicand.

We need to add the remaining numbers to the next multiple products.

Question 12.
7,050 × 8 = ___
Answer: 56400
Multiplication symbol: The symbol of multiplication is denoted by a cross sign (×) and also sometimes by a dot (.).
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
1. The multiplicand is the total number of objects in each group
2. The multiplier is the number of equal groups
3. Product is the result of multiplication of multiplier and multiplicand.

Multiplying with something with 0 will get 0. And I multiplied 8 by 5 I get 40. In 40 I cancelled 0 and the remaining 4 will be added to the next multiple products and so on… the process continues until the calculation completes.

Divide

Question 13.
504 ÷ 9 = ____
Answer: 56
Division: The meaning of divide is to separate into two or more equal parts, areas, classes, categories, groups or divisions. In simple words, the meaning of divide is to distribute the whole thing to a group in equal parts or make equal parts. Suppose, a diagonal of a square divides it into two triangles of equal area. The result of a division operation may or may not be an integer. Sometimes, the result will be in the form of decimal numbers.
Divide symbol: The symbol used to represent divide or division is ÷, slash (/) or a horizontal line ( _ ). These symbols are used as per convenience while dealing with various types of problems and calculations. Also, x/y or can be read as “x by y” or “x over y”.
Division Math Formula: The four important terms used in the division operation are dividend, divisor, quotient and remainder. The formula to calculate the division of two numbers is:
Dividend ÷ Divisor = Quotient + Remainder.
Here,
1. The dividend is the number, which is being divided
2. The divisor is the number, which divides the number (dividend) into equal parts
3. The quotient is the result of the division operation
4. The remainder is the leftover number in the division operation.
Points to Remember:
– If a number is divided by 1, the answer should be the same as the dividend. For example, 56/1 is 56.
– If the dividend and divisor are the same, then the quotient is 1. For example, 10/10 is 1.
– If a dividend is divided by 0, then the answer is undefined. For example, 15/0 is undefined.
Now by remembering all the points we calculate the division problem:

Question 14.
4,104 ÷ 6 = ___
Answer: 684
Division Math Formula: The four important terms used in the division operation are dividend, divisor, quotient and remainder. The formula to calculate the division of two numbers is:
Dividend ÷ Divisor = Quotient + Remainder.

We need to divide 4104 with 6 then we get the quotient 684 and the remainder is 0.

Question 15.
8,160 ÷ 85 = ____
Answer: 96
Division Math Formula: The four important terms used in the division operation are dividend, divisor, quotient and remainder. The formula to calculate the division of two numbers is:
Dividend ÷ Divisor = Quotient + Remainder.

96 is the quotient and 0 is the remainder.
Multiply 85 by 9 then we get 765. from 816 subtract 765 then we get 51 and in the dividend, we have 0. That 0 will get down. Then it will become 510. Again multiply 85 by 6. Then we get 510. Subtract 510 from the 510. Then it becomes 0 which is the remainder.

Question 16.
17,604 ÷ 18 = ____
Answer: 978
Division Math Formula: The four important terms used in the division operation are dividend, divisor, quotient and remainder. The formula to calculate the division of two numbers is:
Dividend ÷ Divisor = Quotient + Remainder.

In this problem also we have to multiply 18 by 9 then we get 162 and then subtract then we get 14. Now the tens place will get down then 14 becomes 140 and again multiply 18 by 7 then we get 126 again subtract 126 from 140 then we get 14 and again get down ones place 4, then 14 becomes 144. Subtract both we get 0 which is the remainder.

Only one path after each problem has the correct answer.
Trace Flavio’s path by choosing the paths with the correct answers.

Question 17.

The prize at the end of Flavio’s path is:
Answer: Football.
Flavio’s path is represented in the below diagram with the colouring:

Check For More:

IEX Pivot Point Calculator