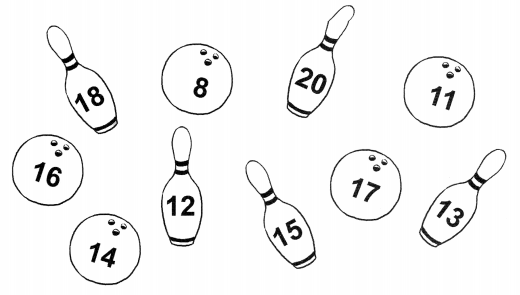
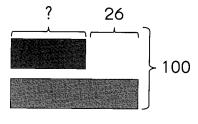
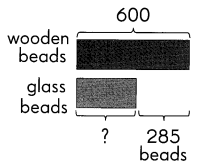
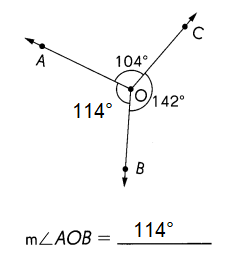
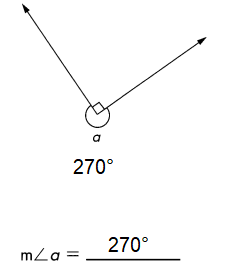
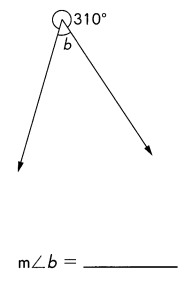
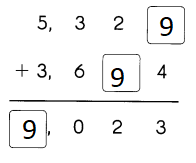Hillary – Page 61 – Math in Focus Answer Key

Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight

September 5, 2024September 4, 2024 by Hillary

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 15 Practice 2 Measuring Weight provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight

Ms. Meyer bought some meat, fruit, and vegetables for her Thanksgiving party.

Read the scales and write the weights.

Question 1.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 1$
The mushrooms weigh about ___________ ounces.
Answer:
The mushrooms weigh about 15 ounces.
Explanation:
In the above image we can observe the pointer is in between 14oz and 16oz. The mushrooms weigh about 15 ounces.

Question 2.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 2$
A slice of bread is about 1 ounce.
The cranberries weigh about ___________ ounces.
Answer:
The cranberries weigh about 6 ounces.
Explanation:
A slice of bread is about 1 ounce. In the above image we can observe 6 slices of bread in left side and cranberries in right side weighing balance. So the cranberries weigh about 6 ounces.

Question 3.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 3$
The leg of lamb weighs about___________ pounds.
Answer:
The leg of lamb weighs about 5.5 pounds.
Explanation:
In the above image we can observe the pointer is in between 4lb and 6lb. So, the leg of lamb weighs about 5.5 pounds.

Question 4.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 4$
The turkey weighs about ___________ pounds.
Answer:
The turkey weighs about 12 pounds.
Explanation:
In the above image we can observe 12lb’s in left side and turkey in right side weighing balance. We know that 1lb is equal to 1 pound. The turkey weighs about 12 pounds.

Question 5.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 5$
A loaf of bread is about 1 pound. The tomatoes weigh about ___________ pounds.
Answer:
The tomatoes weigh about 2 pounds.
Explanation:
In the above image we can observe 2 loaf of bread in left side and tomatoes in right side weighing balance. A loaf of bread is about 1 pound. So, the tomatoes weigh about 2 pounds.

Question 6.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 6$
The box of cereal weighs about ___________ ounces.
Answer:
The box of cereal weighs about 20 ounces.
Explanation:
In the above image we can observe 20oz’s in right side and cereal in right side weighing balance. We know that 1oz is equal to 1 ounce. The box of cereal weighs about 20 ounces.

Question 7.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 7$
The pumpkin weighs about __________ pounds.
Answer:
The pumpkin weighs about 8 pounds.
Explanation:
In the above image we can observe 10lb’s in left side weighing balance. The pumpkin and 2lb’s in right side weighing balance. The pumpkin weighs about 8 pounds.

Choose the unit that you would use to measure each. Write ounces, pounds, or tons.

Question 8.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 8$
A cement truck weighs about 5 __________.
Answer:
A cement truck weighs about 5 tons.

Question 9.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 9$
A package of butter weighs about 16 ___________.
Answer:
A package of butter weighs about 16 pounds.

Question 10.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 10$
A bowling ball weighs about 9 ___________.
Answer:
A bowling ball weighs about 9 pounds.

Question 11.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 11$
A mushroom weighs about 1 ___________.
Answer:
A mushroom weighs about 1 pound.

Question 12.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 12$
A carton of milk weighs about 12 ___________.
Answer:
A carton of milk weighs about 12 ounces.

Question 13.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 13$
A pile of magazines weighs about 5 ___________.
Answer:
A pile of magazines weighs about 5 pounds.

Question 14.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 14$
An elephant weighs about 3 __________.
Answer:
An elephant weighs about 3 tons.

Question 15.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 15$
Three granola bars weigh about 8 __________.
Answer:
Three granola bars weigh about 8 pounds.

Make a guess. Decide which animals weigh more than 1 ton, and which weigh less than 1 ton. Check your answers using the Internet or an encyclopedia.

$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 16$

Question 16.
$Math in Focus Grade 3 Chapter 15 Practice 2 Answer Key Measuring Weight 17$
Answer:
$Math-in-Focus-Grade-3-Chapter-15-Practice-2-Answer-Key-Measuring-Weight-17$

Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers

September 5, 2024September 4, 2024 by Hillary

This handy Math in Focus Grade 1 Workbook Answer Key Chapter 7 Practice 4 Making Patterns and Ordering Numbers detailed solutions for the textbook questions.

Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers

Solve.

Question 1.
Alex uses circles to make a pattern. How many circles come next in the pattern? Draw the circles in the empty box. Write the number of circles below this box.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 1$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_1$

Complete the patterns.

Question 2.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 2$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_2$

Question 3.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 3$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_3$

Look at the numbers. Fill in the blanks.

$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 14$

Question 4.
________ is 2 more than 15.
Answer: 17 is 2 more than 15.

Question 5.
________ is 2 less than 20.
Answer: 18 is 2 less than 20.

Question 6.
1 more than 18 is ___.
Answer: 1 more than 18 is 19.

Question 7.
2 less than 19 is ____.
Answer: 2 less than 19 is 17

Complete the number patterns.

Question 8.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 4$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_8$

Question 9.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 5$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_9$

Question 10.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 6$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_10$

Question 11.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 7$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_11$

Question 12.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 8$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_12$

Help Rosa order the bowling pins and balls.

$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 9$

Question 13.
Write the numbers on the $Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 10$ in order from greatest to least.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 11$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_13$

Question 14.
Write the numbers on the $Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 12$ in order from greatest to least.
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers 13$
Answer:
$Math in Focus Grade 1 Chapter 7 Practice 4 Answer Key Making Patterns and Ordering Numbers_14$

Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers

September 5, 2024September 4, 2024 by Hillary

This handy Math in Focus Grade 1 Workbook Answer Key Chapter 6 Practice 1 Ordinal Numbers detailed solutions for the textbook questions.

Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers

Circle.

Example

the 2nd corn
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 1$

Question 1.
the 5th princess
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 2$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-2$

Question 2.
the 8th bird
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 3$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-3$

Question 3.
the 7th duckling
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 4$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-4$

Color.

Question 4.
3 frogs
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 5$
the 3rd frog
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 6$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-6$

Question 5.
10 ants
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 7$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-7$

Match.

Question 6.
$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 8$
Answer:
$Math-in-Focus-Grade-1-Chapter-6-Practice-1-Answer-Key-Ordinal-Numbers-8$

Look at the picture. Answer the questions.

$Math in Focus Grade 1 Chapter 6 Practice 1 Answer Key Ordinal Numbers 9$

Question 7.
Who is first in the race?
Answer: Dora is first in the race.

Question 8.
Who is fourth in the race?____
Answer: Wanda is fourth in the race.

Question 9.
In which position is Tandi? ____
Answer: Tandi is in 6th position

Question 10.
In which position is Jenn?____
Answer: Jenn is in 5th position.

Question 11.
Who is last? ____
Answer: Meg is in last position in the race.

Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units

September 5, 2024September 4, 2024 by Hillary

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 9 Practice 5 Finding Length in Units to score better marks in the exam.

Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units

Count.

Fill in the blanks.

Example

$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 1$

Question 1.
$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 2$
The book is about ____ units long.
Answer: The book is about 6 units long.

Question 2.
$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 3$
The bat is about ___ units long.
Answer: The bat is about 9 units long.

Look at the picture. Fill in the blanks.

$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 4$

Question 3.
Footprint A is 4 units long.

Question 4.
Footprint B is ________ units long.
Answer: Footprint B is 3 units long.

Question 5.
Footprint C is ________ units long.
Answer: Footprint C is 5 units long.

Question 6.
Footprint D is ________ units long.
Answer: Footprint D is 6 units long.

Question 7.
Footprint ____ is the longest.
Answer: Footprint D is the longest.

Question 8.
Footprint ___ is shorter than Footprint A.
Answer: Footprint B is shorter than Footprint A.

Look at the picture. Fill in the blanks.

$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 5$

Question 9.
Strip ____ is the longest.
It is ____ units long.
This is ____ ten and ones.
Answer:
Strip C is the longest.
It is 15 units long.
This is 1 ten and ones.

Question 10.
Strip ____ is the shortest.
It is units ___ long.
Answer:
Strip D is the shortest.
It is units 4 long.

Question 11.
Strip ____ is as long as Strip ___
Answer: Strip A is as long as Strip E

Question 12.
Strip ___ is shorter than Strip C but longer than Strip E.
It is _____ units long.
This is ___ ten and ___ one.
Answer:
Strip D is shorter than Strip C but longer than Strip E.
It is 11 units long.
This is 1 ten and 1 one.

Look at the picture.
Fill in the blanks. Use numbers or the words in the box.

$Math in Focus Grade 1 Chapter 9 Practice 5 Answer Key Finding Length in Units 6$

Question 13.
The table is ________________ units long.
Answer: The table is 7 units long.

Question 14.
The bookshelf ¡s _________________ units tall.
Answer: The bookshelf ¡s 11 units tall.

Question 15.
Look at the stool the table, and the bookshelf. The bookshelf is the ____ thing. The stool is ___ than the table.
Answer: The bookshelf is the tallest thing. The stool is shorter than the table.

Question 16.
The vase is the ___ thing in the room.
Answer: The vase is the shortest thing in the room.

Question 17.
The string from the light is ___ than the pole of the fan.
Answer: The string from the light is longer than the pole of the fan.

Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units

September 5, 2024September 4, 2024 by Hillary

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 10 Practice 3 Finding Weight in Units to score better marks in the exam.

Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units

Fill in the blanks.

Example
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 1$
The weight of the gift is 11 units.

Question 1.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 2$
The weight of the lemon is ____ units.
Answer: The weight of the baby carrot is 13 units.

Question 2.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 3$
The weight of the gift is ____ units.
Answer: The weight of the gift is 15 units.

Question 3.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 4$
The weight of the lemon is ____ units.
Answer: The weight of the lemon is 9 units.

Question 4.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 5$
The weight of the egg is ____ units.
Answer: The weight of the egg is 15 units.

Question 5.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 6$
The weight of the egg is ___ units.
Answer: The weight of the egg is 10 units.

Fill in the blanks.

$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 7$

Question 6.
The weight of the toothbrush is ____ unit.
Answer: The weight of the toothbrush is 1 unit.

Question 7.
The weight of the soap is ___ units.
Answer: The weight of the soap is 10 units.

Question 8.
The weight of the toothpaste is ___ units.
Answer: The weight of the toothpaste is 5 units.

Question 9.
The ___ is lighter than the toothpaste.
Answer: The toothbrush is lighter than the toothpaste.

Question 10.
The soap is heavier than the ___.
Answer: The soap is heavier than the toothpaste and toothbrush

Question 11.
The ____ is the heaviest.
Answer: The soap is the heaviest.

Question 12.
The ___ is the lightest.
Answer: The toothbrush is the lightest.

Fill in the blanks.

$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 8$

Question 13.
The weight of Box A is ____ units.
Answer: The weight of Box A is 9 units.

Question 14.
The weight of Box B is ___ units.
Answer: The weight of Box B is 7 units.

Question 15.
The weight of Box C is ___ units.
Answer: The weight of Box C is 10units.

Question 16.
The weight of Box D is ___ units.
Answer: The weight of Box D is 6 units.

Question 17.
Box ___ is the heaviest.
Answer: Box C is the heaviest.

Question 18.
Box ___ is the lightest.
Answer: Box D is the lightest.

Question 19.
Box ___ is heavier than Box D.
Answer: Box B is heavier than Box D.

Question 20.
Box ___ is lighter than Box A.
Answer: Box B is lighter than Box A.

Question 21.
Arrange the Boxes A to D in order from the heaviest to the lightest.
$Math in Focus Grade 1 Chapter 10 Practice 3 Answer Key Finding Weight in Units 9$
Answer:
$Math-in-Focus-Grade-1-Chapter-10-Practice-3-Answer-Key-Finding-Weight-in-Units-9$

Math in Focus Grade 3 Mid Year Review Answer Key

September 5, 2024September 4, 2024 by Hillary

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Mid Year Review to score better marks in the exam.

Math in Focus Grade 3 Mid Year Review Answer Key

Mid-Year Review

Test Prep Multiple Choice

Fill in the circle next to the correct answer.

Question 1.
In the number 6,592, the digit 5 is in the ___ place. (Lesson 1.2)
(A) ones
(B) hundreds
(C) tens
(D) thousands
Answer: B
Explanation:
5 is in hundreds place
Each of these numerals has a different place value.
From left to right they are: thousands, hundreds, tens and ones.

Question 2.
Which number is 1,000 more than 1,629? (Lesson 1.3)
(A) 629
(B) 1,619
(C) 1,729
(D) 2,629
Answer: D
Explanation:
1000 + 1629 = 2629
Each of these numerals has a different place value.
From left to right they are: thousands, hundreds, tens and ones.

Question 3.
Estimate the sum of 342 and 525. Use front-end estimation. (Lesson 2.5)
(A) 300 + 500 = 800
(B) 300 + 530 = 830
(C) 340 + 500 = 840
(D) 340 + 530 = 870
Answer: A
Explanation:
300 + 500 = 800
Front-end estimation is a particular way of rounding numbers to estimate sums and differences. To use front- end estimation, add or subtract only the numbers in the greatest place value.

Question 4.
Estimate the difference between 828 and 535. Use rounding to the nearest hundred. (Lesson 2.4)
(A) 900 – 500 = 400
(B) 800 – 500 = 300
(C) 900 – 600 = 300
(D) 800 – 600 = 200
Answer: B
Explanation:
the difference between 828 and 535.
800 – 500 = 300
By rounding to the nearest hundred

Question 5.
0 × 9 = ____ (Lesson 6.1)
(A) 0
(B) 9
(C) 90
(D) 900
Answer: A
Explanation:
If a number is multiplied with 0 the product will be 0

Question 6.
To find the answer to 38 + 48, You can add 50 to ____ (Lesson 2.1)
(A) 38, then add 2
(B) 38, then subtract 2
(C) 48, then add 2
(D) 48, then subtract 2
Answer: B
Explanation:
To find the answer to 38 + 48, You can add 50 to 38 and subtract 2
38 + 50 – 2 = 86

Question 7.
What is the missing digit? (Lesson 3.3)
$Math in Focus Grade 3 Mid Year Review Answer Key 1$
(A) 1
(B) 2
(C) 5
(D) 9
Answer: D

Explanation:
5329 + 3694 = 9023
The missing digit is 9

Question 8.
There are four numbers on a whiteboard:
1,390, 1,125, 1,580, and 1,625.
The difference between two of the numbers is 235. What are the two numbers? (Lesson 4.3)
(A) 1,580 and 1,390
(B) 1,625 and 1,390
(C) 1,390 and 1,125
(D) 1,580 and 1,125
Answer: B
Explanation:
the two numbers are 1,625 and 1,390
1,625 and 1,390 = 235

Question 9.
How many numbers between 31 and 50 can be divided by 6 with no remainder? (Lesson 8.4)
(A) 1
(B) 2
(C) 3
(D) 4
Answer: C
Explanation:
the numbers between 31 and 50 = 18
18 ÷ 6 = 3

Question 10.
Add 4,786 and 1,078. (Lesson 3.3)
(A) 3,708
(B) 3,808
(C) 5,764
(D) 5,864
Answer: D
Explanation:
4,786 and 1,078. = 5864

Question 11.
Subtract 1,786 from 3,000. (Lesson 4.3)
(A) 1,204
(B) 1,214
(C) 2,786
(D) 4,786
Answer: B
Explanation:
The difference between 3000 – 1786 = 1214

Question 12.
215 × 4 = ___ (Lesson 7.3)
(A) 172
(B) 211
(C) 219
(D) 860
Answer: D
Explanation:
215 × 4 = 860
The product of 215 and 4 = 860

Question 13.
Which of the following is the same as 5 × 9? (Lesson 6.5)
(A) 9 + 5
(B) 5 + 5 + 9 + 9
(C) 5 + 5 + 5 + 5 + 5
(D) 9 + 9 + 9 + 9 + 9
Answer: D
Explanation:
5 x 9 = 9 + 9 + 9 + 9 + 9 = 45
5 x 9 = 9 + 9 + 9 + 9 + 9 are same.

Question 14.
Drew has 87 pebbles. He divides the pebbles equally into 3 bags. How many pebbles does he have in each bag? (Lesson 8.5)
(A) 29
(B) 84
(C) 90
(D) 261
Answer: A
Explanation:
Drew has 87 pebbles. He divides the pebbles equally into 3 bags.
87 ÷ 3 = 29
29 pebbles that he have in each bag

Question 15.
The sum of two numbers is 100. The difference between the two numbers is 26. What is the number that is less? (Lesson 5.1)
$Math in Focus Grade 3 Mid Year Review Answer Key 3$
(A) 13
(B) 24
(C) 37
(D) 63
Answer: B
Explanation:
The sum of two numbers is 100
The difference between the two numbers is 26.
50 + 50 = 100
50 – 26 = 24

Short Answer
Read the questions carefully.
Write each answer in the space provided.

Question 16.
Write three thousand, fourteen in standard form. (Lesson 1.1)
_________
Answer:
3014
Explanation:
three thousand, fourteen in standard form is 3014

Question 17.
What is the value of the digit 5 in the number 5,631? (Lesson 1.2)
_________
Answer:
Thousand is the value of the digit 5 in the number 5,631
Explanation:
Each of these numerals has a different place value.
From left to right they are: thousands, hundreds, tens and ones.

Question 18.
Use the digits below to make three 3-digit odd numbers and three 3-digit even numbers. Do not repeat the same digits in a number. (Lesson 8.3)
$Math in Focus Grade 3 Mid Year Review Answer Key 4$
Answer:

Explanation:
three 3-digit odd numbers = 139
and three 3-digit even numbers = 824
The numbers are not repeated

Question 19.
Add 1,850 + 59. (Lesson 3.2)
_________
Answer:
1909
Explanation:
The sum of 1850 + 59 = 1909

Question 20.
70 × 4 = ? (Lesson 17.1)
_________
Answer:
280
Explanation:
70 × 4 = 280
The product of 70 and 4 = 280

Question 21.
In 59 ÷ 2, the quotient is ___, and the remainder is ___ (Lesson 8.2)
Answer:
In 59 ÷ 2, the quotient is 29.5, and the remainder is 0
Explanation:

Question 22.
Shaun takes 300 photographs at the zoo. Sheena takes twice as many photographs as Shaun. How many photographs do they take in all? (Lesson 9.1)
____ photos
Answer:
900 photos
Explanation:
Shaun takes 300 photographs at the zoo.
Sheena takes twice as many photographs as Shaun.
300 x 2 = 600
600 + 300 = 900
900 photographs that they take in all

Question 23.
Shannon has 78 animal stickers. She has three times as many animal stickers as her brother, Ryan. How many animal stickers does Ryan have? (Lesson 9.3)
____ paperclips
Answer:
312 paperclips
Explanation:
Shannon has 78 animal stickers.
She has three times as many animal stickers as her brother, Ryan.
78 x 3 = 234
234 + 78 = 312
312 animal stickers that Ryan have

Question 24.
The sum of two numbers is 1,500. The difference between these two numbers is 300. Find these two numbers from the numbers provided. (Lessons 3.2 and 4.1)
1,200 600 300 700 800 900
__________
Answer:
900 + 600 = 1500
900 – 600 = 300
Explanation:
The sum of two numbers is 1,500.
The difference between these two numbers is 300.
two numbers from the numbers provided are 900 and 600

Question 25.
Caroline packs some glue sticks into 8 bags. She has 12 glue sticks left over. If there are 25 glue sticks in each bag, how many glue sticks did she have at first? (Lessons 7.3 and 3.1)
___________
Answer:
212 Glue sticks at first.
Explanation:
Caroline packs some glue sticks into 8 bags.
If there are 25 glue sticks in each bag,
25 x 8 = 200
total 200 bags
200 + 12 = 212 Glue sticks

Question 26.
What is the product of 1 × 7 × 2?
Use the number lines to help you. (Lessons 6.1 and 6.2)
1 × 7 × 2 = 1 × ____
= ______
$Math in Focus Grade 3 Mid Year Review Answer Key 5$
1 × 7 × 2 = ___ × 2
= ______
$Math in Focus Grade 3 Mid Year Review Answer Key 6$
So, 1 × ___ = ___ × 2
= _____
Answer:
So, 1 × 14 = 7 × 2
= 14
Explanation:
1 × 7 × 2 = 1 × 14
= 14

1 × 7 × 2 = 7 × 2
= 14

Question 27.
Find the sum of 938 and 8,163. (Lesson 3.3) 28. Find the difference between 6,215 and 8,356. (Lesson 4.3)
___________
Answer:
9101 , 2141
Explanation:
938 + 8,163 = 9101
the sum of 938 and 8,163 = 9101
6125 – 8356 = 2141
the difference between 6,215 and 8,356 = 2141

Question 29.
Find the product of 154 and 4. (Lesson 7.3)
_________
Answer:
616
Explanation:
The product of 154 and 4 is 616

Question 30.
Use the digits below to form two 2-digit numbers. Each number has a remainder of 1 when divided by 4. (Lesson 8.2)
1 3 7 9
__________
Answer:
17
Explanation:
The two digit number selected is 17
17 ÷ 4 = 4
and remainder = 1
4 x 4 = 16
17 – 16 = 1

Question 31.
Find the difference between 45 ÷ 5 and 5 × 7. (Lessons 4.3, 6.3, and 7.1)
___________
Answer:
26
Explanation:
45 ÷ 5 = 9
5 × 7 = 35
The difference between 45 ÷ 5 and 5 × 7
35 – 9 = 26

Question 32.
Use the model. How many stamps does Alex have? (Lesson 5.1)
$Math in Focus Grade 3 Mid Year Review Answer Key 7$
_____ stamps
Answer:
29 + 21 = 50
29 stamps
Explanation:
Alex and Jim has 100 stamps in all
Jim has 50 stamps
As the stamps are divided equally among Jim and Alex
both have 50 and 50
50 – 21 = 29

Question 33.
A craft store sells 1,1 24 fewer pieces of red art paper than blue art paper. It sells 2,317 pieces of red art paper. How many pieces of red and blue art paper does the craft store sell? (Lessons 3.3 and 4.3)
_____ pieces
Answer:
3510 pieces
Explanation:
A craft store sells 1,1 24 fewer pieces of red art paper than blue art paper.
It sells 2,317 pieces of red art paper.
2317 – 1124 = 1193
2317 + 1193 = 3510
3510 pieces of red and blue art paper that the craft store sell

Question 34.
Ngu walks 250 feet. She walks 65 feet more than Pauline. How far does Pauline walk? (Lesson 4.3)
____ feet
Answer:
315 feet
Explanation:
Ngu walks 250 feet.
She walks 65 feet more than Pauline.
250 +65 = 315
315 feet far that Pauline walk

Question 35.
Oomi makes 4 necklaces. She uses 156 beads for each necklace. How many beads does she use in all? (Lesson 7.3)
____ beads
Answer:
624 beads
Explanation:
Oomi makes 4 necklaces. She uses 156 beads for each necklace.
156 x 4 = 624
624 beads that she use in all

Extended Response

Solve. Show your work.

Question 36.
Jolene has 600 wooden beads. She has 285 fewer glass beads than wooden beads.

a. How many glass beads does Jolene have?
$Math in Focus Grade 3 Mid Year Review Answer Key 8$
Answer:
315 glass beads
Explanation:
The total of wooden beads and glass beads = 600 + 600 = 1200
Jolene have 600 – 285 = 315
315 glass beads that Jolene have

b. How many wooden beads does she have if she uses 150 of them to make necklaces?
$Math in Focus Grade 3 Mid Year Review Answer Key 9$
Answer:
600 – 150 = 450
Explanation:
450 wooden beads that she have if she uses 150 of them to make necklaces

Question 37.
Company A gets 3,700 hits on their website. Company B gets 450 fewer hits than Company A.

a. How many hits does Company B get?
Answer:
3700 – 450 = 3250
3250 hits that Company B get

b. How many hits do both companies get in all?
Answer:
3700 + 3250 = 6950
6950 hits that both the companies get in all

Question 38.
Noah swims 80 laps in 5 days. He swims the same number of laps every day.

a. How many laps does he swim in a day?
Answer:
80 ÷ 5 = 16
16 laps that he swim in a day

b. How many laps does he swim in 4 days?
Answer:
16 x 4 = 64
64 laps that he swim in 4 days

Question 39.
Jose has 88 stickers. He puts 4 stickers on each bookmark. He gives all his bookmarks away to his friends. Each friend receives 2 bookmarks.

a. How many bookmarks does he put stickers on?
Answer:
Jose has 88 stickers. He puts 4 stickers on each bookmark.
88 ÷ 4 = 22
He gives all his bookmarks away to his friends. Each friend receives 2 bookmarks.
22 ÷ 2 = 11
22 bookmarks that he put stickers on

b. How many friends does he have?
Answer:
22 ÷ 2 = 11
11 friends that he have

Question 40.
A factory delivers 5 containers of pottery to a store. Each container has 1 62 pieces of pottery. The store owner discovers 24 pieces of pottery are broken. How many pieces of pottery are not broken?
Answer:
786 pieces
Explanation:
A factory delivers 5 containers of pottery to a store.
Each container has 1 62 pieces of pottery.
162 x 5 = 810
The store owner discovers 24 pieces of pottery are broken.
810 -24 = 786
786 pieces of pottery are not broken

Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000

September 4, 2024September 3, 2024 by Hillary

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 1 Practice 1 Numbers to 10,000,000 to finish your assignments.

Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000

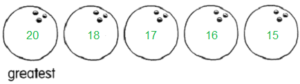
Count on or back by ten thousand or hundred thousand. Then fill in the blanks.

Question 1.
40,000 50,000 60,000 _____ ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The number 40,000:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q1.1$
The ten thousand place value for 40,000 is 4.
The number 50,000:
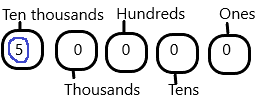
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q1.2$
The ten thousand place value for 50,000 is 5.
The number 60,000:
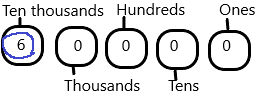
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q1.3$
The ten thousand place value for 60,000 is 6.

Question 2.
900,000 800,000 700,000 ___ _____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The number 900,000:
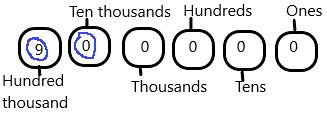
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q2$
The hundred thousand place value for 900,000 is 9
The ten thousand place value for 900,000 is 0.
The number 800,000:
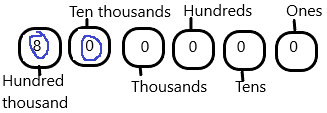
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q2.1$
The hundred thousand place value for 800,000 is 8
The ten thousand place value for 800,000 is 0.
The number 700,000:
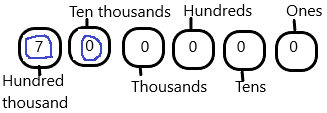
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q2.2$
The hundred thousand place value for 700,000 is 7.
The ten thousand place value for 700,000 is 0.

Complete the table. Then write the number in standard form and in word form.

Question 3.
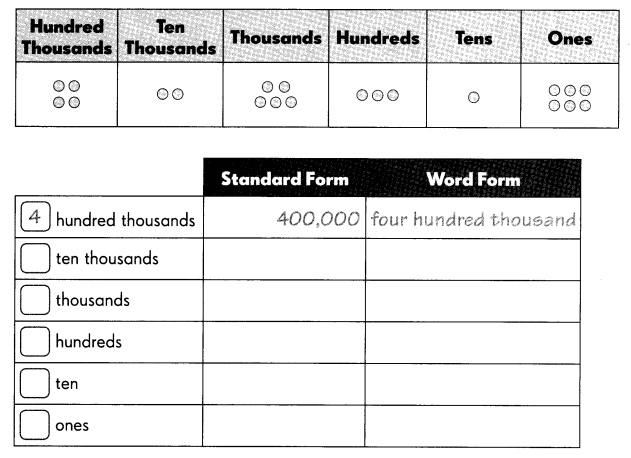
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 1$
Number in standard form: ______
Number in word form: ______
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
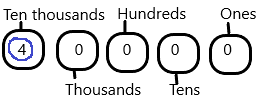
PLACE VALUE CHART:
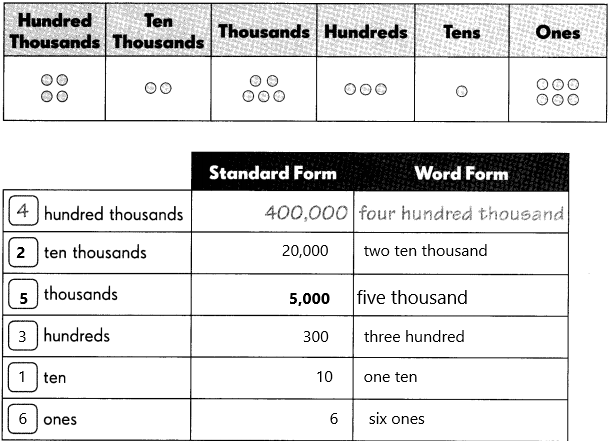
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q3$
Number in standard form: 425,316
Number in word form: four hundred twenty-five thousand, three hundred sixteen.

Write each number in standard form.

Question 4.
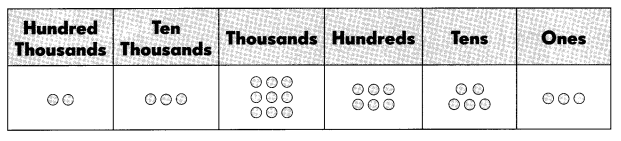
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 2$
The number is ____.
Answer: 239,653
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q4$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 2 hundred thousands+3 ten thousands+9 thousands+6 hundreds+5 tens+3 ones
The standard form is 239,653.

Question 5.
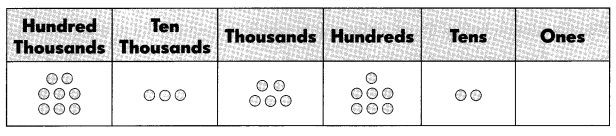
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 3$
The number is ____.
Answer: 835,720
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q5$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 8 hundred thousands+3 ten thousands+5 thousands+7 hundreds+2 tens+0 ones
The standard form is 835,720.

Question 6.
eight hundred sixteen thousand, nine hundred forty-three _____
First, read the thousands period: eight hundred sixteen thousand – 816,000 Then, read the remaining period: nine hundred forty-three — 943
Answer: 816,943
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q6$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 8 hundred thousands+1 ten thousands+6 thousands+9 hundreds+4 tens+3 ones
The standard form is 816,943.

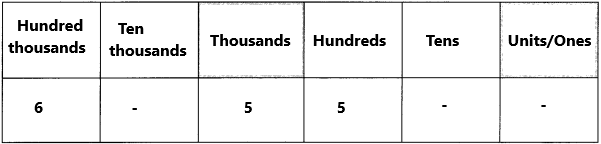
Question 7.
six hundred five thousand, five hundred ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q7$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 6 hundred thousands+0 ten thousands+5 thousands+5 hundreds+0 tens+0 ones
The standard form is 605,500.
First, read the thousands of period: 605,000. Then, read the remaining period: 500.

Question 8.
one hundred three thousand, thirty-one ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q8$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 1 hundred thousands+0 ten thousands+3 thousands+0 hundreds+3 tens+1 ones
The standard form is 103,031.

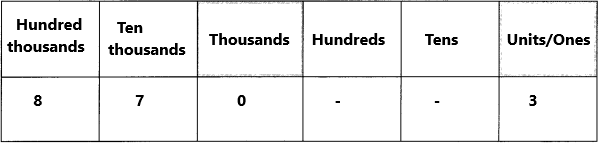
Question 9.
eight hundred seventy thousand, three ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q9$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 8 hundred thousands+7 ten thousands+0 thousands+0 hundreds+0 tens+3 ones
Write: 870,003.
Say: Eight hundred seventy thousand three.

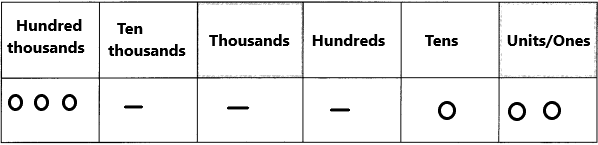
Question 10.
three hundred thousand, twelve ___
Answer: 300,012
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
PLACE VALUE CHART:
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q10$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 3 hundred thousands+0 ten thousands+0 thousands+0 hundreds+1 tens+2 ones
Write: 300,012
Say: Three hundred thousand twelve.

Fill in the headings. Write Tens, Hundreds, Ten Thousand, or Hundred Thousands. Then write each number in word form.

Question 11.
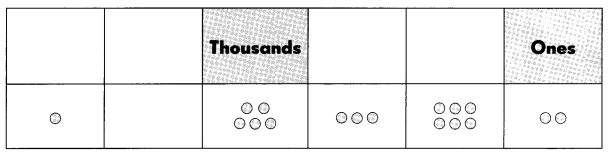
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 4$
The number is _____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q11$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 1 hundred thousands+0 ten thousands+5 thousands+3 hundreds+6 tens+2 ones
Write: 105,362.
Say One hundred five thousand, three hundred sixty-two.

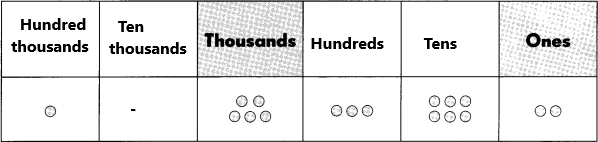
Question 12.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 5$
The number is _____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in the general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q12$
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
Think: 5 hundred thousands+6 ten thousands+0 thousands+0 hundreds+2 tens+1 ones
Write:560,021.
Say five hundred sixty thousand, twenty-one.

Write each number in word form.
65,000 — sixty-five thousand
142 — one hundred forty-two

Question 13.
65, 142 _____
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
The number 65,142 can be written in word form as:
sixty-five thousand, one hundred forty-two.
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q13$
The given number 65,142: o hundred thousand+6 ten thousand+5 thousand+1 hundred+4 tens+2 ones.
Write: 65,142
Say: Sixty-five thousand, one hundred forty two.

Question 14.
368,400 _____
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
The number 368,400 can be written in word form as:
Three hundred sixty-eight thousand, four hundred.
Zeros may stand for nothing, but that doesn’t mean you can leave them out. They keep other digits in the correct places.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q14$
The given number 368,400: 3 hundred thousand+6 ten thousand+8 thousand+4 hundred+0 tens+0 ones.
Write: 368,400
Say: Three hundred sixty-eight thousand, four hundred.

Complete to express each number in word form.

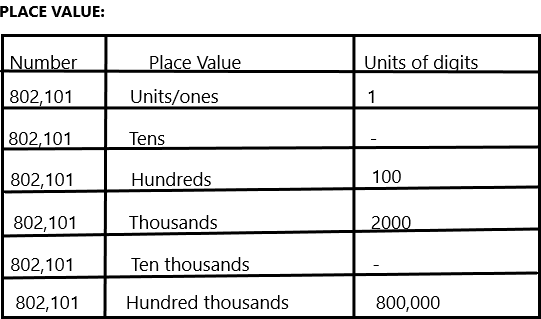
Question 15.
802,101 eight hundred two thousand, one hundred _________
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The given number is 802,101 and this can be written in word form as:
Eight hundred two thousand, one hundred one.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q15$

Question 16.
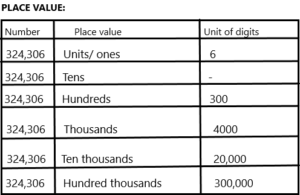
324,306 three hundred twenty-four ____, three hundred six
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The given number is 324,306 and this can be written in word form as:
Three hundred twenty-four thousand, three hundred six.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q16$

Question 17.
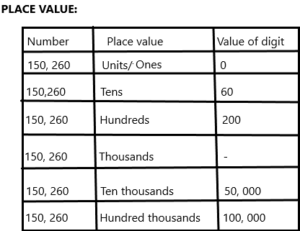
150,260 one hundred fifty thousand, ___ hundred sixty
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The given number is 150, 260 and this can be written in word form as:
One hundred fifty thousand, two hundred sixty.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q17$

Question 18.
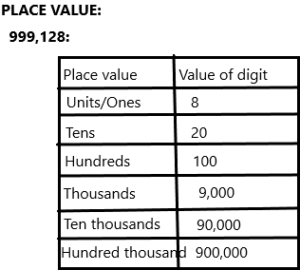
999,1 98 nine hundred ___ thousand, one hundred ______________
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.

Place value tells you how much each digit stands for
Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
A place-value chart tells you how many hundreds, tens, and ones to use.

The given number is 999,198 and this can be written in word form as:
Nine hundred ninety thousand, one hundred ninety-eight.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q20$

Use the table showing the populations of some cities to answer the questions.

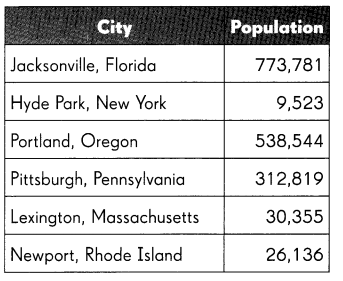
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 6$

Use the table showing the populations of some cities to answer the questions.

Question 19.
Write the population of Pittsburgh in word form.
Answer:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
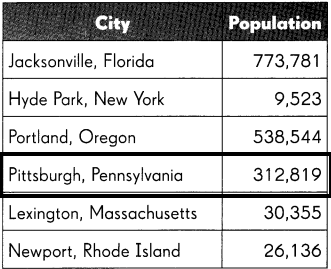
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000$
The population in Pittsburgh is 312,819.
In the word form, we can write as Three lakh twelve thousand eight hundred and nineteen.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q19$

Question 20.
Which city has the least population? What is its population?
Answer: Hyde Park, New York.
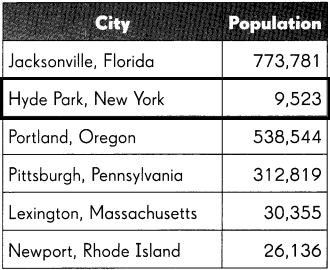
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q18$
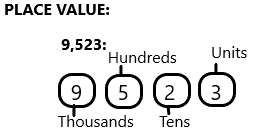
The least population of the city is Hyde Park, New York. And the population is 9,523.
The place value starts from thousands when compared to all the place values that’s why I choose New York which has the lowest population.
$Math in Focus Grade 5 Chapter 1 Practice 1 Answer Key Numbers to 10,000,000 q18.1$

Math in Focus Grade 5 Chapter 5 Practice 3 Answer Key Simplifying Algebraic Expressions

September 4, 2024September 3, 2024 by Hillary

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 5 Practice 3 Simplifying Algebraic Expressions to finish your assignments.

Math in Focus Grade 5 Chapter 5 Practice 3 Answer Key Simplifying Algebraic Expressions

Simplify each expression.

Example
c + c + c + c = 4c

Question 1.
6p + 3 p =
Answer:
6p + 3 p = 9p
Explanation:
The given expression is 6p + 3p. Add 6p with 3p the sum is 9p.

Question 2.
b + 3 b + 5b =
Answer:
b + 3b + 5b = 9b
Explanation:
The given expression is b + 3b + 5b. Add b with 3b and 5b the sum is 9b.

Question 3.
10k – 3k =
Answer:
10k – 3k = 7k
Explanation:
The given expression is 10k – 3k. Subtract 3k from 10k the difference is 7k.

Question 4.
12p – 12p =
Answer:
12p – 12p = 0
Explanation:
The given expression is 12p – 12p. Subtract 12p from 12p the difference is 0.

Question 5.
6p – 2p – 3p =
Answer:
6p – 2p – 3p = 6p – 5p = 1p
Explanation:
The given expression is 6p – 2p – 3p. First add 2p and 3p the sum is 5p. Subtract 5p from 6p the difference is 1p.

Question 6.
10a – a + 2a =
Answer:
10a – a + 2a = 9a + 2a = 11a
Explanation:
The given expression is 10a – a + 2a. First subtract a from 10a the difference is 9a. Now add 9a with 2a the sum is 11a.

Question 7.
4c + c – 5c =
Answer:
4c + c – 5c = 5c – 5c = 0
Explanation:
The given expression is 4c + c – 5c. First add 4c with c the sum is 5c. Subtract 5c from 5c the difference is 0.

Question 8.
10f – 4f + f =
Answer:
10f – 4f + f = 6f + f = 7f
Explanation:
The given expression is 10f – 4f + f. First subtract 4f from 10f the difference is 6f. Add 6f with f the sum is 7f.

Simplify each expression.

Example
5x + 2x + 4 = 7x + 4

Question 9.
x + 5x – 9 =
Answer:
x + 5x – 9 = 6x – 9
Explanation:
The given expression is x + 5x – 9. Add x with 5x the sum is 6x. The simplified expression is 6x – 9.

Question 10.
2m + 4 + 6m =
Answer:
2m + 4 + 6m = 8m + 4
Explanation:
The given expression is 2m + 4 + 6m. Add 2m with 6m the sum is 8m. The simplified expression is 8m + 4.

Question 11.
10p – 4p – 5 =
Answer:
10p – 4p – 5 = 6p – 5
Explanation:
The given expression is 10p – 4p – 5. Subtract 4p from 10p the difference is 6p. The simplified expression is 6p – 5.

Question 12.
4 + 5k – 4k =
Answer:
4 + 5k – 4k = 4 + k
Explanation:
The given expression is 4 + 5k – 4k . Subtract 4k from 5k the difference is k. The simplified expression is 4 + k.

Question 13.
2 + 6b – 1 + 4b =
Answer:
2 + 6b – 1 + 4b = 1 +10b
Explanation:
The given expression is 2 + 6b – 1 + 4b. Subtract 1 from 2 the difference is 1. Add 6b with 4b the sum is 10b. The simplified expression is 1 + 10b.

Question 14.
5c + 3 – 2c + 5 =
Answer:
5c + 3 – 2c + 5 = 3c + 8
Explanation:
The given expression is 5c + 3 – 2c + 5. Subtract 2c from 5c the difference is 3c. Add 3 with 5 the sum is 8. The simplified expression is 3c + 8.

Question 15.
9e – 2e + 3 + 5e =
Answer:
9e – 2e + 3 + 5e = 7e + 5e + 3 = 12e + 3
Explanation:
The given expression is 9e – 2e + 3 + 5e. Subtract 2e from 9e the difference is 7e. Add 7e with 5e the sum is 12e. The simplified expression is 12e + 3.

Question 16.
6h + 12 + 2h – 6 =
Answer:
6h + 12 + 2h – 6 = 8h + 6
Explanation:
The given expression is 6h + 12 + 2h – 6. Subtract 6 from 12 the difference is 6. Add 6h with 2h the sum is 8h. The simplified expression is 8h + 6.

Write an algebraic expression for each situation.

Question 17.
The length of a piece of fabric is 8y yards. London cuts 7 yards from it to make some cushion covers. He then cuts another 3y yards to make a curtain. The remaining material is cut into 4 equal pieces. How long is each piece?
Answer:
The length of a piece of fabric is 8y yards. London cuts 7 yards from it to make some cushion covers.
(8y – 7) yards
He then cuts another 3y yards to make a curtain.
(8y – 7 – 3y) yards
The remaining material is cut into 4 equal pieces.
(8y – 7 – 3y)/4 yards
(5y – 7)/4 yards

Question 18.
Ling has 4m pounds of flour. She buys another 2 packages of flour, each weighing m pounds. How much flour does Ling have now in terms of m?
Answer:
The algebraic expression is 4m + 2m = 6m.
Explanation:
Ling has 4m pounds of flour. She buys another 2 packages of flour, each weighing m pounds. The 2 packages of flour is represented as 2m. Add 4m with 2m the sum is 6m. Ling have 6m pounds of flour.

Question 19.
On Monday, Linus made 5k paper cranes and gave 2k paper cranes to his friends. On Tuesday, he made another 4k paper ‘ cranes. His friend gave him 5 paper cranes. How many paper cranes does he have now in terms of k?
Answer:
On Monday, Linus made 5k paper cranes and gave 2k paper cranes to his friends.
5k – 2k = 3k
On Tuesday, he made another 4k paper ‘ cranes. His friend gave him 5 paper cranes.
4k + 5k = 9k
3k + 9k = 12k
Now, he have 12k paper cranes.

Question 20.
At the market, a pear costs b cents and an apple costs 7 cents less than a pear. Randy buys 4 pears and an apple. How much does Randy pay in terms of b?
Answer:
The cost of pears is b cents.
The cost of an apple is 7 cents less than a pear = b – 7
Randy buys 4 pears and an apple.
4b + b – 7 = 5b – 7
At the market, Randy pays 5b -7.

Math in Focus Grade 5 Chapter 10 Answer Key Percent

September 4, 2024September 3, 2024 by Hillary

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 10 Percent to score better marks in the exam.

Math in Focus Grade 5 Chapter 10 Answer Key Percent

Math Journal

Arnold had dinner at a restaurant with his family. The dinner cost $72. In addition, he paid 7% meals tax on the dinner. How much did Arnold pay for the dinner?

Tyrone worked out the answer using his calculator like this:
93% × $72 = $66.96
Brandon worked out the answer using his calculator like this:
107% × $72 = $77.04
Whose answer is correct? Explain why his answer is correct.
Answer:
Brandon answer is correct
Explanation:
Arnold paid
7% of tax and 100% of his bill
107% × $72 = $77.04
or
Arnold paid
$72 + $7% = $72 + $5.04 = $77.04

Put on Your Thinking Cap!

Challenging Practice

Solve. Show your work.

Question 1.
Mr. Stanton bought a cell phone at 80% of the regular price. The regular price of the phone was $450. Mr. Wilson bought the same cell phone but paid $500 for it. How much more did Mr. Wilson pay than Mr. Stanton?
Answer:
140 more did Mr. Wilson pay than Mr. Stanton
Explanation:
Cell phone regular price is $450
Mr. Stanton paid 80% of 450 = $360
80% x $450= $360
Mr. Wilson paid $500
500 – 360 = 140
Mr. Wilson pay 140 more than Mr. Stanton.

Question 2.
Helen has 30 tickets. Gina has 20 more tickets than Helen. What percent of her tickets must Gina give Helen so that both of them have the same number of tickets?
Answer: 20%
Explanation:
Helen has 30 tickets.
Gina has 20 more tickets than Helen = 30 + 20 = 50 tickets
20 percent of her tickets must Gina give Helen so that both of them have the same number of tickets
such that both can have 40 tickets
Gina has 50 tickets
if she give 10 tickets to Helen ,now both are 40 tickets
20% of 50 is 10

Put on Your Thinking cap!

Problem Solving

Solve. Show your work.

Michelle collects U.S., Canadian, and Mexican stamps. In her collection, 80% of the stamps are U.S. and Mexican stamps. There are 3 times as many U.S. stamps as Mexican stamps. What percent of Michelle’s collection is made up of U.S. stamps?
Answer:
53.4%
Explanation:
100% of U.S. stamps + Canadian stamps + Mexican stamps
80% of the stamps are U.S. stamps + Mexican stamps
20% Canadian stamps
let Mexican stamp is x then
U.S stamps 3x
What percent of Michelle’s collection is made up of U.S. stamps?
80% —– 3X
? —– X
26.6 % Mexican
80% – 26.6% = 53.4%

Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point

September 4, 2024September 3, 2024 by Hillary

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 12 Practice 2 Angles at a Point provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point

In each figure, the rays meet at a point. Use a protractor to find unknown angle measures.

Question 1.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 1$
m∠a = ___
m∠b = ___
m∠c = ____
m∠a + m∠b + m∠c = ___ + ___ + ___
= ____
Answer:
m∠a = 120°
m∠b = 90°
m∠c = 150°
m∠a + m∠b + m∠c = 120° + 90° + 150° = 360°
Explanation:
Angle less than 180° is obtuse angle.
m∠a = 120°
m∠c = 150°
Angle 90° is Right angle triangle.
m∠b = 90°
Add all the angles to get a complete angle.
m∠a + m∠b + m∠c = 120° + 90° + 150° = 360°

Question 2.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 2$
m∠AOB = ___
m∠BOC = ___
m∠COD = ____
m∠DOE = _____
m∠AOE = ____
m∠AOB + m∠BOC + m∠COD + m∠DOE + m∠AOE
= ___ + ___ + ___ + ___ + ____
= ____
Answer:
m∠AOB = 140°
m∠BOC = 40°
m∠COD = 50°
m∠DOE = 100°
m∠AOE = 30°
m∠AOB + m∠BOC + m∠COD + m∠DOE + m∠AOE
= 140°+40°+50°+100°+30°= 360° is called a complete angle.
Explanation:

m∠AOB = 140°
m∠DOE = 100°
Angle less than 180° is obtuse angle.
m∠BOC = 40°
m∠COD = 50°
m∠AOE = 30°
Angle 90° is Right angle triangle.
Add all the angles to show complete angle.
m∠AOB + m∠BOC + m∠COD + m∠DOE + m∠AOE
= 140°+40°+50°+100°+30°= 360°

Name the angles at a point.

Question 3.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 3$
Answer:
∠a = 120°
∠b= 80°
∠c = 160°
∠a + ∠b + ∠c = 120° + 80° + 160° = 360°
Explanation:
∠a = 120° and ∠c = 160° are obtuse angles.
∠b = 80° is acute angle.
∠a + ∠b + ∠c = 120° + 80° + 160° = 360°

Question 4.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 4$
Answer:
m∠XOW = 40°
m∠ZOW = 90°
m∠ZOY = 140°
m∠XOY=90°
m∠XOY + m∠XOW + m∠ZOW + m∠ZOY + m∠XOY
= 40° + 90° + 140° + 90° = 360°
Explanation:

In the above picture
m∠ZOW = 90° and m∠XOY=90° are right angles.
m∠XOW = 40° is acute angle as the angle is less than 90°
m∠ZOY = 140° is obtuse angle as the angle is less than 180°
Add all the angles to get complete angle.
m∠XOY + m∠XOW + m∠ZOW + m∠ZOY + m∠XOY
= 40° + 90° + 140° + 90° = 360°

Question 5.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 5$
Answer:
∠a = 60°
∠b= 120°
∠c = 60°
∠d= 120°
∠a + ∠b + ∠c +∠d = 60°+ 120° + 60° + 120° = 360°
Explanation:

As shown in the above picture
∠a + ∠c= 60° are acute angles as the angle is less than 90°
∠b and ∠d = 120° are obtuse angles as the angle is less than 180°
Add all the angles to get complete angle.
∠a + ∠b + ∠c +∠d = 60°+ 120° + 60° + 120° = 360°

Question 6.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 6$
Answer:
∠e = 90°
∠f = 90°
∠g = 30°
∠h = 100°
∠k = 50°
∠e + ∠f + ∠g +∠h + ∠k = 90° + 90°+ 30° + 100° + 50° = 360°
Explanation:

As shown in the above picture
∠g = 30° and ∠k= 50° are acute angles as the angle is less than 90°
∠e = 90° and ∠f= 90° are right angles as the angle is 90°
∠h = 100° is obtuse angle as the angle is less than 180°
Add all the angles to get complete angle.
∠e + ∠f + ∠g +∠h + ∠k = 90° + 90°+ 30° + 100° + 50° = 360°

Find the unknown angle measures.

Question 7.
Find the measure of ∠AOB.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 7$
Answer: 114°
Explanation:
complete angle is 360°
∠AOC +∠COB = 104° + 142° = 246°
∠AOB = 360° – 246° = 114°

Question 8.
Find the measure of ∠a.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 8$
Answer: 270°
Explanation:
complete angle is 360°
360°- 90° = 270°

Question 9.
Find the measure of ∠b.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 9$
Answer: 50°
Explanation:
complete angle is 360°
360°- 310° = 50°

Question 10.
Find the measure of ∠c.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 10$
Answer: 294°
Explanation:
complete angle is 360°
given information
40°+ 26° = 66°
360°- 66° = 294°

Find the unknown angle measures.

Question 11.
Find the measure of ∠q.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 11$
Answer: 150°
Explanation:
complete angle is 360°
given information
90°+37°+ 83° = 210°
360°- 210° = 150°

Question 12.
Find the measure of ∠r.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 12$
Answer: 68°
Explanation:
complete angle is 360°
given information
90°+90°+ 112° = 292°
360°- 292° = 68°

Question 13.
Find the measure of ∠a.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 13$
Answer: 106°
Explanation:
complete angle is 360°
given information
90°+164° = 254°
360°- 292° = 106°

Question 14.
$\overleftrightarrow{P R}$ and $\overleftrightarrow{T U}$ meet at Q. Find the measures of ∠PQSand ∠TQR.
$Math in Focus Grade 5 Chapter 12 Practice 2 Answer Key Angles at a Point 14$
Answer:
m∠PQS = 54°
m∠TQR = 105°
Explanation:
complete angle is 360°
given information
∠PQT = 75° = ∠UQR
∠PQS = 180° – 51° + 75° = 54°
∠TQR = 180° – 75° = 105°