Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 2 Practice 1 Estimation to finish your assignments.
Math in Focus Grade 4 Chapter 2 Practice 1 Answer Key Estimation
Find each sum or difference. Then use rounding to check that your answers are reasonable. Round each number to the nearest hundred.
Example
534 + 287
534 + 207 = 021
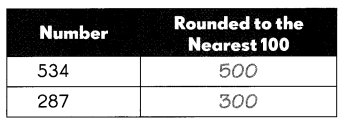
Add: 500 + 300 = 800
821 is close to 800.
So, the answer is reasonable.

Question 1.
515 + 342
Answer:
515 + 342=857
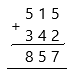
Now we added the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 515:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘1’.
– 1 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 500
The second number is 342:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘4’.
– 4 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 300.
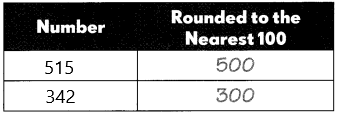
Now add both the numbers:
500+300=800
Therefore, the answer is not reasonable.
For the number 857, the round figure is 900 because in the tens place number ‘5’ is there. According to rule 2, +1 should be added to the hundreds place and the remaining places will become zero. Then it becomes 900. But here we got the estimated value of 800. That’s why it is not reasonable.
Question 2.
681 – 519
Answer:
681 – 519=162
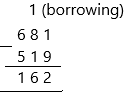
Explanation:
Now we subtracted the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 681:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘8’.
– 8> 5, +1 is added to the rounding digit (hundreds place) and the remaining places will become 0.
– The rounding off number is 700.
The second number 519:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘1’.
– 1 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 500
Now subtract both the numbers:
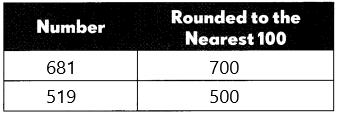
700-500=200
Therefore, the answer is reasonable.
168 is nearer to 200 according to rule 2.
Question 3.
170 + 725 + 333
Answer:
170 + 725 + 333=1228
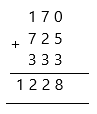
Explanation:
Now we added the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 170:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘7’.
– 7 > 5, +1 is added to the rounding digit (hundreds place) and the remaining places will become 0.
– The rounding off number is 200.
The second number is 725:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘2’.
– 2 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 700
The third number is 333:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘3’.
– 3 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 300.
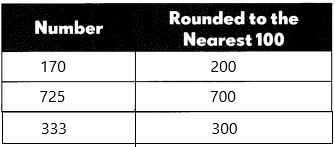
Now add all the three estimated numbers:
200+700+300=1200
Therefore, the answer is reasonable.
Question 4.
2,979 – 814
Answer:
2,979 – 814=2165
Explanation:
Now we subtracted the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 2,979:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘7’.
– 7 > 5, +1 is added to the rounding digit (hundreds place) and the remaining places will become 0.
– The rounding off number is 3000.
The second number is 814:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘1’.
– 1 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 800
Now subtract both the numbers:
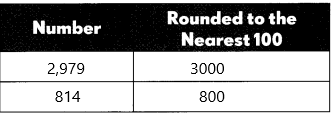
3000-800=2200
the answer is reasonable.
2,165 is nearer to 2,200.
Find each sum or difference. Then use front-end estimation to check that your answers are reasonable.
Example

Question 5.
7,930 + 2,517
Answer:
7,930 + 2,517=10,447
The answer is 10,447
Explanation:
Now we added the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 7,930:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘3’.
– 3< 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 7900.
The second number is 2,517:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘1’.
– 1 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 2500
Now add the estimated values:
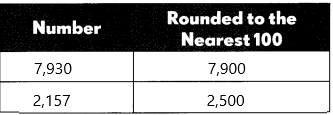
7900+2500=10400
10,447 is close to 10,400
So, the answer is reasonable.
Question 6.
3,166 – 1,625
Answer:
3,166 – 1,625=1541
the answer is 1,541.
Explanation:
Now we subtract the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 3,166:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘6’.
– 6> 5, +1 is added to the rounding digit (hundreds place) and the remaining places will become 0.
– The rounding off number is 3200.
The second number is 1,625:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘2’.
– 2 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 1600
Now subtract the estimated values:
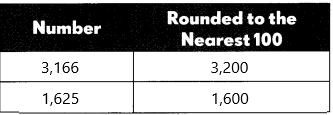
3,200-1,600=1,600
1541 is close to 1500, not 1600
So, the answer is not reasonable.
Question 7.
36,053 + 11,832
Answer:
36,053 + 11,832=47,885
The answer is 47,885
Explanation:
Now we add the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 36,053:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘5’.
– 5 = 5, +1 is added to the rounding digit (hundreds place) and the remaining places will become 0.
– The rounding off number is 36,100.
The second number is 11,832:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘3’.
– 3 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 11,800
Now add the estimated values:
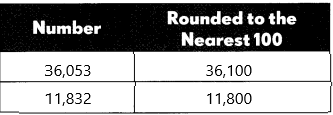
36,100+11,800=47,900
47,885 is close to 47,900
So, the answer is reasonable.
Question 8.
9,705 – 8,250
Answer:
9,705 – 8,250=1455
The answer is 1,455.
Explanation:
Now we subtract the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The first number is 9,705:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘0’.
– 0 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 9,700.
The second number is 8,250:
We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘5’.
– 5 <= 5, +1 is added to the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 8,300
Now subtract the estimated values:
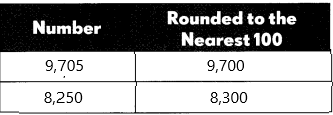
9,700-8,300=1,400
1,455 is close to 1,500, not 1,400
So the answer is not reasonable.
Find each product. Then use rounding to check that your answers are reasonable. Round the 3-digit number to the nearest hundred.
Example
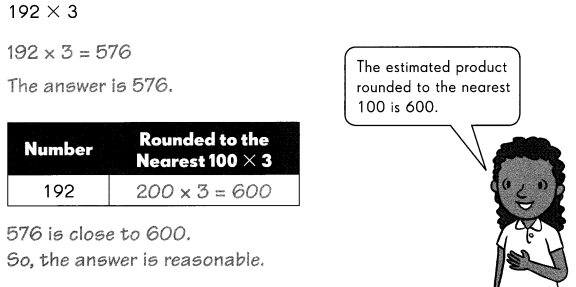
Question 9.
233 × 4
Answer:
233 × 4=932
The answer is 932
Explanation:
Now we multiply the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The number is 233:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘3’.
– 3 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 200.
Now multiply the estimated value by 4.
200 × 4 = 800
932 is not close to 800.
932 is close to 900
So, the answer is not reasonable.
Question 10.
485 × 2
Answer:
485 × 2 = 970
The answer is 970
Explanation:
Now we multiply the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The number is 485:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘8’.
– 8 > 5, +1 is added to the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 500.
Now multiply the estimated value by 2.
500 × 2 = 1000
970 is close to 1000.
So, the answer is reasonable.
Question 11.
117 × 5
Answer:
117 × 5 = 585
The answer is 585.
Explanation:
Now we multiply the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The number is 117:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘1’.
– 1 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 100.
Now multiply the estimated value by 5.
100 × 5 = 500
585 is not close to 500
585 is close to 600
So, the answer is not reasonable.
Question 12.
276 × 3
Answer:
276 × 3 = 828
the answer is 828
Explanation:
Now we multiply the above-given numbers.
We have to estimate the numbers and then add the estimated numbers to know the above result is correct or not.
In Maths, rounding numbers is a kind of estimating the numbers in the rounded form rather than the exact form. There are some procedures to round off the whole numbers. To round off whole numbers, find the place value that you want to round, and just see the digit just right to it.
RULE 1: If that digit number is less than 5, don’t change the rounding figure, but replace all the digits right to the rounding digits to “zero”.
RULE 2: If it is greater than 5, add 1 to the rounding digit, and replace all the digits right to the rounding digits to “zero”.
The number is 276:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘7’.
– 7 > 5, +1 is added to the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 300.
Now multiply the estimated value by 3.
300 × 3 = 900
828 is not close to 900
828 is close to 800
So, the answer is not reasonable.
Find each product. Then use front-end estimation to check that your answers are reasonable.
Example

Question 13.
108 × 3
Answer:
108 × 3 = 324
The answer is 324
Explanation:
Front end rounding is taking the number farther to the left and rounding it. So with our number, 108, we will be rounding to the hundreds since the farthest number to the left is a 1 and it’s in the hundredth place. The front end means the front or first digit in the number.
secondly, how do you round a number? Here’s the general rule for rounding:
1. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.
2. If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.
The number 108:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘0’.
– 0 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 100.
Now multiply the estimated value by 3.
100 × 3 = 300
324 is close to 300
So, the answer is reasonable.
Question 14.
121 × 5
Answer:
121 × 5 = 605
the answer is 605
Explanation:
Front end rounding is taking the number farther to the left and rounding it. So with our number, 121, we will be rounding to the hundreds since the farthest number to the left is a 1 and it’s in the hundredth place. The front end means the front or first digit in the number.
secondly, how do you round a number? Here’s the general rule for rounding:
1. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.
2. If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.
The number 121:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘0’.
– 2 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 100.
Now multiply the estimated value by 5.
100 × 5 = 500
605 is close to 600, not 500
So, the answer is not reasonable.
Question 15.
439 × 2
Answer:
439 × 2 = 878
the answer is 878
Explanation:
Front end rounding is taking the number farther to the left and rounding it. So with our number, 439, we will be rounding to the hundreds since the farthest number to the left is a 4 and it’s in the hundredth place. The front end means the front or first digit in the number.
secondly, how do you round a number? Here’s the general rule for rounding:
1. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.
2. If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.
The number 439:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘0’.
– 3 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 400.
Now multiply the estimated value by 2.
400 × 2 = 800
878 is close to 800
So, the answer is reasonable.
Question 16.
227 × 4
Answer:
227 × 4 = 908
the answer is 908.
Explanation:
Front end rounding is taking the number farther to the left and rounding it. So with our number, 439, we will be rounding to the hundreds since the farthest number to the left is a 4 and it’s in the hundredth place. The front end means the front or first digit in the number.
secondly, how do you round a number? Here’s the general rule for rounding:
1. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.
2. If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.
The number 227:
– We need to round off nearest to hundred so check the tens place.
– The tens place is having the digit ‘2’.
– 2 < 5, we don’t change the value of hundreds of places and the remaining places will become 0.
– The rounding off number is 200.
Now multiply the estimated value by 4.
200 × 4 = 800
908 is not close to 800
So, the answer is not reasonable.
Find each quotient. Then use related multiplication facts to check that your answers are reasonable.
Example
85 ÷ 5
85 ÷ 5 = 17
The answer is 17.
since division is the opposite of multiplication, find a multiple of 5 that is close to 8.

5 × 10 = 50
5 × 20 = 100
85 is closer to 100 than to 50.
So, 85 ÷ 5 rounds to 100 ÷ 5.
100 ÷ 5 = 20
85 ÷ 5 is about 20.
17 is close to 20.
Answer 17 is reasonable.
Question 17.
78 ÷ 2
Answer:
78 ÷ 2 = 39
The answer is 39
since division is the opposite of multiplication, find a multiple of 2 that is close to 78.
2 × 20 = 40
2 ×30 = 60
2 × 40 = 80
78 is closer to 80
so, 78 ÷ 2 rounds to 80 ÷ 2
80 ÷ 2 = 40
78 ÷ 2 is about to 40.
39 is close to 40
Answer 39 is reasonable.
Question 18.
68 ÷ 4
Answer:
Solve. Decide whether to find an estimate or an exact answer.
Example
Danny and his 3 friends buy baseball tickets for $26 each. About how much money do they need altogether?
Because the question asks ‘about how much money they need, you can estimate.

4 × $30 = $120
They need about $120.
Question 21.
Jonathan, Shia, and Casey bought 35 toy figures. Each of the boys decides to make a team of 11 figures. Do they have enough toy figures?
Answer: yes
Explanation:
The number of toys figures they bought=35
The number of figures they want to decide to make a team=11
Now the above-given question was asked do they have enough toy figures=?
If we go for the estimation process:
35 is close to 40
11 is close to 10
If we divide both the numbers then we get the estimated answer which is close to the original answer.
The original answer:
35/11=3.18
Now do the estimation process:
40/10=4
3.18 is close to the 4.
So, the answer is reasonable.
Question 22.
A turtle hatchery collected 457 turtle eggs in a week. The next week, it collected 656 eggs. About how many eggs did the hatchery collect in the two weeks?
Answer:
The number of turtle eggs a title hatchery collected in a week=457
The number of turtles eggs a title hatchery collected in a next week=656
The number of turtle eggs he collected in two weeks=X
X=457+656
X=1113
Therefore, he collected 1113 eggs in two weeks.
Question 23.
The table shows the number of beads in Stella’s collection.
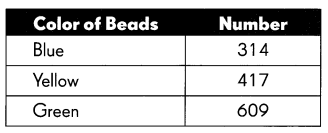
Stella needs 400 yellow beads, and 700 green beads to make a necklace. Does she have enough beads for the necklace?
Answer: yes, she could have enough beads.
The number of yellow beads Stella needs=400
The number of green beads Stella needs=700
In the above-given figure, the number of colours of beads is given.
But in the question, green beads are more than yellow beads. Moreover, the question asked was yellow and green beads are given. So according to that, we calculate the beads.
In the above-given figure:
Yellow beads=417
Green beads=609
The total number of beads=1026
In the question given:
Yellow beads=400
Green beads=700
The total number of beads=1100
So, definitely she can make necklace with the given number of beads.
Read More: