Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 6 Fractions and Mixed Numbers to score better marks in the exam.
Math in Focus Grade 4 Chapter 6 Answer Key Fractions and Mixed Numbers
Math Journal
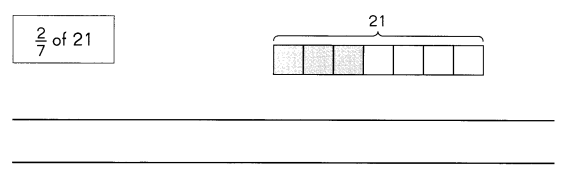
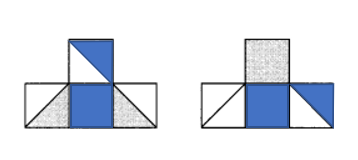
Is the model correct? If not, explain why it is wrong. Draw the correct model.
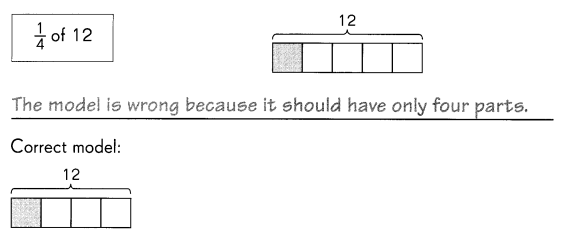
Correct model:
Answer:
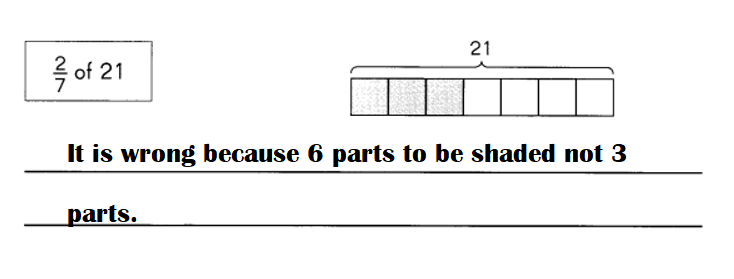
Explanation:
(2 ÷ 7 ) × 21 is wrong because 6 parts should be shaded not 3.
(2 ÷ 7 ) × 21 = 2 × 3 = 6.
Put On Your Thinking Cap!
Challenging Practice
Question 1.
Show 1\(\frac{1}{4}\)– shaded, if 1 whole is made up of 4 squares. Some of the shading has been done for you.
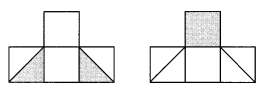
Answer:
Explanation:
1\(\frac{1}{4}\) of 4
= (5 ÷ 4) × 4
= 5.
Question 2.
Is the answer of 21 × \(\frac{2}{7}\) the same as that of 2 × \(\frac{21}{7}\)? Show your work.
Answer:
Yes, both the answers are same.
Explanation:
21 × \(\frac{2}{7}\) = 3 × 2 = 6.
2 × \(\frac{21}{7}\) = 2 × 3 = 6.
Question 3.
Write a fraction and a whole number that have the same product as the problem below.
8 × \(\frac{3}{4}\) = ___
____ × _____ = ___
Answer:
8 × \(\frac{3}{4}\) = 3 × \(\frac{8}{4}\) = 3 × 2 = 6.
Explanation:
8 × \(\frac{3}{4}\) = 2 × 3 = 6.
3 × \(\frac{8}{4}\) = 3 × 2 = 6.
Put On Your Thinking Cap!
Problem Solving
Caroline places five poles A, B, C, D, and E in order along a straight line. The distance between poles A and D is 1 yard. The distance between poles B and C is the same as the distance between poles A and B.
Poles A and B are \(\frac{1}{5}\) yard apart.
The distance between D and E is \(\frac{7}{10}\) yard.
How far apart are poles B and E?
Answer:
Distance between poles B and E = 3 ÷ 2 or \(\frac{3}{2}\).
Explanation:
Distance between poles A and D = 1 yard.
The distance between poles B and C is the same as the distance between poles A and B.
=> Distance between poles B and C = Distance between poles A and B.
Let the distance between poles B and C be X.
Distance between poles A and B = \(\frac{1}{5}\) yard.
Distance between poles D and E = \(\frac{7}{10}\) yard.
Distance between poles A and B + Distance between poles B and C + Distance between C and D = Distance between poles A and D
= \(\frac{1}{5}\) + \(\frac{1}{5}\) + Distance between C and D = 1
= \(\frac{2}{5}\) + Distance between C and D = 1
= Distance between C and D = 1 – \(\frac{2}{5}\)
= Distance between C and D = (5 – 2) ÷ 5
= Distance between C and D = 3 ÷ 5 or \(\frac{3}{5}\) yard.
Distance between poles B and E = Distance between poles B and C + Distance between C and D + Distance between poles D and E
= \(\frac{1}{5}\) + \(\frac{3}{5}\) + \(\frac{7}{10}\)
= \(\frac{4}{5}\) + \(\frac{7}{10}\)
= (8 + 7) ÷ 10
= 15 ÷ 10
= 3 ÷ 2 or \(\frac{3}{2}\)